浅吃水超大型浮体连接器动力响应

刘 超，祁恩荣，陆 晔

（中国船舶科学研究中心，江苏 无锡 214082）

浅吃水超大型浮体连接器动力响应

刘 超，祁恩荣，陆 晔

（中国船舶科学研究中心，江苏 无锡 214082）

采用刚性模块柔性连接器（RMFC）模型，柔性连接器假定为线性弹簧模型。基于三维势流理论计算浮体水动力，从而得到连接器的动力响应。计算并比较了3种不同模型在7级海况作用下的连接器动力响应，研究了浅水效应对连接器动力特性的影响，得到超大型浮体连接器动力响应一定的规律，从而为浅吃水超大型浮体连接器的设计提供一定的参考。

VLFS；RMFC；浅吃水；连接器载荷

1 引 言

近年来，随着海洋资源的开发和利用，越来越多的超大型浮体被广泛应用，如日本的海上浮式机场Mega-Float和美国的海上移动基地MOB。超大型浮体，一般是指那些尺度以公里计的浮式海洋结构物，以区别于目前尺度以百米计的船舶和海洋工程结构物，如海洋平台等。由于超大型浮体的巨大，注定它不可能是一个无间断单体，否则中拱或中垂变形会使结构受力十分巨大。为了减小结构剖面上较高的载荷，一般将浮体分成若干个模块，采用连接器相连，且允许模块间的某些相对运动。

目前国内外研究浮体连接器的文献不多，研究浅吃水浮体连接器的相关文献则更少。Ertekin（1993）[1]利用三维势流理论和格林函数法并考虑了刚体模块间水动力相互影响，计算了MOB模块的运动和连

接器载荷。吴有生（1995）[2]利用三维线性水弹性理论，研究了弹性连接多刚体模块系统的流固耦合问题，得到了结构在不同浪向角下的运动和变形以及连接件动力响应。Riggs（1998）[3]仍采用上述计算方法，计算了单模块、不相连的5模块、柔性连接的5模块以及刚性连接的5模块MOB的运动和连接器载荷。王璞（2002）[4]用Airy波来模拟工作海况，用Morrison公式计算波浪载荷，采用一种时间序列法分析了三模块半潜式浮体连接器的动力特性。余澜（2003）[5-7]采用三维线性水弹性理论，分析了MOB模块间相互作用力、连接器刚度、浪向角、海况对模块运动和连接器载荷的影响。余建星（2006）[8-9]采用有限水深三维势流理论计算水动力，分析了浪向角改变对栈桥码头运动响应的影响，并将谱分析结果与实验结果进行了比较，为连接器及锚链设计提供依据。上述文献，对多浮体连接器分析方面，具有很重要的理论和实践意义。本文以3个不同浮体模型为算例进行分析，主要讨论浅吃水浮体连接器载荷的动力特性。

2 理论概述

2.1 水动力系数

假定有n个无航速作小幅简谐运动的浮体，各浮体之间具有一定的间隙，流场总速度势为：式中：φI和φD分别为入射势和绕射势，为浮体k的j模态运动的复数响应幅值，对应于各浮体的纵荡（surge）、横荡（sway）、垂荡（heave）、横摇（roll）、纵摇（pitch）和艏摇（yaw）。为系统中其它浮体固定不动，仅有浮体k的j模态单位幅值运动引起的速度势，称为浮体系统中浮体k的j模态规范化速度势。

绕射势φD和浮体k的规范化速度势应满足Laplace方程、自由表面条件、各浮体的物面条件、海底条件和无穷远处辐射条件。

2.2 连接器作用力

两个浮体之间用两个连接器相连，n个浮体之间就有2（ n- ）1 个连接器，本文假定各连接器为线性弹簧模型，即适当限制三个方向的线位移，允许三个方向上的角位移。假设连接器i位于浮体k上，则i连接点的运动表达式为：

式中：i=1，2，…，2×（n- ）1 ；Ni第i个连接器连接点的位移函数矩阵。

连接器的载荷与变形符合线性虎克定律，因此由两个相邻浮体的运动而引起的连接器变形所产生的作用力可表示为：

式中：Kc为连接器的弹簧刚度矩阵；Δul，l+1表示相邻两个浮体l、1+1运动在连接点处所产生的位移差，l=1，2，…，n-1。

式中：i和j分别为位于第l和l+1浮体上的连接器连接点位置。

浮体l、l+1之间的连接器所得到的刚度矩阵在整体坐标系下可以表示为：

因此，所有连接器组成的连接器的总刚度矩阵Ks可以表示为：

式中：Ks为所有连接器组成的总刚度矩阵（6N×6 ）N 。

2.3 多浮体运动方程

把水动力系数和连接器作用力代入多浮体动力学方程，得到频域运动方程：

3 计算模型参数

计算模型由5个相同浮体、8个连接器组成。浮体用M1～M5表示，连接器用C1～C8表示，见图1。每个浮体关于xioiyi平面和yioizi平面对称。模块之间用2个连接器连接，连接器位于模块上体甲板处，关于xi轴对称。连接器为线性弹簧模型，适当限制三个方向的线位移，允许三个方向上的角位移。

图1 多浮体系统示意图Fig.1 Coordinate system of multi floating structure

表1为单个浮体的设计参数。上体的长度是指单浮体的首部至尾部的长度，不包括连接器的长度。连接器的长度为25 m。Ixx、Iyy和Izz分别表示单个模块在各自局部坐标系下分别以oixi、oiyi和oizi为轴旋转得到的质量矩。模型1参考了美国MOB设计方案，为了适应近岸浅吃水浮体的设计，我们在模型1的基础上，进行改进，依次减小了型深和设计吃水，设计了模型2和模型3。设计水深为300 m。

表1 单个浮体的设计参数Tab.1 Property of single floating structure

本文计算了 8 个浪向角（0°、15°、30°、45°、60°、75°、85°和 90°）、36 个频率（0.1～1.5 Hz）规则波下，12种不同连接器刚度时的浮体运动和连接器载荷。并进行了7级海况下的短期预报，分析了浮体不同吃水深度对连接器载荷的影响。

本文选取了12种不同的连接器刚度，连接器刚度从小到大排列。为了方便比较，在下文中列出了连接器X、Y和Z方向的刚度值，连接器的选择是从柔软到坚硬。连接器刚度如表2所示。

表2 连接器刚度表（N/m）Tab.2 List of connector stiffness

本文短期预报选取的波浪谱为Bretschneider谱，Bretschneider谱密度表达式如下：

式中：ω为入射波频率，Hs为特征波高，Tp为谱峰周期。西北太平洋7级海况的特征波高取为7.5 m，谱峰周期取为13.8 s，短期预报取为千分之一响应均值。

4 结果分析

4.1 连接器动力特性分析

本文分别计算了三个浮体模型，在12种不同连接器刚度时的载荷值，并进行了载荷最大值短期预报。

通过图2，我们可以发现：（1）连接器刚度对连接器最大载荷的影响比较明显，连接器最大载荷随着连接器刚度的变化发生明显的变化，特别是最大纵向载荷。连接器最大载荷在某些刚度时会急剧增大，但当刚度增加到一定值后则逐渐趋于平稳。（2）在同一刚度处，三个模型的最大载荷差距较大，特别是最大纵向载荷。当刚度较大载荷趋于平稳时，模型1的最大纵向载荷、最大横向载荷大于模型2和模型3，最大垂向载荷大于模型2但却小于模型3。

出于连接器刚度的选择原则：既要使连接器载荷适中，还要使各个模块运动响应适中。因此，我们暂定K10为连接器设计刚度。为了进一步研究模型3最大垂向载荷增大的原因，我们以连接器刚度K10为例，对其不同浪向角载荷最大值进行短期预报。

由图3我们可以看到，在K10刚度时，连接器载荷最大值都出现在85°浪向角。模型1连接器最大纵向载荷、最大横向载荷在不同浪向角下都要大于模型2和模型3，最大垂向载荷在不同浪向角下都要大于模型2但却小于模型3。图4以模型1和模型3在K10刚度85°浪向角和90°浪向角为例，分析它们的载荷—频率曲线。

图2 不同刚度连接器载荷最大值Fig.2 Max connector loads of different stiffness

对比上述几图，我们可以看到：（1）在低频区和高频区，模型1和模型3连接器载荷都比较小，两者相差不大，几乎一致；但在中频区，即波浪能量集中频率区，模型1和模型3连接器载荷都较大，模型1连接器纵向载荷、横向载荷明显大于模型3，但垂向载荷却明显小于模型3。（2）85°浪向角时，连接器载荷峰值区非常大，且主要集中分布在中频区；而90°浪向角时，连接器载荷峰值区非常小，且峰值远小于85°浪向角时的峰值。所以85°浪向角时连接器最大载荷会大于90°浪向角时连接器最大载荷。

图3 不同浪向角连接器载荷最大值（K10）Fig.3 Max connector loads of different wave angle(K10)

图4 模型1和模型3连接器载荷Rao比较（85°，90°）Fig.4 Comparison of Rao of connector loads of Model1 and Model3(85°,90°)

由（8）式和（9）式我们知道，在连接器刚度和位置确定的情况下，连接器的纵向载荷与浮体间的相对纵荡、纵摇和艏摇密切相关，横向载荷与浮体间的相对横荡、横摇和艏摇密切相关，垂向载荷与浮体间的相对垂荡、横摇和纵摇密切相关。下面我们以连接器K10刚度85°浪向角和90°浪向角为例，对比分析模型1和模型3浮体的运动。

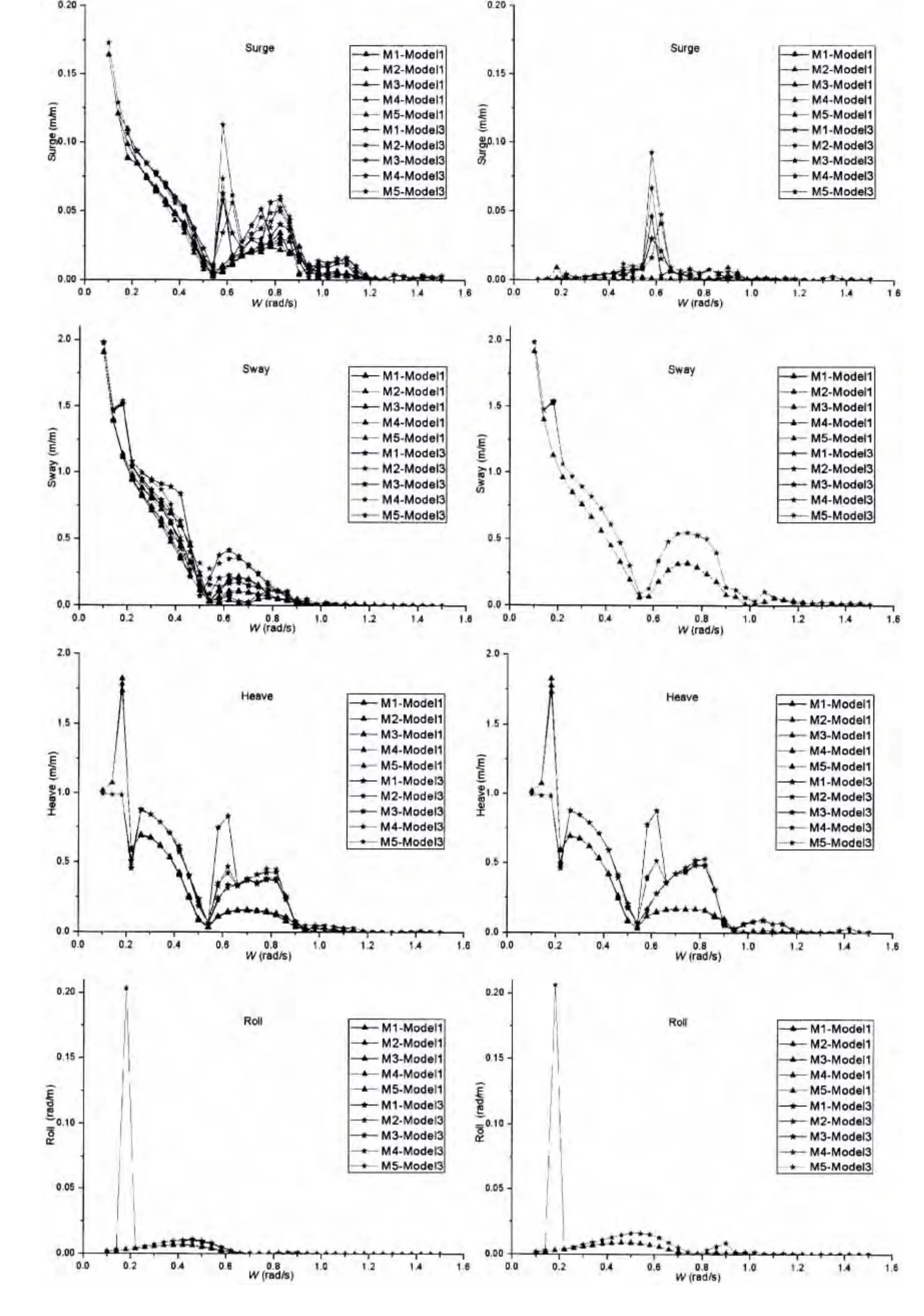
通过上述几图对比，我们可以发现：（1）在低频区和高频区，模型1和模型3模块相对运动都比较小，所以连接载荷较小；在中频区，模型1和模型3模块某些相对运动都增大，所以连接载荷增大。模型3模块相对垂荡和纵摇运动明显大于模型1，所以模型3连接器的垂向载荷会大于模型1。（2）85°浪向角时浮体间的相对运动都要大于90°浪向角时，特别是相对纵荡和纵摇，所以85°浪向角时连接器载荷会大于90°浪向角时连接器载荷。

由3.1节单个浮体设计参数，我们可以知道：模型1、模型2和模型3的长度、型宽、质量分布和连接器安装位置几乎一样，但型深、重心和吃水等不相同，具体见表3。相比模型1，模型2和模型3排水量更小、型深更小，吃水更浅，更符合近岸浮体的特点。

表3 三个模型的比较Tab.3 Comparison of the three models

我们发现：相比与模型1，模型2和模型3相对吃水减小，相对浮心降低，而三个模型的相对重心相差不大，模型2要稍微小一些。因此，模型3的相对重心浮心差大于模型1和模型2，从而导致模型3的恢复力矩较小，稳性较差。

通过以上分析，我们可以得到：相比模型1，模型3由于相对重心浮心差较大，恢复力矩较小，稳性较差，模块间的相对垂荡、相对纵摇增大，从而导致连接器的垂向载荷增大。

4.2 浅水效应分析

近岸浅吃水超大型浮体由于工作水域水深有限，有限水深带来的浅水效应必然会影响浮体的运动和连接器载荷。为了研究浅水效应对浮体连接器动力特性的影响，本小节计算了模型3在50 m设计水深时浮体连接器的载荷，并与前面300 m设计水深时的连接器载荷进行了对比分析。

与4.1节一样，计算不同刚度连接器在7级海况下的载荷预报最大值，见图6。

我们可以看到：相比300 m水深，50 m水深时连接器纵向最大载荷值在刚度K4、K5和K6处增幅比较明显，其它刚度处增幅则较小，且两者的变化趋势一样。所以，浅水效应会导致连接器最大载荷值增大，但并不会改变连接器刚度的选择，依然选择K10为设计刚度。

计算K10刚度连接器在7级海况下不同浪向角的载荷短期预报最大值，见图7。

我们发现：50 m水深与300 m水深两者连接器的变化规律几乎一样，在85°浪向角最大载荷处，50 m水深连接器最大载荷稍微大于300 m水深连接器最大载荷。

我们继续分析50 m水深与300 m水深时连接器的载荷频率曲线，以连接器出现最大载荷时的浪向角—85°浪向角为例，详见图8。

分析上述几图，我们发现：50 m水深与300 m水深时连接器的载荷频率曲线几乎一致，50 m水深连接器载荷较300 m水深连接器载荷稍微有所增大。

图6 不同刚度连接器最大载荷值（SS7）Fig.6 Max connector loads of different stiffness

图7 连接器最大载荷值（K10）Fig.7 Max connector loads of different wave angle(K10)

图8 模型3连接器载荷Rao比较（50 m，300 m）Fig.8 Comparison of Rao of connector loads of Model3(50 m,300 m)

通过以上分析，我们可以得到：浅水效应的确会导致连接器最大载荷增大，但并不会影响连接器刚度的选择。浅水效应引起连接器在设计刚度处载荷增加的幅度不大，影响不明显。

5 结 论

通过上述分析，本文可以得到以下结论：（1）相比于深吃水超大型浮体，浅吃水超大型浮体的重心浮心差较大，恢复力矩较小，稳性较差，模块间的相对垂荡、相对纵摇增大，从而导致浮体间连接器的垂向载荷增大。因此，对于浅吃水超大型浮体连接器的设计，一定要特别注意降低结构重心，否则会引起连接器垂向载荷的增加。（2）浅水效应的确会导致连接器最大载荷增大，但并不会影响连接器刚度的选择。浅水效应引起连接器在设计刚度处载荷增加的幅度不大，影响不明显。（3）85°浪向角时由于浮体间的相对运动大于90°浪向角时，特别是相对纵荡和纵摇，所以85°浪向角时连接器载荷会大于90°浪向角时连接器载荷。

本文研究受到国家重点基础研究发展（973）计划项目海洋超大型浮体复杂环境响应与结构安全性（2013CB036100）和国防预研支撑项目（6401010103）的资助。

[1]Ertekin R C,Riggs H R,Che X L.Efficient methods for hydroelastic analysis of very large floating structure[J].Journal of Ship Research,1993(1):58-76.

[2]吴有生,杜双兴.极大型海洋浮体结构的流固耦合分析[J].舰船科学技术,1995(1):1-9.

[3]Riggs H R,Ertekin R C,Mills T R J.Wave-induced response of a 5-module mobile offshore base[C].Mechanics and Arctic Engineering,OMAE,1998.

[4]王 璞,余 澜,李润培.半潜式超大浮体模块连接器动力特性的一种时间序列分析方法[J].海洋工程,2002,20(3):9-13.

[5]余 澜,李润培,舒 志.移动式海上基地连接器的动力特性[J].上海交通大学学报,2003,37(8):1159-1163.

[6]余 澜,丁 伟,李润培.移动式海上基地多模块间相互作用对连接器载荷的影响[J].海洋工程,2004,22(1):25-31.

[7]Yu Lan,Li Runpei,Shu Zhi.Dynamic responses of mobile offshore base connectors[J].China Ocean Engineering,2003,17(4):469-479.

[8]余建星,苏春华.近海移动式栈桥码头运动性能计算方法[J].中国港湾建设,2006(6):14-17.

[9]余建星,董文斌,戴愚志.RMFC模型在新型拼接式海上栈桥码头三维运动响应计算中的应用[J].海工技术,2006(4):1-4.

Dynamic response of connectors of Very Large Floating Structures under shallow draft

LIU Chao,QI En-rong,LU Ye
(China Ship Scientific Research Center,Wuxi 214082,China)

The rigid module flexible connector model is applied,the flexible connectors are modeled as linear springs.Three-dimensional potential flow theory is adopted to calculate hydrodynamic forces and dynamic response of connectors.The dynamic response of connectors in 3 different models under sea state 7 is analyzed and compared,and the shallow water effect on dynamic characteristics of connectors is studied,which can provide guides for the design of connectors of very large floating structures under shallow draft.

VLFS(very large floating structures);RMFC(rigid module flexible connector);shallow draft;connector loads

U661.4

A

10.3969/j.issn.1007-7294.2014.05.013

1007-7294（2014）05-0581-10

2014-01-22

国家重点基础研究发展（973）计划项目（2013CB036100）和国防预研支撑项目（6401010103）

刘 超（1990-），男，中国船舶科学研究中心硕士生，E-mail：chaoliuhust@gmail.com；

祁恩荣（1965-），男，中国船舶科学研究中心研究员。