涉及重整化变换的有理函数族的Fatou集

高军杨，马庆文

(中国矿业大学(北京)理学院，北京100083)

0 引言与主要结论

平衡统计力学的主要任务是解释相与相变的本质［1］.统计力学中的 Yang-Lee 理论［2-3］把自由能量拓广为复温度的函数，继而把物理相位的概念描述为它的解析区域.这些区域的边界是自由能量的奇点.因此，研究自由能量的奇点在复平面上的分布以及整体结构就成为一个重要的问题.然而，自Yang-Lee理论提出以来，这些区域的拓扑结构很少为人们所了解.考虑类金刚石型等级晶格上λ-态Potts模型，文献［4-5］证明了其配分函数零点的极限集合就是经过重整化变换后的有理映照族Tnλ的Julia集 J(Tnλ).这里

其中n＞1是同所考虑的类金刚石型等级晶格的分叉度相关联的自然数，J(Tnλ)是Tnλ的斥性周期点集的闭包，Fatou集F(Tnλ)即为复球面上 J(Tnλ)的余集.因此，对重整化变换J(Tnλ)的Fatou集和Julia集的拓扑性质进行研究，不仅在复动力系统中有重要的理论意义，而且对统计力学也有重要的应用价值.首先，称单连通区域G是John区域是指:存在常数M1＞ 0，使得∀a，b∈∂G且直线段［a，b］⊆G，满足

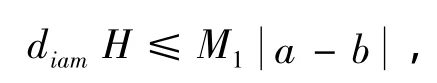
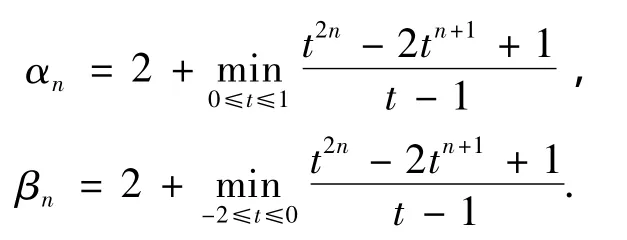
定理1Tnλ(z)如(1)式定义，则有如下结论:

(i)若 λ ∈ R{αn，βn}，则 Tnλ的每个 Fatou分支都是John区域;

(ii)若λ= αn，则Tnλ存在抛物不变域Lαn(q)，其任意的逆象分支都是 John区域，但Tnαn其它的Fatou分支都不是John区域;

(iii)若 λ= βn，则当 n 为偶数时，Tnβn的每个Fatou分支都是John区域;当n为奇数时，除了超吸性不变域Aβn(∞)及其任意的逆象分支(k=1，2，…)不是 John 区域外，Tnβn的其它 Fatou分支都是John区域.

1 预备知识

对于涉及上述定义的经典复动力学结论，可参见文献［7-9］.

由于学生之间存在差异性和多样性，在学习过程中，每个学生具有其特有的意义构建过程。所以，教师不仅要对学生的学习进行管理，更重要的是必须对不同学生进行不同的学习引导，启发每位学生的创新思维。作为学生学习的引导者，教师在执行角色时的行为特征表现在：在审阅每位学生介绍材料的基础上，提出问题，组织学生进行思考和讨论，在讨论中引导学生，启发诱导他们自己去发现规律，同时对自身错误或片面的认识进行纠正或补充，从而加深学生对教学内容的理解；尽量给每位学生同等参与讨论的机会，经常了解学生的意见，随时修正自己在期望值上的偏差。最重要的是，相信每位学生都有学习的潜力，给每位学生创新的机会，引导学生不断地向目标迈进。

定义2［5］若α∈J(f)，如果∃p(＜∞)对互不相同的光滑弧它们仅在处相交，γj与在α点相切，而当i≠ j时，γj与在α点不相切.当δ＞ 0 充分小时，把Δδ(α)(γj∪)较小的那个分支记为Lj(δ)，称之为γj和的尖角域.如果δ充分小，

则称α为具有p个花瓣的花核点，仅有1个花瓣的花核点就是Julia集J(f)的1个尖点.这里，Δδ(α)=

引理1 若f是临界非回归的有理函数，则Λ(f)≠Λ0(f)当且仅当J(f)为圆周、圆弧或者有限条互不交解析弧上的Cantor集.

引理2［10］若f是半双曲的有理映照，则f的每个Fatou分支都是John区域.

2 定理的证明

为证明定理1，先证明下面的2个引理.

引理3 若 λ= αn，则 Tnαn存在抛物不变域Lαn(q)，其任意的逆象分支都是John区域，但Tnαn的其它Fatou分支都不是John区域.

证(i)注意到α2=0且T20(z)=(z+1)2/4，T'20(z)=(z+1)/2，T20仅有1个有限的临界点z=-1.显然，z=1是T20的抛物不动点，且当x∈［-1，1)时，0≤T20(x)＜T20(1)=1.另一方面，∀x∈［0，1)有T20(x)＞ x，并且当k→+∞ 时1.因此，［-1，1)⊂F(T20).记抛物不动点z=1的直接抛物域为L0(1).因为T20-1(0)={-1}⊆L0(1).所以L0(1)是F(T20)的完全不变域.易见F(T20)由2个完全不变域L0(1)和A0(∞)组成.因此，抛物不动点1处仅有1个抛物吸性花瓣.由Leau-Fatou花瓣定理知，抛物完全不变域L0(1)在抛物不动点1处与实轴R的夹角是2π.即z=1是抛物完全不变域L0(1)的内部尖点，从而L0(1)是John区域.因此z=1是∂A0(∞)的外部尖点，故A0(∞)不是John区域.显然，引理3的结论成立.

(ii)当n(＞2)为偶数时，由文献［5］中的命题6.2知，Tnαn仅有3个实不动点q1，1，q2(0＜ q1＜ 1＜q2).由文献［5］中定理6.16的证明知，Aαn(∞)是单连通完全不变域，故Tnαn的每个Fatou分支都是单连通区域.易见［1-λ/2，+∞)⊂Aαn(∞)，并且当，因此q1是吸性或抛物不动点.易证Tnαn在(q1，1)上是严格单调递增的且Tnαn(x)＞x，注意到z=1是吸性不动点，从而(q1，1］⊂Aλ(1).这说明q1是抛物不动点并且在q1处仅有1个抛物吸性花瓣.由于Aαn(∞)包含3个临界点1-λ/2，1-λ，∞，临界点收敛于抛物不动点q1，1 ∈Aλ(1)，故F(Tnαn)仅有3个周期域Aαn(1)，Aαn(∞)和 Lαn(q1).

由定义2可知，抛物不动点q1是Julia集J(Tnαn)上的尖点.再由Leau-Fatou花瓣定理知，抛物不变域Lλ(q1)在q1处与实轴R的夹角是2π.因此，q1是抛物不变域Lαn(q1)的内部尖点.由引理1知，q1的所有逆象点也是 J(Tnαn)上的尖点.易见Tnβn的临界点都在Fatou集F(Tnαn)中.既然Tnαn在q1的每1个逆象点的充分小的邻域内是共形的，所以都是内部尖点.因此，Lαn(q1)是 John区域.由 Riemann-Hurwitz公式

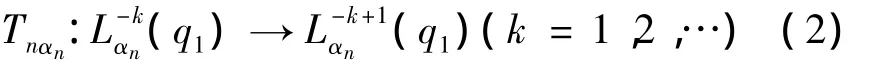
(iii)当n(＞2)为奇数时，完全类似于n为偶数的情况，可证 F(Tnαn)仅有3个周期域Aαn(1)，Aαn(∞)和Lαn(q2)，其中抛物不变域Lαn(q2)及其逆象分支都是John区域，但Aαn(1)和Aαn(∞)及它们的逆象分支都不是John区域.引理3得证.

引理4 若λ= βn'，则

(i)当n为偶数时，Tnβn的每个Fatou分支都是John区域;

(ii)当n为奇数时，Tnβn的每个Fatou分支都是John区域，除了超吸性不变域Aβn(∞)及其任意的逆象分支都不是 John 区域.

证(i)当n为偶数时，由文献［5］中定理6.16的证明知，Tnβn仅有3 个实不动点 q1，1，q2(0＜ q1＜1＜q2)，且q1是抛物不动点与抛物不变域Lβn(q1)单连通完全不变域.注意到Lαn(q1)，则 F(Tnβn)仅 有 3 个 周 期 域Aβn(1)，Aβn(∞)和 Lβn(q1).易见(q*12，q2)⊂Aβn(1)，这里，是斥性不动点q在区间(1-λ/2，1)的1个逆2像，并且⊂Aβn(∞)，这里是斥性不动点q2在区间(-∞，1-λ)的1个逆像.由文献［5］中的定理8.22的结论(也可以见文献［11］)，易见Aβn(1)，Aβn(∞)都是Jordan区域并且它们都关于实轴R对称.所以∂Aβn(1)R∪{∞}.所以，q1和它的任意逆象点(k=1，2，…)都不在 ∂Aβn(1)和 ∂Aβn(∞)上.

显然，Tnβn是临界非回归的有理函数，并且J(Tnβn)= ∂Lβn(q1).易证在抛物不动点 q1处仅有1个抛物吸性花瓣.由引理1知，抛物不动点q1和它的逆象点都是 Julia集 J(Tnβn)上的尖点，考虑到F(Tnβn) 仅 有 3 个 周 期 域Aβn(1)，Aβn(∞) 和Lβn(q1)，从而除了抛物不动点q1和它的所有逆象点之外，J(Tnβn)上不再存在其它的尖点.再由Leau-Fatou花瓣定理知，抛物完全不变域Lβn(q1)在q1处与实轴R的夹角是2π.因此，q1是抛物完全不变域Lβn(q1)的内部尖点.完全类似于引理3的讨论，能够得到q1的所有逆象点…)也是 J(Tnβn)上的内部尖点.因此，Lβn(q1)是John区域.由于 q1和它的所有逆象点都不在∂Aβn(1)和 ∂Aβn(∞)上，所以Aβn(1)和Aβn(∞)都是John区域.显然q1和它的所有逆象点都不在Aβn(1)和Aβn(∞)的逆象分支与上.因此，这些逆象分支也都是John区域.所以当 n为偶数时，Tnβn的每个Fatou分支都是John区域.

(ii)当n为奇数时，由文献［5］中定理6.16的证明知，Tnβn仅有 3 个实不动点 q1，1，q2(q1＜ -1，q2＞ 1)且q1是抛物不动点.(q1，1-λ］⊂Lβn(q1)，［1-λ/2，+∞］∩Lβn(q1)= ∅并且F(Tnβn)仅有3 个单连通的周期域Aβn(1)，Aβn(∞)和 Lβn(q1).易见(-∞，q1)∪(q2，+∞)⊂Aβn(∞)，q2是斥性不动点，则q1∈∂Aβn(∞)，从而在抛物不动点q1处仅有1个抛物花瓣.易证Tnβn在(1-λ/2，1)上是严格单调递增的且 Tnβn(x)＞ x，Tnβn在(1，q2)上是严格单调递增的，且注意到z=1是吸性不动点，因此，其中是q2在区间(1-λ/2，1)内的逆象，由文献［5］中的定理8.22的结论知道，Tnβn的每个Fatou分支都是Jordan区域，并且它们都关于实轴R对称.故q2}，所以，q1和它的所有逆象都不在∂Aβn(1)上.

显然，Tnβn是临界非回归的有理函数，并且J(Tnβn)显然不是圆周、圆弧或者有限条互不交解析弧上的Cantor集，由定义2与引理1知，抛物不动点q1和它的所有逆象点都是J(Tnβn)上的尖点，考虑到F(Tnβn) 仅 有 3 个 周 期 域Aβn(1)，Aβn(∞) 和Lβn(q1).因此，除了抛物不动点q1和它的所有逆象点之外，J(Tnβn)上不再有其它的尖点.再由Leau-Fatou花瓣定理知，抛物不变域Lβn(q1)在q1处与实轴 R的夹角是2π.因此，q1是抛物不变域Lβn(q1)的内部尖点.既然Tnβn在q1的充分小的邻域内是共形的，则q1的所有逆象点也是Lβn(q1)的内部尖点.因此，Lβn(q1)是John区域.完全类似于(2)式的讨论，能够推出 Lβn(q1)的所有逆像分支都是 John 区域.因为 q和它1的逆象都不在 ∂Aβn(1)上.所以，∂Aβn(1)上没有任何尖点.因此，Aβn(1)是 John区域.显然，q1和它的逆象都不在Aβn(1)的逆象分支上，故这些逆象分支也都是 John区域.因为 q1∈ ∂Aβn(∞)，故 q1是Aβn(∞)的外部尖点.由于John区域没有外部尖点，所以Aβn(∞)不是John区域.既然q1的逆象点都是J(Tnβn)上的尖点，所以Aβn(∞)的逆象分支都不是John区域.引理4得证.

定理1的证明 从文献［5］的定理7.22知道，当n为偶数或者n=3，且λ∈R{αn，βn}，或者n ＞3 为奇数且λ∈R{(1，2)，αn，βn}时，Tnλ都是次双曲的.因此也是半双曲的，由引理2知，Tnλ的每个Fatou分支都是John区域.下面讨论当n＞3为奇数且 λ∈(1，2)时的情形.

注意到在这种情形下，Tnλ除了包含2个吸性不变域Aλ(1)和Aλ(∞)外，至多包含另1个周期循环域.由于 Tnλ是实系数的有理函数，故 Tnλ没有cremer点，siegel盘与Herman环.若其仅包含2个吸性不变域，由引理3与引理4的讨论知，它们及其所有的逆像都是John域.

若 Tnλ包含1 个周期循环域{U1，U2，…，Uk}，易见实临界点1-λ必包含在循环{U1，U2，…，Uk}之中.如果{U1，U2，…，Uk}是超吸性循环域或吸性循环域，易证Tnλ是半双曲有理函数.由引理2，Tnλ的每个Fatou分支都是 John区域.如果{U1，U2，…，Uk}是抛物循环域，断定这些抛物周期点及它们的逆像点都不在 ∂Aλ(1)与 ∂Aλ(∞)上.事实上，既然Tnλ的每个Fatou分支都是Jordan区域(见文献［5］定理8.11)，且Tnλ是实系数的有理函数，因此∂Aλ(1)与∂Aλ(∞)与实轴R仅有2个交点.易见此时有斥性不动点q∈(1，+∞)且q∈∂Aλ(1)与q∈∂Aλ(∞)，易证∃q1∈(1-λ/2，1)与q2∈(-∞，0)使得(q1，q)⊂Aλ(1)与(-∞，q2)⊂Aλ(∞)，故q1∈∂Aλ(1)与q2∈∂Aλ(∞).所以∂Aλ(1)与∂Aλ(∞)不包含抛物循环域上的抛物周期点.进一步地，∂Aλ(1)与∂Aλ(∞)也不包含尖点与它们的逆像点.既然Tnλ是实系数的有理函数，易证Tnλ是临界非回归的有理函数.由引理 1，∂Aλ(1)与 ∂Aλ(∞)没有另外的尖点，故Aλ(1)与Aλ(∞)都是John区域.显然，它们的任何逆像Fatou也都是John区域.当这些抛物周期点不是 J(Tnλ)的尖点时，易见Aλ(1)与Aλ(∞)以及它们的任何逆像Fatou都是John区域.当这些抛物周期点是J(Tnλ)的尖点时，由引理3或引理4的讨论知，每1个{Ui(i=1，2，…，k)}及它们的任何逆像Fatou都不是John区域.

结合引理3与引理4，完成了定理1的证明.

［1］ Ruelle D.Thermodynamic formalism:encyclopedia ofmathematics and its applications［M］.Massachusetts:Addison-Wesley Publishing Company，1978.

［2］Yang Chenning，Lee T D.Statistical theory of equations of state and phase transitions.Ⅰ.theory of condensation［J］.Phys Rev，1952，87(3):410-414.

［3］Lee T D，Yang Chenning.Statistical theory of equations of state and phase transitions.Ⅱ.lattice gas and isingmodel［J］.Phys Rev，1952，87(3):415-419.

［4］Qiao Jianyong.Julia sets and complex singularities in diamond-like hierarchical Pottsmodels［J］.Science in China:A，2005，48(3):388-412.

［5］乔建永.重整化变换的复动力学［M］.北京:科学出版社，2010.

［6］ Pommerenke C.Boundary behaviour of conformalmaps［M］.Berlin:Springer，1991.

［7］BeardonA F.Iteration of rational functions［M］.Berlin:Springer，1991.

［8］ McMullen C T.Complex dynamics and renormalization［M］.Princeton:PrincetonUniversity Press，1994.

［9］Milnor J.Dynamics in one complex variable［M］.Princeton:PrincetonUniversity Press，2006.

［10］尹永成.半双曲有理映射的 Julia集［J］.数学年刊，1999，20A(5):559-567.

［11］Qiao Jianyong，Gao Junyang.Jordan domain and Fatou set concerning diamond-like hierarchical Pottsmodels［J］.Nonlinearity，2007，20(1):119-131.