板块元法求目标散射特性中面元划分方法研究*
张文成 周穗华 陈聪聪 张 晨
(青岛雷达声呐修理厂1) 青岛 266100) (海军工程大学兵器工程系2) 武汉 430033)
0 引 言
关于水中物体声散射问题,国内外均有很多学者进行了大量的研究工作[1-3].针对 Rayleigh简正级数的严格理论解只适用于几种简单规则形状物体的情况[4],并且由于Rayleigh简正级数解的形式是一个无穷级数,收敛性差,频率越高需要计算的项越多,在高频情况下导致计算量过大,结果也不准确,学者们发展了许多近似方法,如T矩阵法、时域有限差分法、有限元/边界元法和基于物理声学法的板块元法等.与直接数值积分法相比,由于板块元法具有计算速度快、精度高、算法简洁等特点,在计算目标声散射时得到了广泛应用[5-7].
运用板块元法的关键在于对模型的面元划分,因为面元的划分方法直接决定了算法计算的速度和精度.本文针对板块元法中面元划分问题,首先给出了基于Gordon积分的远场板块元法.然后,借助球体模型,分析了模型面元划分尺度对算法计算速度与精度的影响,并推导出面元划分尺度的确定方法.最后,以圆柱模型为例,通过仿真计算验证了文中所提方法的正确性.
1 基于Gordon积分的远场板块元法
1.1 远场板块元公式
板块元方法是一种对于水下复杂目标回波特性进行计算的有效方法,这种方法在应用物理声学法求解水下目标散射声场时,用一组平面板块元近似目标曲面,把板块元上散射声场的积分运算转化成代数运算,最后将所有板块元的散射声场叠加得到总散射声场的近似值.文献资料表明:板块元法既可以推广到目标近场回波特性研究,也能应用于敷设粘弹性材料的目标散射特性研究[8].与直接数值积分相比,板块元法具有较快的计算速度,计算精度也能够满足要求.
图1所示为收发合置时目标散射示意图和坐标系统,对于远场情况,根据Kirchhoff散射公式,忽略入射声波在每个面元上的不均匀性,目标表面积分域内每个面元的散射声场可以表示为
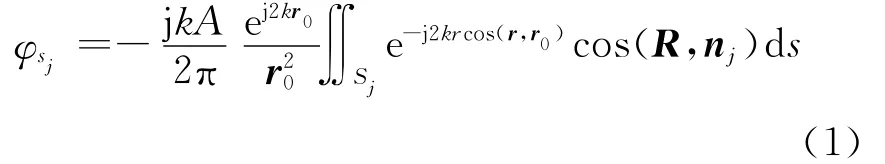
因此,刚性目标远场散射声场和目标强度TS的板块元公式可以表示为

图1 空间目标散射示意图

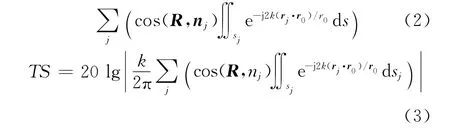
1.2 Gordon积分在板块元求解中的应用
由于Gordon积分可以有效解决常规积分中,当入射波矢量垂直于平面多边形的某个边时,计算结果将出现数值不稳定的问题,而且还能避免大量的坐标变换,可以减少算法工作量[9],因此本文采用Gordon积分算法求解板块元法中积分问题.
对于全局三维坐标(0;X,Y,Z)下的空间多边形平板,如图2所示,Gordon积分算法给出[10]
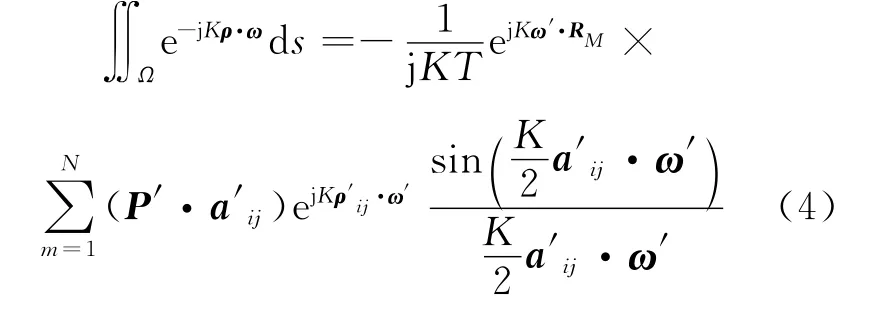
式中:K为常数;ρ为平板上任意一点的位置矢量;ω 为空间三维矢量;在局部坐标系(M;X′,Y′,Z′)中,向量ω′=u′x′+v′y′+t′z′=ω;T 为ω′在平板平面上的投影长度;M为平板上或平板附近源点,RM为源点位置矢量;是ω′在平板所在平面上投影的单位矢量;a′ij描述平板由顶点i到顶点j构成的边的长度和取向矢量,ρ′ij为相应的边中点的位置矢量.时也是有界的,该函数具有稳定解,所以对于在常规积分算法不稳定点处,即垂直入射时,Gordon积分算法依然有稳定值,这就避免了常规积分算法中数值不稳定的问题.假设平板的面积为S,可得到垂直入射时平板目标散射势函数
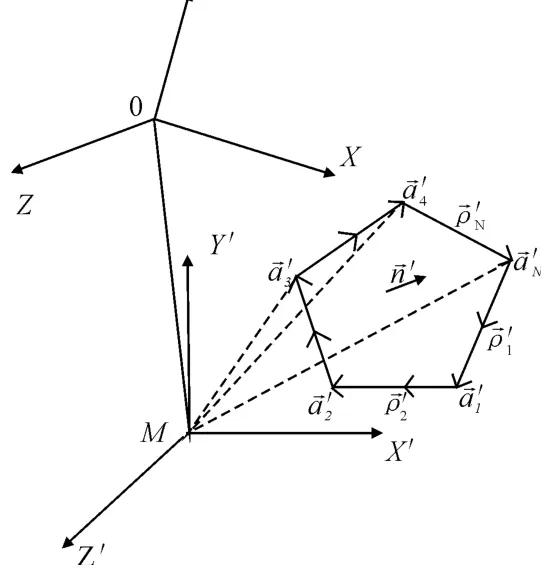
图2 多边形平板与坐标系统

在以上计算积分项过程中,需要将全局坐标系(0;X,Y,Z)转换成局部坐标系(M;X′,Y′,Z′).为了减小工作量,将该坐标变换分为旋转和平移两步进行,就可以避免常规积分算法傅立叶变换积分和Barmett方法中的大量坐标变换,式(4)可以简化成:

2 板块元求解中的面元划分方法
基于Gordon积分的板块元方法求解目标散射场时,面元的划分尺度直接决定了算法的计算速度与精度.文献[9]提到板块元法在面元划分均匀的情况下,为保证计算精度要求L<,即面元尺寸不应大于0.2λ,对于面元划分不均匀的复杂目标,为保证计算精度面元尺寸应更精细.但是如果为高频情况,或者目标曲率半径与波长相比很大时,要求L<将导致计算量过大,因此本文通过研究面元尺度波长比对计算结果的影响,统筹考虑计算精度和计算量,最终确定了面元划分的方法和划分尺寸.
2.1 面元尺寸对算法结果的影响

图3 球体模型
利用ANSYS建立球体模型,设半径r=0.3668m,如图3所示.为了研究板块元法中划分的面元尺寸对算法精度和速度的影响,首先研究目标强度与面元的尺度波长比)之间的关系.分别按照L=50,30,15,10,5mm对球体模型进行了面元划分,不同尺寸划分对应的面元数(element)和结点数(node)见表1.

表1 各面元尺寸对应的面元参数
由表1可见,当按不同的面元尺寸对模型进行划分时,其对应的面元数(或结点数)存在如下平方关系,面元尺寸的减小将导致运算量大幅增加,因此选择合适的面元尺寸是非常有必要的.图4~6分别给出了不同面元尺寸时,由板块元法求得的模型目标强度与尺度波长比的关系,面元为不同尺寸时在=1处计算结果及与解析解的误差见表2,其中r是模型曲率半径.
表2 =1时不同尺寸计算结果
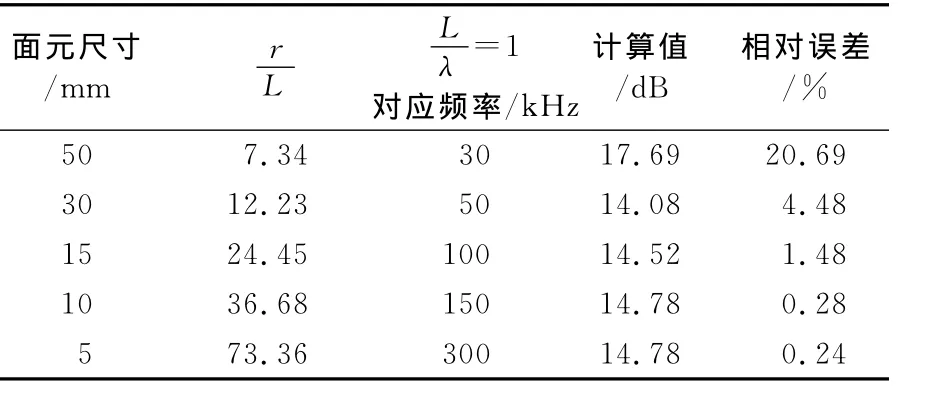
表2 =1时不同尺寸计算结果
面元尺寸/mm rL Lλ=1对应频率/kHz计算值/dB相对误差/%50 7.34 30 17.69 20.69 30 12.23 50 14.08 4.48 15 24.45 100 14.52 1.48 10 36.68 150 14.78 0.28 5 73.36 300 14.78 0.24
分析以上计算结果可以看出,在图4中当L=50mm时需要L≤才能取得很高的计算精度,而当L=30mm时则需要L≤;图5~6中当L=15mm时,只要L≤就能取得较高的计算精度,而对于L=10mm和L=5mm 2种情况,满足L≤λ都能得到足够高的计算精度.表2进一步表明:随着频率的增加,当划分的面元尺寸为一个波长时,由板块元法所得计算结果越来越精确;但是提高到一定程度后,这种随频率变化的趋势就会减弱,如表中L=10mm和L=5mm 2种情况.

图4 L=50,30mm模型目标强度计算结果

图5 L=15,5mm模型目标强度计算结果
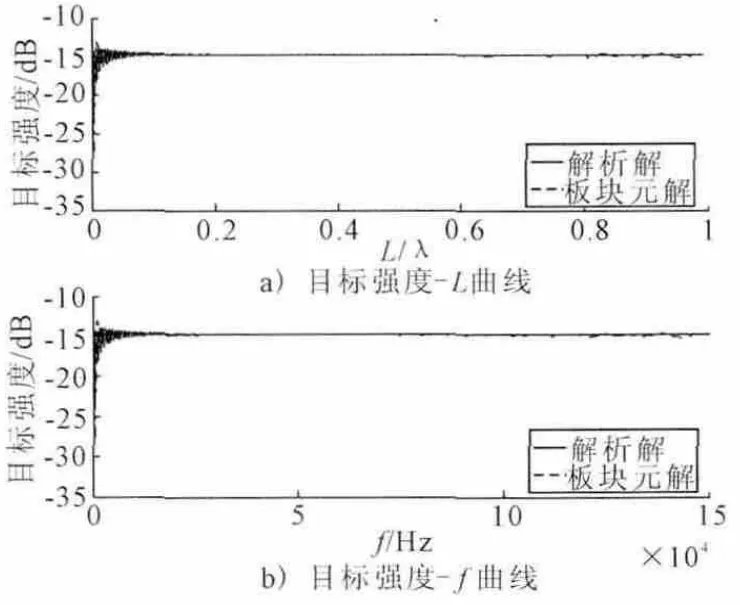
图6 L=10mm模型目标强度计算结果
2.2 面元尺寸的选择标准
通过上文的计算和分析可知,对于曲率半径r=0.366 8m的球体,当≥25时,一个波长内划分一个面元就可以得到较高的计算精度(误差Δ<1.5%).为了验证此结论是否具有一定的普适性,本文又建立了半径r=1m的球体模型,分别以L=33mm≈30)和L=40mm(=25)对模型进行了面元划分,用板块元法的计算结果见图7.
3 验证仿真
为了进一步验证上文提出方法的正确性,下面利用ANSYS建立其他模型进行仿真验证.以圆柱模型为例,假设面元划分最大尺寸L=10mm,根据上文分析确定模型几何参数为r=0.25m,h=1m,共划分面元33 550个,结点16 777个,见图8.
当入射波位于xoy平面并垂直柱轴入射(θ=90°且收发合置)时,计处频率范围是100Hz~150kHz,图8圆柱模型的目标强度与入射频率的关系见图9.图中f=100kHz时目标强度板块元解与解析解的相对误差Δ=0.76%,f=150kHz时相对误差是Δ=1.27%.这一结果说明,当模型曲率半径与面元尺度之间满足≥25时,1个波长内划分1个面元求得的模型板块元解具有足够的计算精度,也说明本文对划分面元尺寸的分析是正确的.
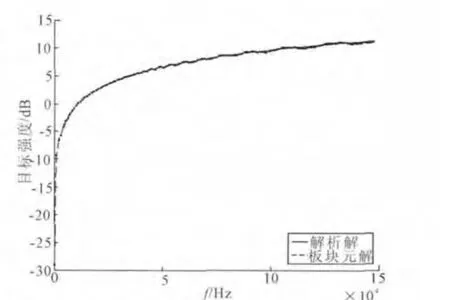
图9 圆柱模型目标强度计算结果
4 结束语
本文研究利用基于Gordon积分的板块元法求解目标声散射特性时面元划分问题,文中给出了基于Gordon积分的远场板块元公式,借助ANSYS建立了球体模型该模型分析了模型面元划分的不同尺度对算法计算速度与精度的影响.然后针对低频和高频的不同情况,推导出模型面元划分尺度的确定方法,并利用不同尺寸的球体模型和圆柱模型进行了仿真验证.本文得出以下结论:用板块元法求解目标散射强度时,对于低频情况,可以增加波长内的面元数(如L≤)以提高计算精度,且不会导致计算量过大;对于高频情况,可以减小波长内所含面元数,以降低运算量,若能保证目标曲率半径与面元最大尺寸之比满足≥25,波长尺度比可以降至1并具有足够高的计算精度.
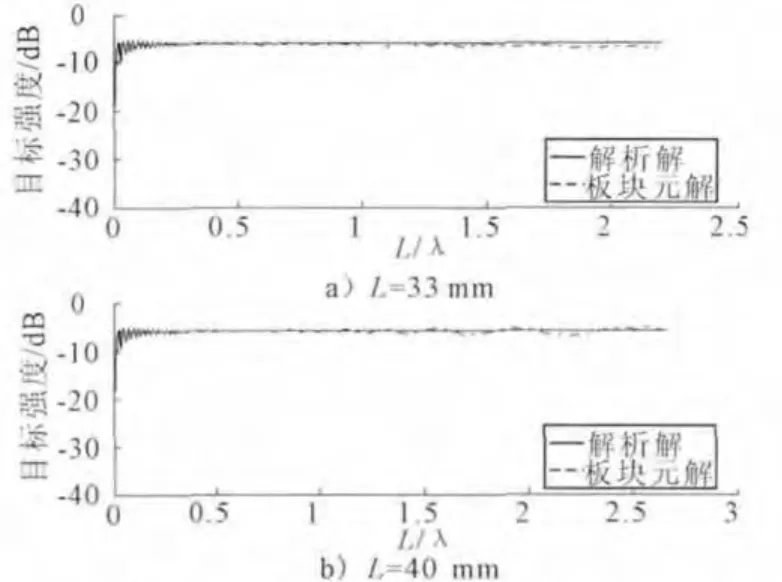
图7 半径r=1m,L=33,40mm目标强度计算结果
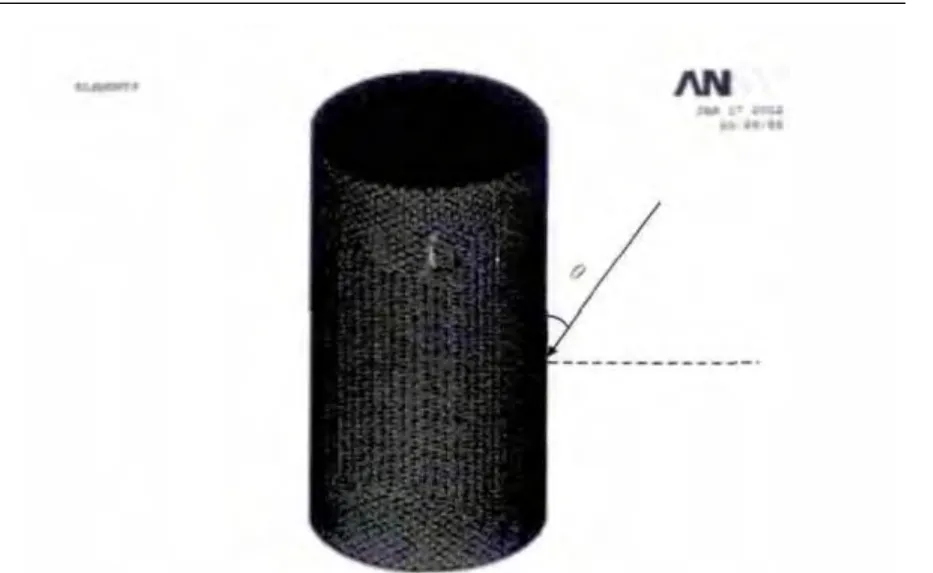
图8 圆柱模型
[1]WATERMAN P C.New formulation of acoustic scattering[J].J.Acoust.Soc.Am,l992,92(1):670-679.
[2]范 军.复杂目标回波特性预报[D].上海:上海交通大学,2002.
[3]FAWCETT J A.Modeling of high-frequency scattering from objects using a hybrid Kirchoff/diffraction approach[J].Journal of the Acoustical Soceity in A-merica,2001,109(4):1313-1319.
[4]冯玉田.水中目标声散射特性研究[D].上海:上海大学,2006.
[5]GORM W,FINN J,JUDITH M B.A numerically accurate and robust expression for bistatic scattering from a plane triangular facet[J].Journal of the A-coustical Soceity in America,2006,119(2):701-704.
[6]考 英,范 军.标准潜艇回波特性计算[J].声学技术,2005,21(2):65-69.
[7]张玉玲.敷设吸声层的水下复杂目标回波特性研究[D].上海:上海交通大学,2009.
[8]张文成,周穗华,蒋安林.聚脲涂层结构模型吸声性能及应用研究[J].武汉理工大学学报:交通科学与工程版,2011,35(3):583-586.
[9]刘成元,张明敏,程广利.一种改进的板块元目标回声计算方法[J].海军工程大学学报,2008,20(1):25-27.
[10] GORDON W B.Far-field approximations to the kirchhoff-helmholtz representations of scattered fields[J].IEEE Trans.Antennas Propagat,1975,23(5):590-592.

