基于车流当量期望冲突量无信号交叉口安全风险分析研究*
袁 黎 刘汉龙
(河海大学土木与交通学院 南京210098)
0 引 言
在探讨交叉口安全性时,大多以冲突点数或事故率的分析方法[1-4],但冲突点数仅探讨车流运行轨迹的冲突,难以反映流量多少对车流冲突的影响;而事故率仅针对已发生的事故数进行分析,无法探讨不同类型冲突的潜在危险性,难以有效的预防事故的发生[5].因此,本文在分析车流冲突特性及不同类型冲突严重性的基础上,考虑车流量大小、车辆位置、冲突概率等因素对交叉口安全的影响,基于期望值的理念,提出了基于当量期望冲突量的路口潜在风险评价方法,旨在为交通工程师设计及改善道路时作参考,并可为用路者对路口的安全性能具有更深一层了解和认识.
1 车流冲突特性分析
交通冲突[6]分为可见冲突和潜在冲突2种,可见冲突为已发生的冲突,而潜在冲突为直觉或想像去感知的冲突,就冲突产生的结果,无论何种冲突均会造成行车的危险,因此本研究探讨的车流冲突包含了可见冲突与潜在冲突两种.
车辆在路段中行驶时,其操作特性可分为跟车、变换车道及超车等行为;然而车辆在通过路口时,则有转向与否两种选择,而当用路者选择转向时,为完成其转向的行为,必须先行将车辆从原来车流中分出,而后并入其转向后行驶方向相同的车流,且转向过程中也可能与其他流向车流发生相互交叉,因此,路口冲突可依车流行为的不同按照冲突角分为3大类:交叉冲突、合流冲突和分流冲突[7].
车流冲突的基本特性为随机性、可避免性、传递性和累加性四大类;随机性为车辆可在任一位置发生交叉、合流与分流的冲突行为,而冲突的任一位置为随机变量,无法预先确认;可避免性为驾驶者出于本身的求生本能,当面临危险时而凭直觉改变自己的驾驶行为来避免发生的冲突;传递性为当车队中某车辆因避免冲突而改变自己的行驶方向或速度时,势必会造成后方或两旁传递的效果,且后方车辆所受的影响不断加深,称之为冲突的传递性和累加性[8-9].
2 车流当量期望冲突量模型的构建
车流冲突可分为可见冲突和潜在冲突2种,且具备可避免性、随机性、累加性等特性,因此难以精确计算车流冲突量,但可基于期望值和排列组合理论,建立车流期望冲突量,由于不同类型车流冲突,对驾驶者造成的潜在危险与肇事严重程度也不同,因此在分析交叉、合流与分流冲突的不同权重基础上,建立车流当量期望冲突量(N′),以期能真实的反映车流冲突行为,即
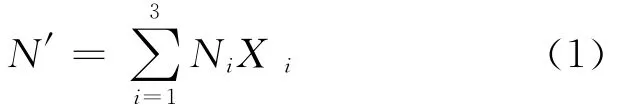
式中:N1,N2,N3分别为交叉、合流、分流期望冲突量;X1,X2,X3分别为交叉、合流及分流的期望冲突权重值.
2.1 车流期望冲突量模型的建立
2.1.1 模型假设
为便于建立车流期望冲突量模型,本研究假设如下:(1)车辆在冲突的位置为一均匀分配的随机变量,因此2股车流中的车辆在任一位置都可能发生冲突,且发生的概率相等,每一冲突位置可同时容许2部以上车辆连续进行交叉,合流或分流;(2)同一时间及空间点仅能存在一辆车,各股合流或分流在并入或分出时无先后次序;(3)以单车道为分析基础,即对于车队而言,冲突只对后方车辆产生影响.
2.1.2 交叉及合流期望冲突量模型
由于车辆交叉和合流行为所产生的冲突特性相似,不同之处仅为所产生的冲突角度不同,因此一起探讨模型的构建.
1)一辆车与N辆车交叉或合流 若假设被交叉或并入的车队由N辆车组成,其可能交叉或合流的位置共有N+1个,即为其所拥有的间距数加上车队最前方和最后方的位置.根据假设1,交叉或合流的位置服从均匀分配且概率相等,则任一位置被交叉或合流的概率为1/(N+1),且当该车辆与第一个位置交叉(合流)时,其冲突量为N,在第二个位置交叉(合流)时,冲突量为N-1,以此类推,则该辆车可能造成的冲突量为0辆车至N辆车,则一辆车与N辆车造成的冲突量和为TC1,该车辆所可能造成的期望冲突量为E(TC1).
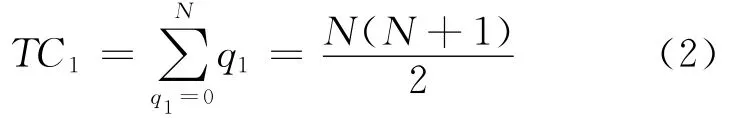

式中:q1为某辆车因交叉(合流)时所造成的冲突量.
2)X辆车与N辆车交叉或合流 当有X辆车与N辆车交叉(合流)时,根据假设3,每一辆车均可能在前车后方交叉(合流),在(N+1)个位置中,任一位置均有可能被0到X辆车交叉(合流).因此,若将X辆车排入到(N+1)个交叉(合流)位置中,在交叉(合流)后,共有(N+X)辆车,依据排列组合,则(N+X)辆车随机排列数为(N+X)!,根据假设3,须除去N 辆车及X 辆车,因后面车辆不可在前车的前方发生交叉或合流的行为,因此X辆车交叉(合流)N辆车中的可能排列数为L,则X辆车交叉(合流)N 辆车的概率为P,即

当2辆车与N辆车交叉(合流)时,其所得的冲突量TC2为
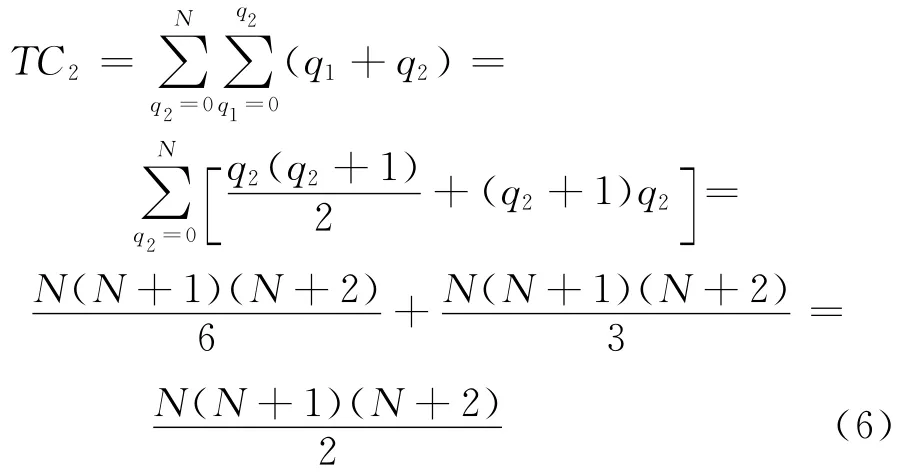
当3辆车与N辆车交叉(合流)时,其所得的冲突量TC3为

若当X辆车与N 辆车交叉(合流)时,则冲突量(TCX)为
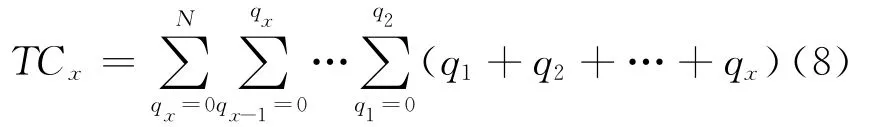
式中:TCx(x=1,2,…,x)为X 辆车所可能产生的冲突量和;qx(x=1,2,…,x)为X 辆车的交叉(合流)冲突量.
由于数列推导过程过于复杂,则可采用归纳的方法,将其简化为数学式,依据式(2),(6)和(7)可得表1.

表1 X辆车与N辆车交叉(合流)冲突量和的归纳
由表1可得,式(8)可表达为
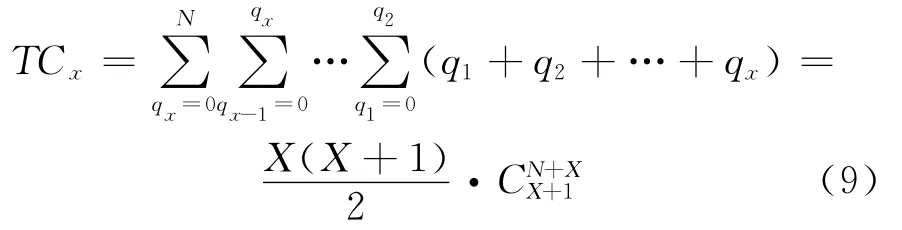
根据假设1,每一种交叉(合流)发生的概率相等,结合式(5)和(9),则该冲突量期望值E(TCx)为
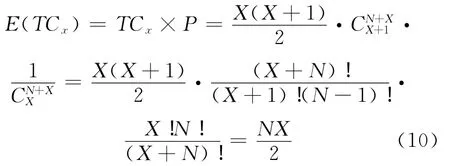
根据式(10),符合期望值E(aX)=aE(X)的定理.
2.1.3 分流期望冲突量模型
1)一辆车从N辆车中分流 根据假设,该车分流所造成的冲突量为其分出位置后方的车辆总数.若被分出车流由N辆车组成,则被分出的位置共有N个,分流的位置服从均匀分配且概率相等,则任一位置被分流的概率为1/N,若第一辆车为分出车辆,则该辆车在第一个位置所造成的冲突量为N-1,而当该辆车在第二个位置分出时,则冲突量为N-2,以此类推,则该辆车可能造成的冲突量为0辆车至N-1辆车,则一辆车与N辆车造成的冲突量和为TC1,该车辆所可能造成的期望冲突量为E(TC1).
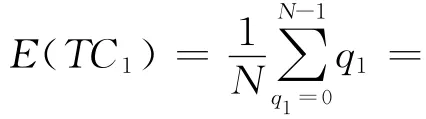
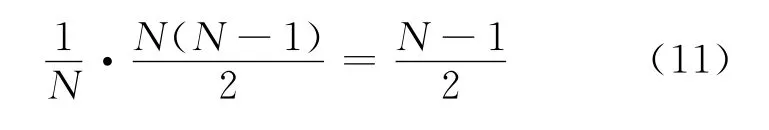
2)X辆从N 辆车中分流 由式(10)可知,由期望值的观点分析冲突量时,符合E(aX)=aE(X)的定理,因此,可推出X辆车从N 辆车分流所造成的期望冲突量E(TCx)为
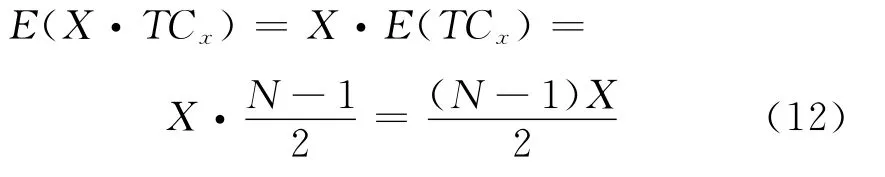
2.1.4 多车道车流期望冲突模型
为简化问题,假设车流量均匀分布在临近路段中每一车道,路口特性仅车道数一项改变,其他条件不变,Nk为第k股车流的车辆数(k=1,2,…,k,且 =N);Xj为第j股车流的车辆数(j=1,2,…,j,且 =X).

图1 交叉冲突型态示意图
以期望交叉冲突模型为例分析,图1a)为单一车道交叉冲突模型,其期望冲突量为E(TCc)=NX.图1b)有2个交叉冲突点,冲突事件彼此独立,因此此型态期望冲突量为E(TCc)=N1X+N2X=(N1+N2)X=NX.同理,图1c)所示的冲突型态期望冲突量为:E(TCc)=N1X+N2X+…+NkX=NX.
由此可得,对任一股X车流,其交叉冲突量模型并未因车道多少而改变;同理可得北向车流分出j股与东向车流每一车道的车流所产生的期望交叉冲突量为:

由以上可知,期望交叉冲突模型与车道数的多少无关.用同样地方法分析多车道期望合流冲突量与分流冲突量,无论合流(分出)车流分支数多少,其冲突量模型相同,因此合流(分出)冲突量并未因合流车流分支数(分出车辆进入邻近路段的车道数)多少而有所不同,因此式(10),(12)同样适用于多车道期望冲突量模型分析,并可计算出交叉口中车流交叉、合流与分流的期望冲突量,进而可得整体路口总期望冲突量.
2.2 车流期望冲突量权重分析
不同类型的交通冲突所导致的交通事故严重程度及事故率是不同的,因而造成的风险程度也有差异,在分析某路口冲突风险性时,应考虑其实际肇事概率的高低与车辆碰撞后的严重程度,亦即,某种类型的冲突肇事概率高且肇事后程度严重时,应立即对该路口进行改善整治;而如果该类型冲突肇事概率高但为轻微刮擦,或者虽肇事程度严重但肇事概率低,则其相应改善策略视具体情况而定[10-11].
本文对车流期望冲突权重模型的分析是依据冲突发生肇事的概率(Pi)与肇事后的严重程度(Bi)两指标而构建的,即
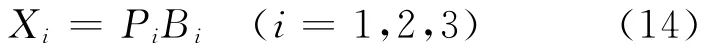
式中:X1,X2,X3分别为交叉、合流及分流的冲突权重值;P1,P2,P3分别为交叉、合流及分流冲突发生事故的概率;B1,B2,B3分别为交叉、合流及分流冲突碰撞后的严重程度.
1)不同类型冲突易肇事的概率 易肇事的概率是指车流的交叉、合流与分流等冲突型态,所发生实际事故的高低.本文通过收集2007年南京地区所辖公路120个无信号交叉路口的事故次数,推算出各类型冲突的易肇事程度的比率关系.由于目前国内事故资料并未按照此3种类型冲突加以分类与记录,本文利用事故资料中肇事车辆的行驶方向及车辆在路口的转向行为,作为归纳交叉、合流与分流肇事的准则.本研究以2小型车事故为主,经统计发生在路口中的事故共计1 173辆,通过准则归类,交叉、合流与分流的事故统计数及其所占比例为,交叉冲突引起的事故数为924起,所占比例为78.77%,合流冲突引起的事故数为150起,所占比例为12.79%,分流冲突引起的事故数为99起,所占比例为8.44%.
2)不同类型冲突肇事后的严重程度 通过对物理碰撞学原理分析,笔者在前期研究中已进行对交叉口不同类型冲突肇事后的严重程度的分析,参见文献[12],可得B1∶B2∶B3=0.099 1∶0.007 8∶0.007 8=12.705 1∶1∶1.
3)权重值计算 为避免扭曲原有期望冲突量的计算,在计算权重一致化时,保持3种类型的冲突权重值的总和为3,见表2.

表2 期望冲突量权重值计算表
根据表2,式(1)可写为
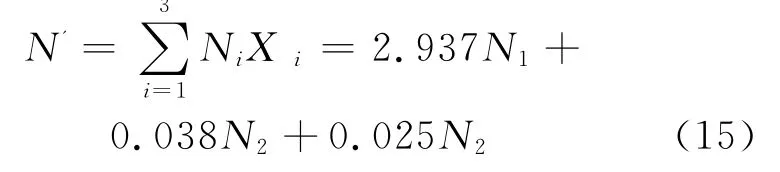
根据式(10)和式(12),可计算出期望交叉冲突量N1、期望合流冲突量N2,期望分流冲突量N3,进而根据公式15,即可计算出交叉口总的车流当量期望冲突量N′.
3 实例应用
本文选取了省道S103桩号K18的一个无信号平面交叉口进行实证研究,见图2,运用上述的车流当量期望冲突量的方法,以此考查此方法的可行性和实用性.
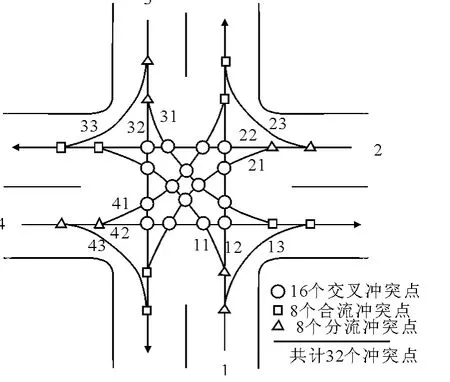
图2 交叉口冲突点及各类型冲突
对该交叉口的流量进行了1h的观测,则平均每分钟每股车队的车辆数见表3.

表3 平均每分钟观测的车流量 pcu/min

表4 南进口期望冲突量计算表 pcu/min
将平均每分钟的车流量代入式(10)或式(12),可求出路口的各类型冲突总的期望冲突量,以南进口左转车的分流冲突为例,其期望冲突量为[5*((5+9+4)-1)/2]=42.5pcu/min,则该路口的期望冲突量计算过程见表4,可得南进口的总交叉期望冲突量为345.5pcu/min,总分流期望冲突量为153pcu/min,总合流期望冲突量为170pcu/min.
同理可得,其他3个进口的交叉、合流与分流期望冲突量,见表5.

表5 各进口总的期望冲突量表 pcu/min
根据式(15),可得该交叉口的车流当量期望冲突量N’为
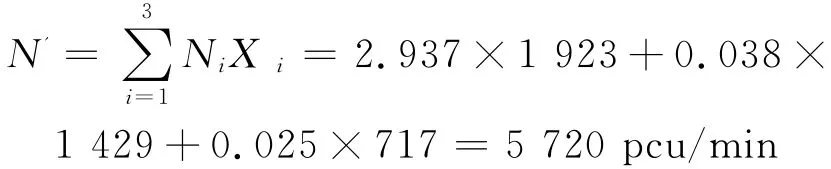
而原来未经权重处理的期望冲突量N为(1 923+1 429+717)=4 069pcu/min,可见若不考虑各类型冲突的权重值时,其期望冲突量将被低估.
根据总的当量期望冲突量的大小,可评估该交叉口的潜在风险性的高低,同样当量期望冲突量模型也可用于不同相位的信号交叉口,更能真实的反映不同相位的信号交叉口车流的交叉、合流与分流等冲突行为,为交叉口的安全分析提供了量化的指标,并为交通工程师设计与评估作参考依据.
4 结束语
1)在分析车流冲突特性的基础上,考虑冲突发生的概率、交通量及车辆位置等因素,建立了交叉冲突、合流冲突及分流冲突期望冲突量的模型.
2)考虑不同类型的交通冲突所导致的交通事故严重程度及易肇事的概率是不同的,本文在分析冲突发生肇事的概率与肇事后的严重程度2个指标的基础上,推算出交叉冲突、合流冲突与分流冲突3种型态的权重值.
3)在期望冲突量模型和各类型冲突权重值的基础上,构建了无信号交叉口车流当量期望冲突模型,旨在能够评估该交叉口潜在风险性的高低,为交通工程师设计与评估作参考依据.
本研究未考虑临界间距及可接受间距对冲突位置的影响,在后续研究中将进一步分析该因素对冲突量的影响,使冲突量模型更加完善;在推算各类型冲突的易肇事概率方面,由于事故收集困难,采用的是南京地区公路事故的资料,在后续研究中将收集更完善的事故资料,使所推算的各冲突的易肇事概率比值更加稳定.
[1]裴玉龙,马 骥.道路交通事故道路条件成因分析及预防对策研究[J].中国公路学报,2003,16(4):77-83.
[2]The Department of Traffic Planning and Engineering.The swedish traffic conflict technique[R].Lund Institute of Technology,Lund University,Broshure,Lund,Sweden,1992.
[3]CHIN Hoongchor,QUEK Sertong.Measurement of traf-fic conflicts[J].Safety Science,1997,26(3):169-185.
[4]潘福全,陆 键.无信号平面交叉口安全服务水平计算模型[J].交通运输工程学报,2007,8(4):104-111.
[5]张 苏.中国交通冲突技术的研究[D].成都:西南交通大学,1997.
[6]袁 黎.公路平面交叉口交通控制安全保障技术的研究[D].南京:东南大学,2007.
[7]袁 黎,项乔君,陆 键.基于交通冲突分析的公路信号交叉口安全评价[J].交通信息与安全,2010,28(1):117-119.
[8]邓蕙菁,王雪松,谢 琨.基于交通冲突技术的交叉口事故多发点判别及致因分析[J].武汉理工大学学报:交通科学与工程版,2012,36(4):370-374.
[9]韩 敏,袁 黎.道路交通次级冲突的研究分析[J].公路工程,2012,37(1):54-58.
[10]刘淼淼,鲁光泉.交叉口交通冲突严重程度量化方法[J].交通运输工程学报,2012,12(3):120-126.
[11]朱 彤,杨晓光.道路交叉口车辆碰撞动态风险估计方法[J].中国公路学报,2012,23(4):96-102.
[12]袁 黎,张 青.基于物理碰撞学理论的车流冲突严重性分析[J].交通运输系统工程与信息,2011,11(1):147-151.

