含皱折船用气瓶安全评价与剩余寿命预测＊

刁爱民 李海涛

（海军工程大学科研部 武汉 430033）

无缝船用气瓶的制造方法主要有3种：冲拨拉伸法、冲压拉伸法和无缝钢管旋压法．在气瓶制造过程中，若采用锻造方式处理瓶口，容易造成气瓶瓶口产生皱折．这些皱折，在船用气瓶充放气产生交变应力的过程中，容易发生扩展，产生疲劳破坏［1－2］．高压气瓶一旦发生疲劳破坏，可能造成泄漏，甚至出现在没有任何征兆如容器泄漏的情况下而直接发生容器破坏，导致突发灾难性事故的发生［3－5］．目前，对于承压设备中的裂纹类缺陷，国内已建立了较完善的安全评定和剩余寿命预测技术［6－8］．但对于船用气瓶中普遍存在的皱折类缺陷，国内外标准规范尚无相关安全评定技术内容，如何对其进行合理化表征，确定其失效模式，科学给出容许的缺陷尺寸和剩余寿命，尚需开展进一步研究．为此，本文针对含皱折缺陷的某型船用气瓶开展安全性评价与剩余寿命预测技术研究，所使用的研究方法，以及相关结论具有的一定的理论意义和工程应用价值．

1 船用气瓶皱折的表征

通过观察高压气瓶收口处的剖面图发现，其收口处的皱折缺陷形貌各异，可归纳为4类，见图1．图1a），b）中的皱折顶部金属基本处于贴合状态；图1c），d）的皱折两侧金属未贴合，留有一定的空隙，其顶部有一定的圆弧半径ρ．为了分析不同皱折类型对气瓶使用安全性的影响，有必要对皱折进行分类和表征，对其进行合理简化，以便于进行区分研究．

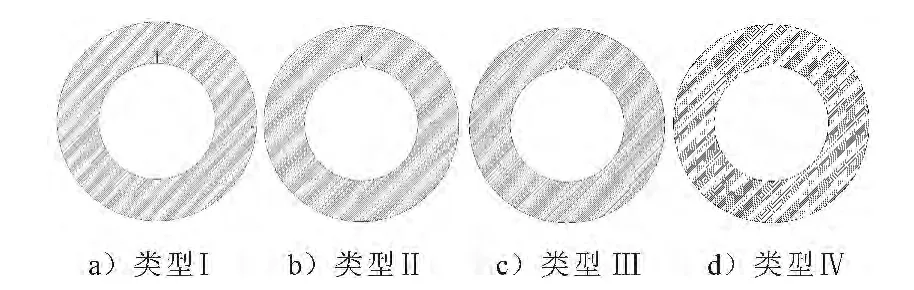
图1 高压气瓶皱折的四种形貌类型

依据不同类型皱折所带来危害等级的不同，可将皱折分为裂纹类和非裂纹类两大类．基于偏保守评价的基础上，对于在宏观目视下皱折底部金属出现贴合或者接近贴合状态时，即ρ≈0，如图1a），b）所示的皱折可近似视为裂纹，按照裂纹进行评价和计算．图1c），d）类型的皱折（ρ＞0），可用皱折的尖锐度和顶部圆弧半径ρ作为皱折表征参数，其中尖锐度定义为皱折的深度a与皱折的半宽b之比即（a／b），见图2．

图2 皱折尖锐度定义示意图

2 皱折处的应力集中系数

2．1 应力集中系数计算方法

在气瓶皱折附近，其应力分布不像裂纹尖端一样具有奇异值，但也存在应力集中现象．对于承受高压且载荷周期性变化的结构而言，应力集中系数较大的结构部位最容易萌生裂纹．在结构强度理论中，某点的应力集中系数λ可定义为结构最大应力与该处薄膜应力之比为

式中：σm为薄膜应力，其计算式为

式中：p为气瓶工作压力；D为气瓶瓶口的中径；B为气瓶瓶口厚度．对于非裂纹类皱折（ρ＞0），应力集中系数可反映皱折对使用安全性的影响程度．本文通过数值方法建立含皱折船用气瓶计算模型，确定皱折处的应力集中系数，研究2个表征参数（a／b，ρ）对皱折处应力集中系数的影响．

2．2 尖锐度a／b对皱折应力集中系数的影响

从某型船用高压气瓶（具体参数略）皱折的分布位置看，基本处于气瓶收口处附近，因此选取计算模型的气瓶外径为D＝300mm，厚度为B＝23mm．先固定皱折顶部圆弧半径为0．5mm，皱折深度a为3mm，通过改变皱折半宽b来分析不同尖锐度a／b对皱折应力集中系数的影响．下面以尖锐度a／b＝6为例分析船用气瓶结构应力分布情况，其计算模型见图3．数值计算模型中弹性模量为207GPa，泊松比为0．3．

图3 含皱折气瓶结构模型图（a／b＝6）

图4 给出了尖锐度a／b＝6条件下气瓶结构的应力云图．可以看出，对于深度3mm、尖锐度为6的皱折最大应力为1 840MPa，该处的尖锐度皱折的应力集中系数为7．79．

图4 含皱折气瓶应力分布图（a／b＝6）

分别计算皱折顶部圆弧半径ρ为0．3，0．5，0．7mm时，不同尖锐度皱折处的应力集中系数，结果见图5．由图可知，随着皱折尖锐度的增加，其皱折处的应力集中系数也随之增大，但当尖锐度超过1时，应力集中系数增大的速度降低，曲线变得平缓．

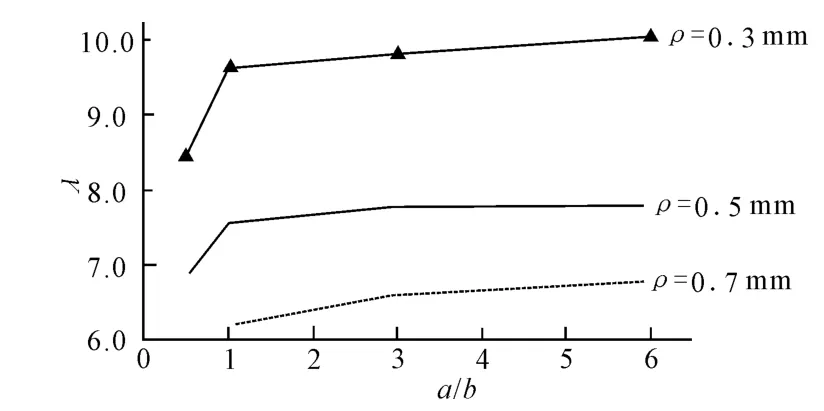
图5 应力集中系数λ与尖锐度a／b的关系

2．3 顶部圆弧半径ρ对皱折应力集中系数的影响

为了研究皱折尖锐度一定时顶部圆弧半径ρ对应力集中系数的影响，选取计算工况为：皱折深度a为3mm、尖锐度为3（a＝3mm，b＝1mm），顶部圆弧半径ρ分别为0．8，0．6，0．4，0．2mm．图6给出了圆弧半径ρ为0．8mm时气瓶结构的应力分布图．图7给出了尖锐度分别为1，3，5条件下应力集中系数与圆弧半径之间的关系曲线．

图6 含皱折气瓶应力分布图（ρ＝0．8mm）

由图7可见，皱折应力集中系数随着圆弧半径的增大而减小，且圆弧半径越大，应力集中系数的变化趋缓．随着尖锐度a／b的增大，应力集中系数略有上升，但变化不大．从对应力集中系数的影响程度来看，皱折表征参数顶部圆弧半径ρ对应力集中系数的影响更加显著．

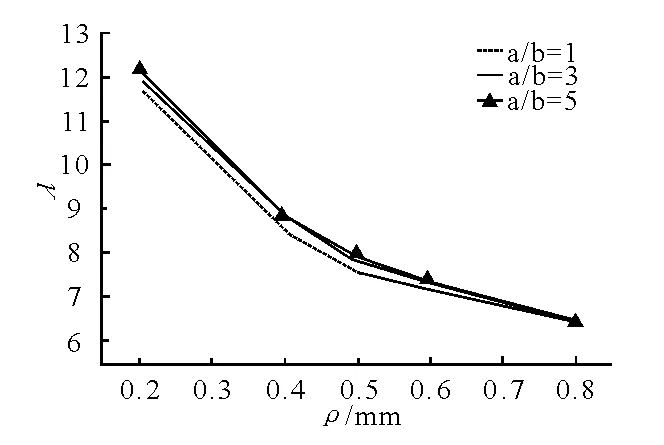
图7 应力集中系数λ与ρ的关系

3 含皱折船用气瓶安全评价及剩余寿命预测

3．1 皱折的处理

对皱折应力集中系数的研究结果表明，当尖锐度a／b大于1（对应皱折的顶部夹角小于90°）时，尖锐度a／b的变化对于应力集中系数影响不明显．随着顶角圆弧半径ρ增大，应力集中系数λ衰减非常明显，在圆弧半径ρ达到0．8mm时，其衰减过程趋缓．为此，基于偏保守原则，当皱折顶部圆弧半径ρ≤1mm，将其按裂纹处理；当皱折顶部圆弧半径ρ＞1mm，将其按非裂纹类缺陷进行处理．

3．2 非裂纹类皱折的疲劳裂纹萌生寿命

根据以上分析，当皱折的顶角圆弧半径ρ＞1 mm时，将其归为非裂纹类缺陷处理．取顶角圆弧半径为0．8mm的皱折进行偏保守分析，取皱折深度为3mm，尖锐度为1．数值计算时采用双线性本构材料模型，其中弹性模量为207GPa，切线模量为2．957GPa．图8给出了该计算工况下气瓶的应变分布图，其结构最大应变值为1．09%，最大应变幅值为0．545%．

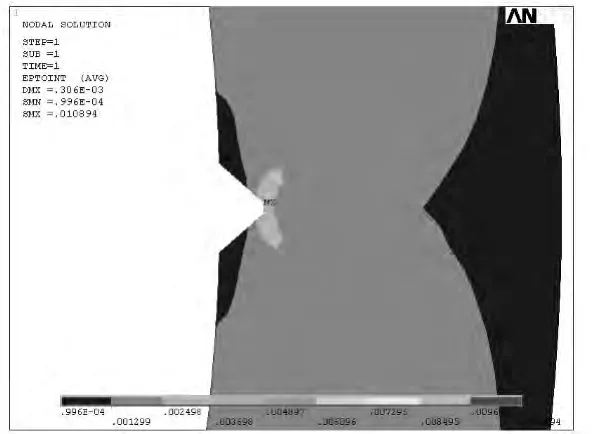
图8 含非裂纹类皱折气瓶应变图（a＝3mm）

通过气瓶材料轴向疲劳试验得到的疲劳性能曲线即应变幅值与循环次数的关系见图9．经计算，3mm深皱折计算得出的0．545%应变幅值所对应的疲劳循环次数为191 529次．考虑到疲劳分析20倍安全系数，可知其疲劳裂纹萌生寿命不低于9 576次．

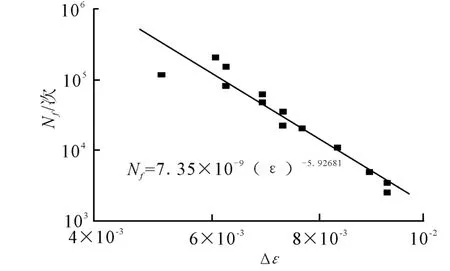
图9 应变幅－疲劳寿命关系曲线

3．3 裂纹类皱折的安全评价

选取3种皱折，深度分别取为3，4和5mm，皱折长度均为55mm．这3种皱折缺陷可表征为a＝3，4和5mm，2c＝55mm的半椭圆形表面裂纹．

通过疲劳裂纹扩展速率试验得到船用气瓶在工作环境下的疲劳裂纹扩展速率：

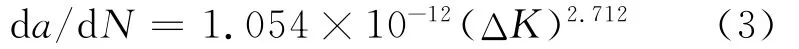
式中：ΔK为应力强度因子．对此3种皱折进行疲劳裂纹扩展计算，计算疲劳循环20 000次后的最终扩展尺寸．表1给出了深度为4mm皱折疲劳扩展结果．

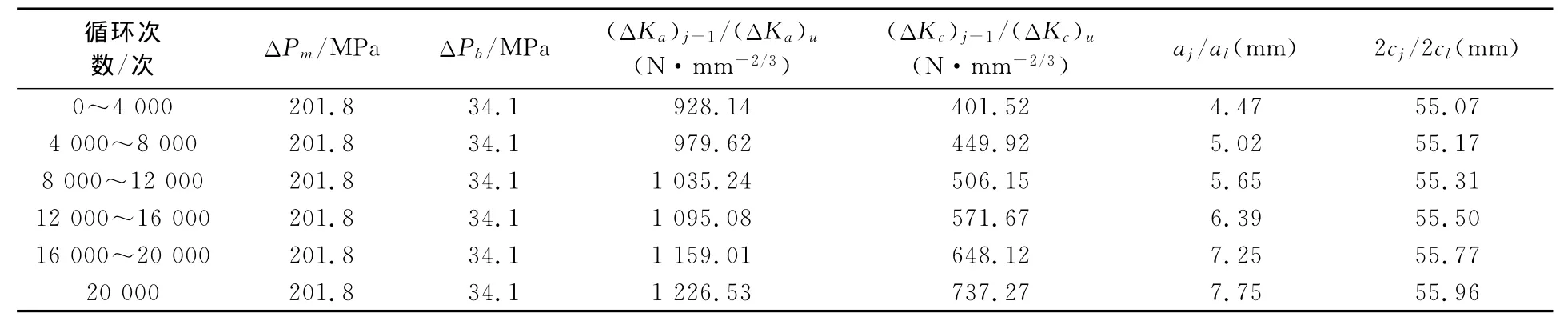
表1 深度4mm皱折疲劳扩展计算结果

对3种皱折的最终评定结果在通用失效评定图上进行安全评定［9］，这3种皱折的评定点仍位于安全区内，即含有此3种皱折的气瓶可保证安全使用．对不同深度皱折进行疲劳分析计算，确定疲劳循环20 000次仍能保证安全的皱折深度．不同皱折深度疲劳循环20 000次后的评定结果见图10．由图可知，当皱折深度a＝11．0mm时，评定点位于安全区内，当皱折深度a＝11．1mm时，评定点落在评定线上，因此，可认为皱折临界深度为11．0mm．

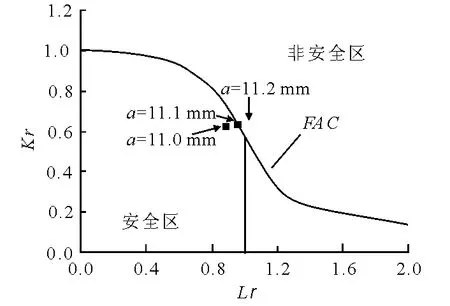
图10 皱折疲劳评定临界深度计算

3．4 试验验证

为了分析以上数值分析结果的正确性，本文开展了含人工预制皱折缺陷气瓶的疲劳试验研究工作，预制的皱折情况见表2．

表2 试验用气瓶人工预制皱折尺寸参数 mm

试验加载疲劳循环载荷20 000次后，这些皱折未发现扩展，声发射检测无明显缺陷活动信号．试验结果表明，对于5mm的皱折，在疲劳循环20 000次后是安全的．

4 结 论

1）对于含皱折缺陷的船用气瓶，当其皱折顶部圆弧半径ρ≤1mm，可按裂纹进行处理；当皱折顶部圆弧半径ρ＞1mm，可按非裂纹类缺陷进行处理．

2）在其他参数一定的情况下，非裂纹内皱折的应力集中系数随着皱折尖锐度的增加而增大，随着圆弧半径的增大而减小；相比较而言，顶部圆弧半径的变化对应力集中系数的影响更加显著．

3）对于该型船用高压气瓶而言，当皱折深度≤5mm时，在经过20 000次循环使用后能仍保证其使用安全．

［1］孙训方，方孝淑．材料力学II［M］．北京：高等教育出版社，2009．

［2］张凤武．高强钢疲劳裂纹扩展研究［D］．武汉：武汉理工大学，2011．

［3］范志超，陈学东，蒋家羚．16MnR压力容器用钢断裂韧性的概率模型［J］．固体力学学报，2006，27（1）：65－68．

［4］段 权，程光旭，姜培正．16MnR压力容器用断裂韧性的概念模型［J］．西南交通大学学报，2000，34（4）：71－74．

［5］段 权．16MnR压力容器用钢疲劳裂纹萌生寿命及其分布研究［C］／压力容器先进技术，第七届全国压力容器学术会议论文集，北京：2009：140－143．

［6］ANDERSON T L．Fracture mechanics fundamentals and applications［M］．USA：Taylor ＆Francis Group，2011．

［7］PARIS P C，ENDOGEN F A．Critical analysis of crack propagation loan［J］．Journal of Basic Engineering，1963，85（4）：528－534．

［8］ZHANG Liang，LIU Xuesong．Fatigue cracking initiation for Al－Zn－Mg alloy welded joint［J］．ACTA Metallurgical Sinica，2012，25（3）：235－240．

［9］陈 钢，钟群鹏，余寿文，等．GB／T 19624—2004在用含缺陷压力容器安全评定［S］．北京：中国标准出版社，2005．