一种多维尺度分析到达时间差定位算法
王 琳,蒋武扬,徐昌庆
(上海交通大学 上海市北斗导航与位置服务重点实验室,上海 200240)
1 引言
定位技术已经广泛应用于各个领域,例如通信、矿业、公路、铁路等等[1-5]。在无线信号广泛覆盖的今天,无线定位技术得到了越来越多的重视[6]。在众多无线定位系统中,到达时间差定位(time difference of arrival,TDOA)是一种被广泛应用的定位方法。它的原理是通过测量目标点与多个已知参考点之间无线信号传输的时间差,得到多组双曲线方程并求出位置信息。与到达时间定位(time of-arrival,TOA)相比,TDOA技术不需要所有节点的时间同步,也不需要信号带有时间戳,实现较为简便。经过学者们的多年研究,TDOA算法得到了不断的更新和完善。文献[7]提出的早期算法是一种简单方便的算法,但其在参考点较多时无法使用。较为经典的泰勒(Taylor)级数展开法精度高、稳定性好,但是需要估计初始位置和递归求解,计算量较大[8]。文献[9]提出的算法即二步加权最小二乘法是另一种经典算法,该算法不需要估计初值并且计算量较小,但是在噪声较大时性能会明显变差。
近年来,一种新型的基于多维尺度分析(multi-dimensional scaling,MDS)的TDOA定位算法(以下简称MDS算法)[10]引起了研究人员的关注。该方法基于多维尺度分析将TDOA定位问题建模为矩阵范数的最优化问题,然后通过子空间分析将最优化问题转化为线性方程的求解。该算法定位精度高,计算量较小,并且在噪声较大时表现良好。
本文指出MDS方法[10]的一处疏漏,即不能通过标量积矩阵的正定性将最优化问题转化为线性方程求解问题。本文通过分析位置坐标矩阵的列向量的线性相关性,借助几何意义,得出无论列向量是否线性相关,都有目标线性方程成立,从而严格地证明了原算法的正确性,使得原算法的理论基础更加坚实。
2 系统模型与MDS算法概述
2.1 系统模型
本文针对参考点和目标点位于二维平面上的情形进行讨论。
假设有M个位置已知的参考点分布在一个二维平面上,且要求它们并不在一条直线上。设参考点的坐标为(xm,ym)T,m=1,2,...,M。设目标点的坐标为(x0,y0)T,这里假定目标点不与任何一个参考点的位置重合。则第m个参考点到目标点的距离为:
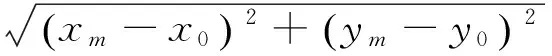
(1)
第m个参考点到目标点的距离与第1个参考点到目标点的距离之差为:
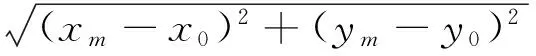
(2)
为方便计,补充定义d1,1=0,d0,1=-d1。
另一方面,dm,1可以通过到达时间差TDOA来测得。设测量所得的目标点发送信号到达第m个参考点的时间与到达第1个参考点的时间的到达时间差(即TDOA)为:τm,1,m=2,3,...,M,则有:
dm,1=cτm,1,m=2,...,M
(3)
其中c表示信号的传播速度。由式(2)及式(3)可得:
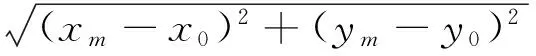
(4)
式(4)是一组非线性方程,其中c是已知量,(xm,ym)T,m=1,2,...,M是已知量,τm,1,m=2,3...M是测量值,(x0,y0)T是待求量,是求解的目标。
2.2 MDS算法概述
MDS算法基于多维尺度分析将TDOA定位问题转化为矩阵范数的最优化问题,然后通过子空间分析将最优化问题转化为线性方程的求解问题[10]。以下概述MDS算法的要点。
设wm=(xm,ym,idm,1)T,m=1,2,...,M,设w0=(x0,y0,id0,1)T,其中i是虚数单位。定义位置坐标矩阵为:
(5)
则Z∈M×3是一个包含目标点位置信息x0,y0,d0,1的矩阵。定义标量积矩阵为:
B=ZZT
(6)
则B∈M×M。通过计算可知B的第m行第n列的元素为:

(7)
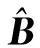
(8)
其中‖·‖F表示矩阵的Frobenius范数。
以下将式(8)的矩阵范数最优化问题转化为线性方程求解问题。由于B是实对称矩阵,故可正交相似于对角矩阵。又由于Z为M×3矩阵,而B=ZZT,则r(B)≤r(Z)≤3,其中r(·)表示矩阵的秩。因此B至少有M-3个零特征值,记零特征值对应的特征向量所组成的矩阵为Un,则:
BUn=0
(9)
由式(6)可将式(9)转化为:
ZZTUn=0
(10)
如果矩阵Z的列向量线性无关,则有:
ZTUn=O
(11)
由于Un是实矩阵,而Z仅有第三列元素是纯虚数,其它元素皆为实数,故可将Z的第三列元素的虚数符号i全部去掉,式(11)仍然成立。记为

(12)
则可解得:
(13)
式(13)中,v0中的分量x0,y0即是所求的目标点坐标。
3 基于位置坐标矩阵列向量线性相关性的MDS算法
3.1 基于标量积矩阵正定性的MDS算法
文献[10]中的MDS算法是基于标量积矩阵B的正定性。具体地说,文献[10]依据标量积矩阵B的正定性来证明式(11)。证明过程如下:


3.2 基于位置坐标矩阵列向量线性相关性的MDS算法
本文给出一种基于位置坐标矩阵列向量线性相关性的MDS算法。该算法总体思路是:当位置坐标矩阵Z的列向量线性无关时,式(11)成立;而当位置坐标矩阵Z的列向量线性相关时,式(11)仍然成立。从而,通过对位置坐标矩阵Z的列向量线性相关性的分析,严格地证明了MDS算法的正确性,使得MDS算法的理论基础更加坚实。
当位置坐标矩阵Z的列向量线性无关时,2.1节已经推导出式(11)成立。
当位置坐标矩阵Z的列向量线性相关时,式(11)成立的理由如下。
如果矩阵Z的列向量线性相关。因为Z是M×3矩阵,那么Z的列秩≤2,因此Z的秩r(Z)≤2,这就等价于Z的行秩≤2,即Z的任意三个行向量都线性相关。由式(5)可见,Z的第三列为纯虚数,其它列为实数,为简便计,可以考虑去掉第三列的虚数符号i,这样做并不影响行向量的相关性,于是可设:
(14)
注意到:
dm,1-d0,1=(dm-d1)-(-d1)=dm,
m=1,2,...,M
(15)
因此:
(16)


(17)
(xn-x0,yn-y0,dn)=
a1(xk-x0,yk-y0,dk)+
a2(xm-x0,ym-y0,dm)
(18)
考虑式(18)的几何意义。由于(xk,yk)表示a1,a2中第k个参考点的位置,(x0,y0)为目标点位置,那么容易看出,(xk-x0,yk-y0)中以目标点为起点、以第k个参考点为终点的向量,而dk表示该向量的长度。于是,式(18)可以写成:
(19)
下面根据a1,a2的正负分类讨论:
分类1:假如a1,a2有且仅有一个等于0,不妨设a1=0,a2≠0,则式(19)的第一个方程可以写为:
(xn-x0,yn-y0)=a2(xm-x0,ym-y0)
(20)
这表示向量(xn-x0,yn-y0)与(xm-x0,ym-y0)共线。同时,由式(19)的第二个方程可知:
dn=a2dm
(21)
由于dn,dm>0,故a2>0。因此(xn-x0,yn-y0)与(xm-x0,ym-y0)共线且同向。
分类2:假设a1,a2均不为0,不妨设a1≤a2,则可以分为以下几类:
分类2.1:0 (22) 根据向量范数的三角不等式,可知: ‖a1(xk-x0,yk-y0)+a2(xm-x0,ym-y0)‖ (23) 当且仅当向量a1(xk-x0,yk-y0)与a2(xm-x0,ym-y0)共线并且同向时等号成立。又由于0 分类2.2:a1<0 (24) 然后,与分类2.1的原理相同,可知式(24)成立的充要条件是:向量(xn-x0,yn-y0),-a1(xk-x0,yk-y0),a2(xm-x0,ym-y0)共线且同向。由于a1≤a2<0,因此可得向量(xn-x0,yn-y0),(xk-x0,yk-y0),(xm-x0,ym-y0)共线且同向。这与分类2.1得出的结论相同。 分类2.3:a1≤a2<0。由于dl≥0恒成立,因此式(19)的第二个方程无法满足,因此这种情况下无解。 至此,根据a1,a2的正负分类讨论结束。 根据以上的讨论,可以得出结论1: 结论1:如果矩阵Z的列向量线性相关,则(xn-x0,yn-y0),(xk-x0,yk-y0),(xm-x0,ym-y0)这三个向量中至少有两个向量共线且同向。 总结和分析上述结论,可得到结论2: 结论2:如果Z的列向量线性相关,则在M个参考点中任取3个点,目标点都一定落在其中至少两个参考点所连成的直线上,并且目标点位于该直线上参考点的同侧。 假设所有参考点不在一条直线上,因此满足以上要求的情况只能是: 结论3:如果Z的列向量线性相关,则所有参考点沿着两条相交的直线排列,而目标点位于这两条直线交点上;同时,在每条直线上,目标点都位于该直线上所有参考点的同侧。 假设参考点和目标点在几何上满足结论3所述的排布,则易知矩阵Z的列线性相关。在这种情况下,不妨设第k,m,n个参考点不在结论3所述两条直线的同一条直线上,那么向量(xn-x0,yn-y0),(xk-x0,yk-y0),(xm-x0,ym-y0)并不两两线性相关,因此可知矩阵Z的前两列的列秩为2。而由于Z的所有三列的列向量线性相关,那么必有Z的第三列可由前两列线性表示,因此: dm=k1(xm-x0)+k2(ym-y0),m=1,2,...,M (25) 其中,实数k1,k2不同时为0。由式(16)(25)可得: (26) 由式(5)(16)可知: (27) 则式(10)等价于: (28) (29) 其中am∈R是常数。又由式(28)可知: (30) 因此,根据式(29)及式(30)可以得到: (31) 从而: 要使式(32)成立,存在两种可能的条件: 条件2:k1+k2-1=0。即: k1+k2=1 (33) 为简便计,不妨假设第1个参考点和第2个参考点与目标点不共线,即向量(x1-x0,y1-y0)与向量(x2-x0,y2-y0)线性无关。根据式(29),有: (34) 利用式(1),则式(33)(34)可以表示为: (35) 其中,xm0=xm-x0,ym0=ym-y0,m=1,2。可设: (36) 将式(35)转化为: (37) 进一步,可设: k1=cosθ,k2=sinθ (38) 那么,式(37)可以转化为: (39) 也就是: (40) 这表明θ=α=β。根据α,β的定义式(36),可以得到: (41) 这样,就得到(x1-x0,y1-y0)与向量(x2-x0,y2-y0)线性相关,与假设矛盾。那么条件2无法成立。 由上述对条件1和条件2的分类讨论可知,要使式(32)成立,必须有式(11)成立。 总结全文分析如下:如果矩阵Z的列向量线性无关,则式(11)成立;如果矩阵Z的列向量线性相关,则参考点和目标点在几何上必须满足结论3所述的排布,此时必须有式(32)成立,进而式(11)成立。由此可见,无论矩阵Z的列向量是否线性相关,式(11)始终成立。这样就完成了对文献[10]疏漏之处的严格证明。总之,基于位置坐标矩阵列向量线性相关性的MDS算法克服了基于标量积矩阵正定性的MDS算法[10]的缺陷,在理论上更加严格。 本文在概述一种基于MDS的TDOA定位算法基础上,指出基于标量积矩阵正定性的MDS算法在推导中存在的一处疏漏,即不能通过标量积矩阵B的正定性来得出目标线性方程式(11)。接着,本文提出一种基于位置坐标矩阵列向量线性相关性的MDS算法,该算法从位置坐标矩阵Z的 列向量的线性相关性出发,当Z的列向量线性无关时,式(11)成立;而当Z的列向量线性相关时,通过分析Z的列秩和行秩,得出参考点和目标点所必须满足的几何排布条件,并验证在该条件下仍有式(11)成立,从而严格地证明了MDS算法的正确性,使得MDS算法的理论基础更加坚实。 本文仅针对参考点和目标点位于二维平面上的情形进行讨论。对于参考点和目标点位于三维空间中的情形,还有待进一步的研究。 致谢:本项研究工作得到了中国卫星导航系统管理办公室(北斗办)和上海市科学技术委员会的联合资助,资助课题编号为BDZX005. [1] ZEKAVAT R,BUEHRER R M.Handbook of Position Location:Theory,Practice and Advances[M].Hoboken N J:Wiley-IEEE Press,2011. [2] 胡可刚,王树勋,刘立宏.移动通信中的无线定位技术[J].吉林大学学报:信息科学版,2005,23(4):378-384. [3] 王雪莉,卢才武,顾清华,等.无线定位技术及其在地下矿山中的应用[J].金属矿山,2009(4):121-125. [4] 胡明伟.无线定位技术应用于实时交通信息采集研究[J].深圳大学学报:理工版,2007,24(3):246-251. [5] 王思诗.高速列车用户无线网络定位技术研究[D].北京:北京交通大学,2012. [6] 毕晓伟.无线定位技术研究[D].重庆:重庆大学,2011. [7] FANG B T.Simple Solutions for Hyperbolic and Related Position Fixes[J].IIEEE Transactions on Aerospace and Electronic Systems,1990,26(5):748-753. [8] FOY W H.Position-location Solutions by Taylor-series Estimation [J].IEEE Transactions on Aerospace and Electronic Systems,1976(2):187-194. [9] CHAN Y T,HO K C.A Simple and Efficient Estimator for Hyperbolic Location[J].IEEE Transactions on Signal Processing,1994,42(8):1905-1915. [10] WEI He-wen,PENG Rong,WAN Qun,et al. Multidimensional Scaling Analysis for Passive Moving Target Localization With TDOA and FDOA Measurements[J].IEEE Transactions on Signal Processing,2010,58(3):1677-1688.
≤‖a1(xk-x0,yk-y0)‖+‖a2(xm-x0,ym-y0)‖
=|a1|‖(xk-x0,yk-y0)‖+|a2|‖(xm-x0,ym-y0)‖
=a1‖(xk-x0,yk-y0)‖+a2‖(xm-x0,ym-y0)‖
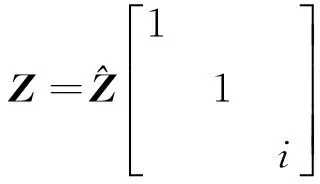


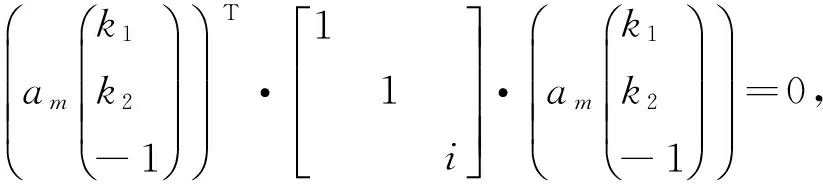
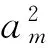
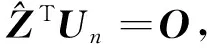

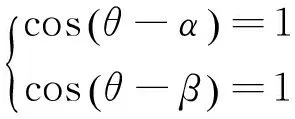
4 结束语

