一种基于感知概率的室内定位匹配算法

杨 萌，修春娣，邹 坤，杨东凯，刘 源

(1.北京航空航天大学 电子信息工程学院，北京 100191；2.中国电信集团 上海市电信公司，上海 200120)

1 引言

基于位置的服务被应用于很多领域，大部分的设备是基于室外定位系统，如全球定位系统(global positioning system，GPS)。但是基于GPS的定位需要视距来保证可靠的定位精度，并不适用信号多变且环境复杂的室内定位系统，因此基于无线局域网络中无线保真(wireless fidelity，WiFi)的室内定位技术得到了广泛的应用。现今很多建筑中装有WiFi接入点，现有的基础设施可以基本上满足定位需求，因此可以减少经济开支和额外的硬件装配。

基于WiFi的室内定位方法主要有基于传播模型的定位方法和基于指纹匹配的定位方法。基于传播模型的定位方法不需要预先采集接入点(access point，AP)的信号强度，只需找出射频信号在室内环境中的传播模型，依据信号传播模型和设备与AP之间的信号强度差来估计位置信息，可以实现距离的粗略估计，不能提供准确的定位，因为接收信号强度(received signal strength，RSS)[1]很容易受周围环境影响。指纹匹配的定位算法构建信号强度与定位位置之间的映射关系，使用存储所有参考点(reference point，RP)的RSS信息的数据库来进行匹配计算，可以获得较好的定位效果，因此，本文的工作主要是基于指纹定位技术。

基于指纹匹配的室内定位技术通常工作在两个阶段：离线训练阶段和在线阶段。在离线训练阶段，目标区域中所有RP接收到的来自可用AP的信号强度信息形成指纹数据库。在线定位阶段，将实时采集的RSS与指纹数据库中的指纹进行匹配，从而得到定位设备的位置信息。

基于指纹匹配的定位算法分为确定型和概率型两种算法。确定型定位算法主要是比较指纹库中的指纹与定位阶段采集的RSS之间的相似度，选择最大相似度的指纹对应的位置作为测量设备的估计位置。常采用的匹配算法为k近邻(k-nearest neighbor，k-NN)[2-6]，该算法首先采用欧式距离度量指纹库中指纹与实测RSS之间相似度，找出相似度最大k个位置，然后计算这k个位置的质心得到估计位置。概率型算法把实测RSS与指纹库中指纹的匹配过程看成概率估计问题，基于RSS信号的统计特性，建立室内环境中射频信号的概率分布模型，解决了复杂环境下RSS值的不确定性。常用的基于概率型算法为最大似然算法(maximum likelihood，ML)[2]，基于贝叶斯框架理论，将后验概率转化为似然概率问题，匹配最大的似然概率，得到估计位置信息。常用来计算似然概率的方法有理想高斯模型[7]，直方图统计模型[8]和核密度估计方法[9]。其中核密度估计方法不利用有关数据分布的先验知识，对数据分布不附加任何假定，是一种从数据样本本身出发研究数据分布特征的方法，可以更准确的表征复杂信号的分布，从而提高定位精度。

在离线训练阶段，并非每个RP都能接收到测试区域内的所有AP信号，RP点可以感知到相应的AP信号样本越多，可用于匹配计算的信息越多，该RP点指纹的可靠性越高，因此本文中引入感知概率的定义，来表征定位区域内不同位置的信号分布特征，并将感知概率结合k-NN算法，提出修正k-NN，与常用理想化高斯分布模型不同，本文采用核直方图统计模型和密度估计方法计算似然函数，并将感知概率和核密度估计结合ML算法，提出修正ML算法。

2 修正算法

2.1 感知概率

由于信号衰减和障碍物的影响，同一个采样设备很难在不同的位置甚至在同一位置获得相同的信号强度。但是由于环境和AP功率的稳定性，同一个采样设备在相同的位置获得特定AP信号的概率是相对稳定的。如果在测试位置处的AP信号强度小于采样设备可以感知到的最小信号强度，表示设备不能够感知到AP信号，用一个固定的信号强度代替不能感知到的信号强度信息。因此，感知概率定义为感知到的AP次数与总的训练样本数之比[2]。

假设在一个室内测试区域中有n个RP和m个AP，在离线训练阶段，AP信号采集可以看成一个伯努利过程。对特定RP，每次采样可以获得一个二进制序列B=(b1,b2,…bj,…,bn)，其中bj∈(0,1)。对于第i个RP，可以感知到的第j个AP的次数为nbj|ω(1|ωi)，总的训练样本数为N(1|ωi)，因此第i个RP对第j个AP的感知概率可以定义为：

(1)

由感知概率的定义可知，感知概率可以一定程度上表征测试区域内不同位置的信号分布情况，因此基于感知概率的修正算法可以提高定位算法精度。

2.2 修正k-NN算法

在离线训练阶段，采集的样本存储为指纹数据库，在线定位阶段，将采集到的信号强度信息与指纹数据库中的指纹信息进行匹配，对每一个RP点，相应的欧氏距离定义为：

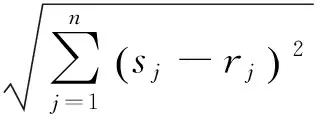
(2)

式(2)中，S=(s1,s2,…,sn)为实测信号向量，Ri=(r1,r2,…,rn)为指纹库中存储的第i个RP的指纹信息。

修正算法将感知概率和欧氏距离结合起来，定义了感知欧氏距离。假设离线训练阶段感知概率相对稳定，记为Pbj|ω(1|ωi)，那么在线阶段可以感知到信号的概率是Pbj|ω(1|ωi)，计算欧氏距离时利用离线阶段的RP位置指纹进行计算；同样地，不能感知到信号的概率是1-Pbj|ω(1|ωi)，此时采样特定数值C进行匹配计算。两者之和即为感知欧氏距离。如公式(3)所示：

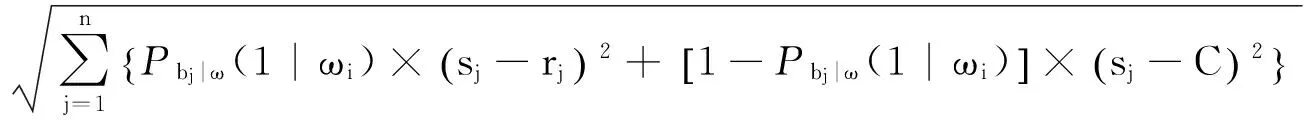
(3)

式(3)中，Pbj|ω(1|ωi)为第i个RP对第j个AP的感知概率，C=-100 dbm为代替未感知到的信号强度情况的数值。

k-NN算法通过选择与实时测量位置距离最近的k个RP点，并计算出这k个RP点对应坐标的均值，即为实时测量位置的估计坐标：

(4)

式(4)，中(xi,yi)'=(xt,yt)为与实时测量位置距离最近的K个RP点的坐标，t为RP点由欧氏距离从小到大排列时对应的前K个RP点的序号为

(5)

2.3 修正最大似然概率算法

为了在复杂环境下获得尽可能好的定位性能，将感知概率引入到贝叶斯估计框架中，并使用直方图统计模型和核密度估计方法进行似然概率计算，提出了基于感知概率的修正最大似然概率算法，具体方案如下：

对于概率型算法，把实测RSS与指纹库中指纹的匹配过程看成概率估计问题，则最大后验概率分布可以描述为：

P(ωi|RSS)>P(ωj|RSS)
i,j=1,2,…,m,j≠i

(6)

式(6)中,ω1,ω2,ω3,…,ωm为离线训练阶段中m个RP的位置信息，RSS为在线测量阶段的接收信号强度。

基于贝叶斯定理，未知参数的后验概率分布可以表示为：

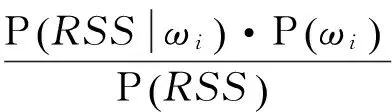
(7)

式(7)中，P(ωi)为对应参考点位置的概率，称之为先验分布密度，P(RSS)为常量。P(RSS|ωi)为给定参考点ωi的数据后的似然概率，各个参考点是相互独立的，并且似然概率相对于参考点而言是唯一的。贝叶斯定理可等价描述为：后验概率分布∝似然函数×先验分布函数。

一般情况下，先验分布密度P(ωi)为根据实践经验在量测实验数据之前确定的，在不考虑定位历史信息的情况下，P(ωi)为常量，因此最大后验概率问题可以转化为最大似然概率问题，即：

P(RSS|ωi)>P(RSS|ωj)
i,j=1,2,…,m,j≠i

(8)

假定各个接入点发出的射频信号之间的影响可以忽略，即各个AP之间是相互独立的，因此可得到似然概率的表达式：

(9)

式(9)中，P(RSSj|ωi)为第i个RP对第j个AP的匹配似然概率。

(1)直方图统计模型

利用直方图统计模型来获得近似的似然概率，离线训练阶段，根据采样数据以及设定的组距得到相应的分组区间，在线阶段，通过判断接收信号所属的分组区间，统计分组区间内可感知样本数目，得到相应的匹配似然概率为：

(10)

则感知似然概率为：

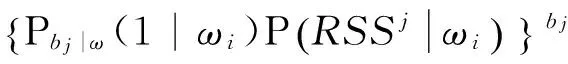
(11)

式(11)中，C=-100 dbm为用来代替未能感知到的信号强度。

(2)核密度估计

采用适合于复杂信号分布的无参数核密度估计方法来计算似然概率，核密度估计方程为：

(12)

式(12)为一个加权平均，而核函数K(·)是一个权函数，核函数的形状和值域控制着用来估计f(x)在点x的值时所用数据点的个数和利用的程度，直观来看，核密度估计的好坏依赖于核函数和核宽参数h的选取。

本文核函数K(·)选定为高斯核函数，如公式(13)所示为：

(13)

由于核宽参数h的取值对基于训练样本的核密度估计曲线的平滑性有较大的影响，所以需要对核宽参数h进行优化选择[11]。本文中通过最小化均方误差来实现核宽参数的优化。

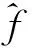
(14)

从积分均方误差的定义式可以看出，被积函数非负，所以上式可改写为：

(15)

假定核方程K(u)连续，真实核密度方程f有界，且二次导数连续。定义两个常数α和β，其中

根据泰勒展开式，MISE可以展开为如下方程：

(16)

因此，最小化均方误差MISE，可以得到核宽参数的优化解为：

(17)

当核函数为高斯方程时，核宽参数的优化解为：

(18)

将感知概率与核密度估计方程结合起来，可以得到第i个RP对第j个AP的感知似然概率为：

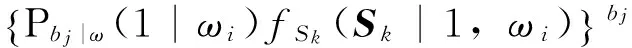
(19)

式(19)中，Sk为设备接收到的第k个AP的实时信号强度，C=-100 dbm为用来代替未能感知到的信号强度。

通过直方图统计模型或者核密度估计方法得到感知似然概率之后，通过ML算法，可求得测量位置的估计坐标为：

(20)

(21)

3 实验及算法性能分析

3.1 实验环境

为了验证修正算法的定位性能，在基于WLAN框架的室内环境下进行验证实验。测试环境位于北航新主楼六层，面积为22 m×14 m的室内区域，主要由房间内区域和走廊区域两部分组成。其中在房间内布置3个符合IEEE 802.11b标准的AP，并将房间区域划分为91个1.1 m×1.1 m的格子；在走廊内布置两个AP，并将走廊区域划分为104个1.2 m×1.2 m的格子。将195个参考点的位置选定为195个格子的中心。实验区域及AP分布如图1所示。

图1 试验区域

在离线训练阶段，对195个参考点分别进行采样，每个参考点采样60次，将60次采样RSS的平均值作为指纹，构成指纹数据库，指纹数据库格式如表1所示。在线阶段，对各个参考点采样20次，并将平均采样值作为实测RSS，用于验证算法性能。

表1 指纹数据库

3.2 实验结果与性能分析

3.2.1 感知概率

室内AP2和室外走廊AP4感知概率分布情况如图2所示。从分布情况可知：对于AP2，室外的参考点(92-195RPs)的感知概率小于1，相反的，对于AP4，室内参考点(1-91RPs)的感知概率小于1。感知概率的分布情况符合信号传播模型，也一定程度上反映了信号强度的分布特性。

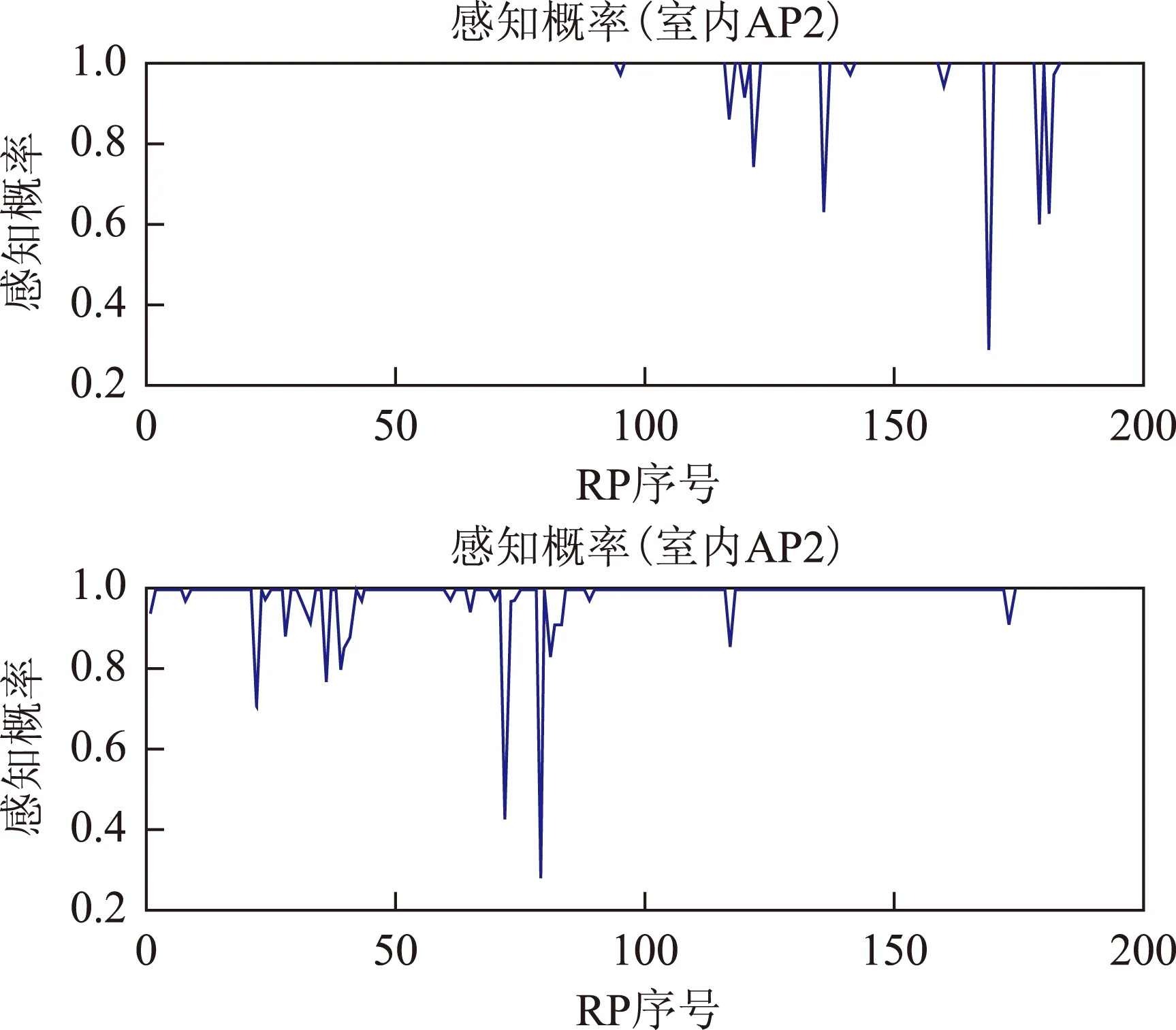
图2 感知概率分布图

根据感知概率的定义，对于感知概率较小的AP，信号有很大的不确定性，可用匹配计算可靠性较低，因此把感知概率引入到现有算法中，可以一定程度上提高定位精度。

3.2.2 修正k-NN算法

对195个参考点进行测试并改变k-NN算法中的k值，以验证修正算法性能。图3为测试位置与真实位置之间误差距离的累积分布函数(cumulative distribution function，CDF)图。

图3 确定型算法误差CDF图

表2列出了不同k值时的算法定位误差结果。当k=3时，修正算法可以达到最好的定位效果，修正wkNN算法的平均误差距离相对于k-NN算法提高了4.3%，修正k-NN算法的平均误差距离相对于k-NN算法提高了6.9%。

表2 定位误差

误差结果分析：由于测试区域简单并且AP信号基本上可以覆盖所有区域，只有少数参考点的感知概率小于1，因此修正算法没有达到最好的定位性能，修正算法对感知概率较小的AP可获得较好的定位精度。

3.2.3 修正ML算法

图4为修正ML算法采用核密度估计技术与直方图统计模型的误差距离的CDF对比图。其中直方图统计模型带宽设为3dBm。修正ML算法采用KDE方法，90%定位误差小于4 m，而采用直方图统计模型相同的定位精度为76%。

图4 概率型算法误差CDF图

核宽参数h对核密度估计的影响大于核函数的选择，对核密度估计曲线有较大影响，图5中实线为核宽参数h取最小均方误差下的最优解时的误差CDF图，表明当核宽参数取最优解时，定位精度有较大提升。

图5 核宽参数对定位精度的影响

4 结论

本文中，首先为了在一定程度上反映信号的分布特征，给出了感知概率的具体定义，然后将

感知概率对欧式距离和似然概率进行加权，提出感知欧式距离和感知似然概率，并将直方图统计模型和核密度估计技术引入到贝叶斯理论框架中，提出确定型k-NN和概率型ML修正算法。通过实验表明，两种修正算法均可以提高定位精度。

[1] KAEMARUNGSI K，KRISHNAMURTHY P.Properties of Indoor Received Signal Strength for WLAN Location Fingerprinting[C]//Proceedings of the First Annual International Conference on Mobile and Ubiquitous Systems：Networking and Services(MobiQuitous'04).Massachusetts：IEEE，2004：14-23.

[2] 邹坤，修春娣，杨东凯.基于感知概率的室内定位系统[J].全球定位系统，2013(6)：7-11.

[3] LI Bing-hao，SALTER J，DEMPSTER A G，et al.Indoor Positioning Techniques Based on Wireless LAN[EB/OL].[2014-08-10].http：//www.gmat.unsw.edu.au/snap/publications/lib_etal2006a.pdf.

[4] ZHOU Mu，XU Yu-bin，MA Lin.Radio-map Establishment Based on Fuzzy Clustering for WLAN Hybrid knn/ann Indoor Positioning[J].中国通信，2010，7(3)：64-80.

[5] SHIN B J，LEE J H，LEE T J，et al.Enhanced Weighted k-nearest Neighbor Algorithm for Indoor Wi-Fi Positioning Systems[J].International Journal of Networked Computing and Advanced Information Management，2012，2(2)：15-21.

[6] 张晓亮，赵平，徐冠青，等.基于一种优化的KNN算法在室内定位中的应用研究[J].电子设计工程，2013，21(7)：44-46.

[7] LEE D J，CAMPBELL M E.Iterative Smoothing Approach Using Gaussian Mixture Models for Nonlinear Estimation[C]//Proceedings of IEEE/RSJ International Conference on Intelligent Robots and Systems(IROS).Vilamoura：IEEE，2012：2498-2503.

[8] ROOS T，MYLLYMAKI P，TIRRI H，et al.A Probabilistic Approach to WLAN User Location Estimation[J].International Journal of Wireless Information Networks，2002，9(3)：155-164.

[9] HAGMANN M，SCAILLET O.Local Multiplicative Bias Correction for Asymmetric Kernel Density Estimators[EB/OL].[2014-08-10].http：//papers.ssrn.com/sol3/papers.cfm?abstract_id=473541.

[10] SHI Xun.Selection of Bandwidth Type and Adjustment Side in Kernel Density Estimation over Inhomogeneous Backgrounds[J].Geographical Information Science，2010，24(5)：643-660.

[11] ALIREZA T，MIRCEA N，GEORGE B，et al.Non-parametric Statistical Background Modeling for Efficient Foreground Region Detection[J].Machine Vision and Applications，2009，20(6)：395-409.