双导航定位系统伪距单点定位数据处理方法与精度分析

高 猛，徐爱功，祝会忠

(辽宁工程技术大学 测绘与地理科学学院，辽宁 阜新 123000)

1 引言

北斗卫星导航系统(BeiDou navigation satellite system，BDS)是中国自主研制开发、具有自主知识产权的卫星导航定位系统，是继美国的全球定位系统(global positioning system，GPS)、俄罗斯的格洛纳斯卫星导航系统(global navigation satellite system，GLONASS)之后，国际上提供定位服务的第3个卫星导航系统[1]。目前已有5颗地球静止轨道(geostationary earth orbits，GEO)、5颗倾斜地球同步轨道(inclined geo-synchronous orbits，IGSO)和4颗中圆地球轨道(medium earth orbits；MEO)卫星在轨运行[2]，BDS已开始向中国及亚太大部分地区正式提供连续无源定位、导航、授时等服务，2020年左右，将建成覆盖全球的BDS[3]。为了测试和验证目前的BDS在伪距单点定位方面的定位精度，本文首先对BDS和GPS联合定位的相关问题进行了阐述，然后进行了BDS、GPS和BDS/GPS伪距单点定位实测数据的处理，最后对测试结果进行了分析。实验结果表明，BDS单系统已经具备了很好的伪距单点定位的能力，但其目前的定位精度仍稍逊于GPS。

2 时间基准与坐标基准

BDS采用北斗时(BeiDou navigation satellite system time，BDT)和CGCS2000坐标系统；GPS采用GPS时(GPS time，GPST)和WGS-84坐标系统。在BDS和GPS联合伪距单点定位中，需要将二者的时间基准和坐标基准进行转换和统一。

BDT和GPST都采用原子时，秒长定义一样，二者都采用周和周内秒计数，不同的是二者的时间系统起算点不同。BDT起始历元为2006-01-01协调世界时(coordinated universal time，UTC)T 00：00：00[4]，GPST起始历元为1980-01-06协调世界时(UTC) T 00：00：00。BDT与GPST二者之间的转换关系为

(1)

CGCS2000坐标系与WGS-84坐标系在原点、尺度、定向及定向的定义是相同的，参考椭球非常相近，唯有扁率有微小差异，由两个坐标系的参考椭球的扁率差异引起同一点在CGCS2000坐标系和WGS-84坐标系内的坐标变化，对于伪距单点定位的影响可忽略，文献[5]指出在坐标系的实现精度范围内，CGCS2000坐标和WGS84坐标一致。

3 数学模型

BDS和GPS的伪距观测方程为

(2)

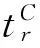
(3)

由式(3)可以得到BDS和GPS的伪距单点定位的误差观测方程

(4)

若测站的近似坐标为(X0,Y0,Z0)、ρ0为卫星到测站近似位置的几何距离、卫星j的对流层延迟误差和电离层延迟误差的近似值分别为T0和I0， 将式(4)用泰勒一阶级数展开后有

(5)

令

(6)

则式(5)可写为

(7)

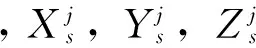
(8)

(9)

在每个历元都可列出一个式(8)和式(9)的误差观测方程组，分别对式(8)和式(9)采用最小二乘方法可以求出未知参数

(10)

(11)

当BDS和GPS联合定位时，对BDS和GPS进行等权处理。将式(8)和式(9)联合使用最小二乘方法可以得到未知参数

(12)

利用每个观测历元的伪距观测值，只要始终保持接收到至少4颗卫星的信号，就能够进行实时的、连续的导航定位。在静态测量定位中，较长的观测时间可以获得大量的多余观测数据，从而可以提高最小二乘解的精度。

4 重要误差源的改正

伪距单点定位的数据处理需要对诸多误差进行改正。影响伪距单点定位的主要误差源有轨道误差、卫星和接收机钟差、对流层延迟误差、电离层延迟误差，相对论效应等误差。

卫星星历是卫星定位中的重要起算数据。卫星轨道误差是指卫星星历中表示的卫星轨道与真正轨道之间的不符值[6]。广播星历的精度相对于伪距单点定位来说，可以忽然轨道误差。卫星轨道位置实质是卫星信号发射时刻卫星的位置。为此，需要根据知道的信号接收时刻即观测数据的记录时间，通过迭代方式计算信号的发射时刻[7]。忽略介质延迟，信号发射时刻ts与接受时刻tr之间有下列关系[7]

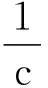
(13)

式(13)中，c为光速，|Xs(ts)-Xr|为接收机至卫星的几何距离，Xr为接收机的近似坐标，Xs(ts)为待求的发射时刻ts的卫星坐标。取ts0=tr-0.075时， 计算卫星坐标Xs0(ts)并带入式(13)计算新的发射时刻。如此反复迭代，直至两次求出的发射时刻相差10-7时，结束迭代过程，最后一次得出的卫星坐标即为所需要的发射时刻的卫星坐标。需要注意的是BDS卫星星座中IGSO和MEO卫星的瞬时位置计算与GPS类似，GEO卫星稍有不同，主要是轨道倾角对同步轨道带来的影响[1]。

卫星钟差的计算需要利用广播星历。广播星历包括卫星钟参数，即表示钟漂移特性的二项多项式

Δts=α0+α1(t-toc)+α2(t-toc)2

(14)

式(14)中，α0、α1、α2为导航电文中的系数，toc为卫星钟差参数的参考时刻。由于接收机一般均采用石英钟，其质量较卫星钟差，所以一般不采用多项式拟合的方法，而是将接收机钟差当做待定参数来处理。

对流层延迟误差是卫星定位中一个重要的误差源，必须妥善加以处理。本文采用WASS对流层延迟模型，WASS对流层模型是与测站的高程、气压、温度、水汽压及温度和水汽压的变化率有关，这些气象参数在任何时刻的值(ξ)可通过下面的经验公式计算出来[5]

(15)

式(15)中，φ是接收机纬度，D是年积日(自1月1日开始计算)，Dmin=28(对于北纬)和211(对于南纬)，ξ0和Δξ的含义分别是测站相应参数的平均值和季节变化量。

平均海平面的天顶干延迟和天顶湿延迟的计算公式分别为

(16)

式(16)中，zdry和zwet分别为平均海平面的天顶干延迟和天顶湿延迟，k1=77.604(k/mbar)、k2=382 000(k2/mbar)、gm=9.784(m/s2)，Rd=287.054(J/kg/k)，p是平均海平面的气压(mbar)，e为平均海平面的水汽压(mbar)，T为平均海平面的温度(K)，β为温度变化率(K/m)，λ为水气压变化率(无单位)。

考虑到测站的高程后，测站的天顶干、湿延迟分别用下面的经验式子计算

(17)

式(17)中，ddry和dwet分别为测站的干天顶延迟和湿天顶延迟，g=9.80 665(m/s2)，H为接收机相对于平均海平面的高度(m)，其他符号与式(16)相同。

利用式(17)计算出测站的天顶干、湿延迟后，总的对流层延迟T0计算公式为二者之和后乘以与卫星高度角(α)有关的投影函数，即

T0=(ddry+dwet)×MF(α)

(18)

式(18)中，MF(α)为将总的天顶延迟投影到适宜的卫星高度角方向上的投影函数。投影函数MF(α)的计算公式为

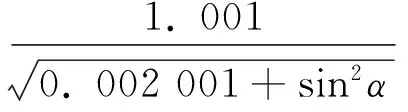
(19)

伪距单点定位中电离层改正普遍采用克罗布歇模型改正公式。该模型将晚间的电离层时延视为常数，取值为5×10-9s，把白天的时延看成是余弦函数中正的部分。于是天顶方向的测距码的电离层改正时延Tg可表示为[9]

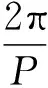
(20)

其中,振幅A和周期P分别为

(21)

式(21)中，αi和βi是地面控制系统根据该天为一年中的第几天以及前5 d太阳的平均辐射流量从多组参数中选取的，然后编入导航电文发给用户。

相对论效应是由于卫星钟和接收机钟所处的状态不同引起的。相对论效应中的常数部分可采用事先将卫星钟的基准频率调低0.00 455 Hz的方法来解决。其非常数部分可用下式进行改正

(22)

(23)

5 实验结果与分析

2012-09-29采用BDS/GPS双系统双频高精度接收机，选用位于37°N、115°E的两个连续运行参考站(continuously operating reference stations，CORS)站的数据进行实验，即测站1和测站2，观测时段为2012-09-29 T 11：39：57-19：17：48，观测历元数为27 472，数据采样间隔为1 s，卫星高度截止角为15°。

笔者进行了BDS、GPS和BDS/GPS上述算法的程序实现，为了对目前的BDS、GPS和BDS/GPS的伪距单点定位情况进行精确的比较，采用PANDA软件处理得到的结果作为准确值，以便后面的定位结果与此进行比较。

测站1和测站2在观测时段内，BDS、GPS和BDS/GPS三种模式下的卫星数变化和PDOP值变化如图1和图2。误差得到处理后，对BDS、GPS和BDS/GPS三种模式进行最小二乘解算，可以得到每个历元在BDS、GPS和BDS/GPS三种模式下的伪距单点定位的结果，与PANDA软件定位结果进行比较，可得到两个CORS站在X、Y、Z方向上的偏差值，如图3和图4。

由图1可以看到，BDS在观测时段内卫星个数为7～9颗，绝大多数时候为8颗。GPS在观测时段内卫星个数为6～10颗，GPS在观测时段内卫星个数变化相比于BDS变化比较大，但大部分时段能保持在6颗以上，在某些时段内，BDS的卫星个数多于GPS的卫星个数，这说明BDS的星座结构已基本形成。BDS和GPS在观测时段内卫星总个数最多时能达到18颗，最少时为14颗，大部分时段能保证在15颗以上。两个测站在观测时段内，BDS和GPS的卫星个数都满足伪距单点定位的要求。

图1 卫星数变化

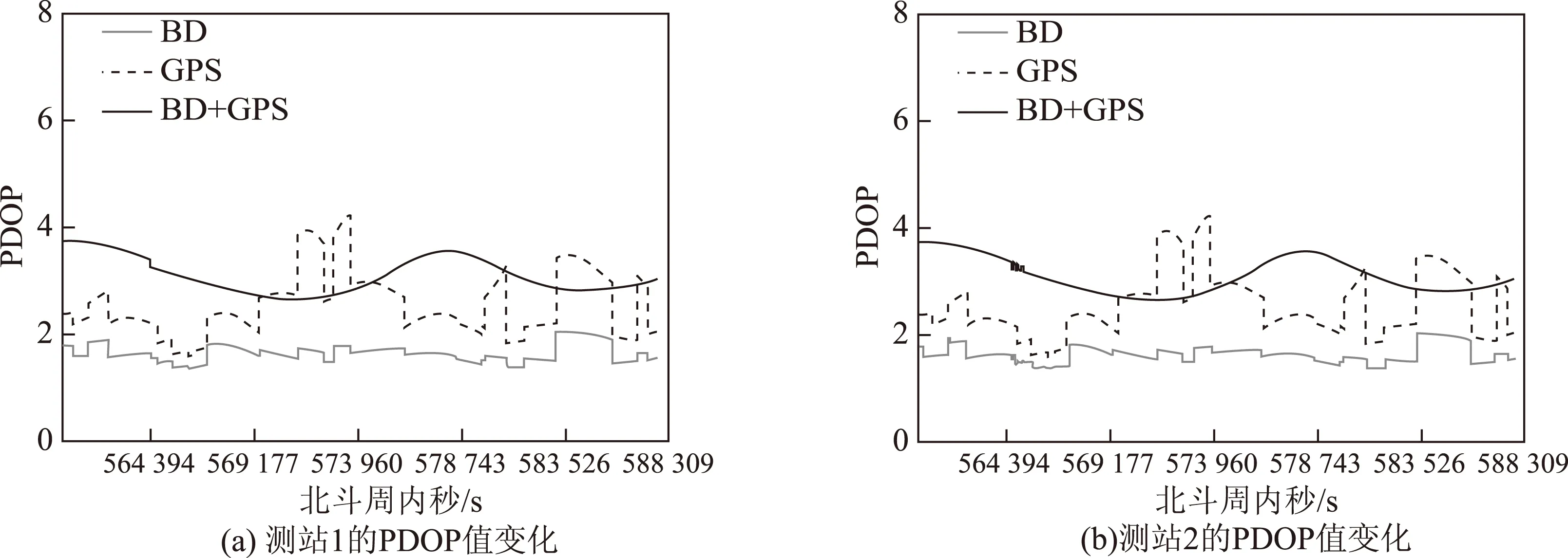
图2 PDOP变化

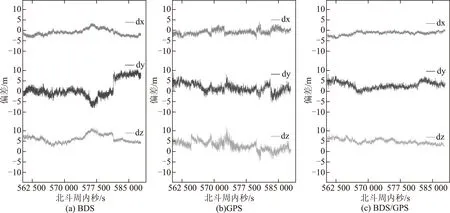
图3 测站1在X、Y、Z方向的偏差

图4 测站2在X、Y、Z方向的偏差

位置精度衰减因子(position dilution of precision，PDOP)值是衡量卫星导航系统定位能力的一个重要指标。由图2可以得到：BDS的PDOP值随着卫星个数的变化在2.8～4之间平稳变化，而GPS的PDOP值变化比较剧烈，但大部分都在1.8～3之间变化，BDS的PDOP值在观测时段内大部分都比GPS高，因此可以认为虽然有些时候BDS的卫星个数超过了GPS，但几何图形强度还是比GPS差。BDS的PDOP值具有一定周期的起伏变化，而GPS的周期性不明显，这与BDS星座采用GEO+IGSO+MEO结构是相符的，其中周期性变化主要由IGSO在地固系中的轨道特点引起。在BDS和GPS联合定位时，其PDOP值明显比两个系统单独情况下都要小，由图2可看到，其PDOP值能平稳的维持在2附近，这说明双系统联合定位增强了定位几何图形。

测站1在BDS、GPS和BDS/GPS三种模式下的定位结果见图3。BDS模式下X方向的偏差最大为3.57 m，大部分偏差都在2.55 m之内平稳变化，Y方向的偏差变化比较剧烈，最大时能达到10.58 m，偏差平均值为2.88 m，Z方向的偏差在1.99 m和11.46 m之间变化；GPS模式下X方向的偏差能保证在2.50 m之内，Y方向的偏差在5.00 m之内，Z方向绝大多数偏差维持在7.55 m以内；BDS/GPS在X、Y和Z方向的偏差变化比较平缓，X方向的偏差优于3.55 m，Y方向的偏差优于5.50 m，Z方向优于7.50 m。由图4可以得到测站2在三种模式下的定位结果。BDS模式下X方向的偏差优于2.50 m，Y方向的偏差最大时达到10.10 m，但大部分历元能维持在7.50 m之内，Z方向的偏差最小时为1.39 m，最大时为11.39 m；GPS模式下X方向的偏差优于2.75 m，Y方向的偏差优于6.25 m，Z方向的偏差优于7.55 m；BDS/GPS模式下X方向的偏差优2.75 m，Y方向的偏差优于6.55 m，Z方向的偏差优于7.50 m。

为了便于定量分析，对BDS、GPS和BDS/GPS三种模式在X、Y、Z方向上的偏差进行概率统计，求出其RMS，列于表1中。由表1可以看出，两测站在BDS模式下的X方向的RMS值优于1.60 m，Y方向优于4.15 m，Z方向优于6.45 m；GPS模式下的X方向的RMS值优于1.28 m，Y方向优于2.50 m，Z方向优于3.65 m；BDS/GPS模式下的X方向的RMS值优于1.45 m，Y方向优于3.15 m，Z方向优于4.90 m。

表1 伪距单点定位的误差RMS值

通过测站1和测站2在三种模式下的定位结果可以看出，BDS可以实现单系统导航定位服务，但目前BDS的伪距单点定位的精度稍逊于GPS。BDS和GPS联合伪距单点定位的精度比BDS伪距单点定位精度高，但稍差于GPS，这可能和BDS的伪距观测数据质量有关。

6 结论

本文分别进行了BDS、GPS和BDS/GPS伪距单点定位实测数据的处理，实验结果表明，目前的BDS伪距单点定位的精度仍稍逊于GPS，BDS和GPS联合伪距单点定位的精度优于BDS伪距单点定位的精度，双系统联合定位增加了卫星的数目和多余观测量，增强了卫星的几何图形强度，当BDS或GPS的卫星个数过少无法定位时，二者组合定位将发挥不可替代的作用。随着后期的BDS卫星的不断发射与系统的完善，BDS定位将更加精确有效。

[1] 高星伟，过静珺，程鹏飞，等.基于时空系统统一的北斗与GPS融合定位[J].测绘学报，2012，41(5)：743-748.

[2] 马瑞，施闯.基于北斗卫星导航系统的精密单点定位研究[J].导航定位学报，2013，1(2)：7-10.

[3] 杨元喜，李金龙，徐君毅，等.中国北斗卫星导航系统对全球PNT用户的贡献[J].科学通报，2011，56(21)：1734-1740.

[4] 中国卫星导航系统管理办公室.北斗卫星导航系统空间信号接口控制文件(公开服务信号B1I)[R].北京：中国卫星导航系统管理办公室，2012.

[5] 魏子卿.2000中国大地坐标系及其与WGS84的比较[J].大地测量与地球动力学.2008，28(5)：1-5.

[6] 叶世榕.GPS非差相位精密单点定位理论与实现[D].武汉：武汉大学，2002.

[7] 魏子卿，葛茂荣.GPS相对定位的数学模型[M].北京：测绘出版社，1988.

[8] 高星伟，程鹏飞，赵春梅，等.WASS对流层延迟模型及其在网络RTK中的应用[J].测绘科学，2011，36(3)：82-84.

[9] 李征航，黄劲松.GPS测量与数据处理[M].武汉：武汉大学出版社，2012.