对流传热系数对沟槽敷设电缆载流量的影响

张周胜，张丁鹏

(上海电力学院电气工程学院，上海 200090)

随着电力电缆线路在城市建设和输配电线路中越来越广泛地应用，电缆更多地使用沟槽敷设方式，尤其在进出配电柜区域，更是得到了广泛运用.为了提高电缆的利用率，充分利用电缆的传输容量，如何根据电缆绝缘的耐受温度来确定电缆载流量成为迫切关注的问题，而准确计算电缆线路的温度场分布正是解决这个问题的关键.［1-4］目前确定电缆载流量的方法有两种，即根据IEC60287解析计算和数值计算.［5］

根据IEC60287的解析计算，可以用比较简单的数学公式近似地计算出电缆的载流量，但是这种方法仅能够解决一些相对简单的问题.［6］数值计算则是在给定负荷条件、电缆敷设、排列条件等情况下，对整个电缆周围的温度场进行仿真分析，更加准确并接近实际情况.因此，在面对较为复杂的敷设情况或者电缆群，数值计算拥有更大的灵活性，其计算结果也更为准确.［7-9］

但在数值计算中，许多客观条件因素对载流量有较大的影响，如敷设方式、土壤湿度、环境温度、对流换热系数α等.另外，在不同的文献中，对流换热系数α取值也不一样，例如:谢光彬等人［10］选用8.7/15kV YJV400mm2单芯交流聚乙烯绝缘聚氯乙烯护套电缆土壤直埋敷设为例时，对流换热系数取值为5.3;梁永春等人［11］选用800mm2YJLW02XPLE电力电缆在土壤中排管敷设为例时，对流换热系数取值为12.5;而同样是梁永春等人［12］在另一篇文献中以400mm2YJLW02XPLE三芯电力电缆局部穿管敷设为例时，对流传热系数仍取值为12.5;程子霞等人［13］选用电气化铁路27.5kV单相单芯交联聚乙烯电缆时，对流传热系数取值为10.对此笔者发现，对流传热系数在采用不同的型号电缆不同敷设条件时，取值完全不同，电缆同型号而敷设方式不同时，也有可能取值一样，而相关文献中并没有针对对流换热系数的计算过程.本文通过选取不同的α值，利用有限元仿真模拟温度场配合弦截法得到载流量，对比α不同取值与相应的载流量的变化，观察α的变化对载流量的影响.最后利用经验公式，提出了对流换热系数的合理计算方法，通过实际计算确定一个较为准确的对流换热系数α，并确定对应的载流量.

1 对流换热系数

流体流过固体表面时流体与固体间的热量交换称为对流传热，流体与固体表面之间的换热能力，称为对流换热系数.当电缆直埋敷设于土壤中时，空气作为流体与地表的土壤进行换热，这时的换热能力则用对流换热系数来表示.

对流传热的换热量用牛顿冷却公式计算，单位面积对应的热流密度为:

式中:α——对流换热系数;

Δt——温差，℃.

对于面积为A的接触面，对应的热流量为:

式中:Δtm——换热面A上流体与固体表面的平均温差.［14］

牛顿冷却公式只是对流换热表面传热系数α的一个定义式，它没有揭示出表面传热系数与影响它的有关物理量之间的内在联系，而在传热学中，流体与固体对流换热系数使用的经验公式为:

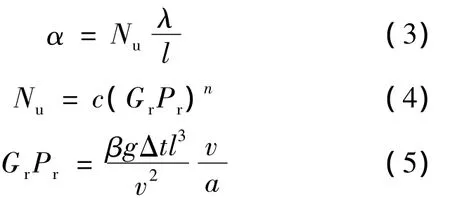
式中:Gr——格拉晓夫数;

Pr——普朗特数;

β——体积膨胀系数;

l——线性尺寸，m;

v——运动粘度，m2/s;

Nu——努赛尔数;

c，n——系数;

a——热扩散率.

其中，对于理想气体:

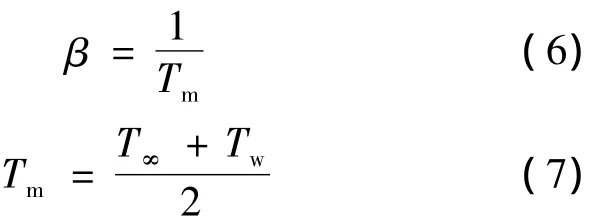
式中:Tw——分界面温度;

T∞——不受分界面温度影响的温度.

2 温度场模型理论基础

地下电缆群的稳态温度场是一种二维稳态导热问题.有热源区域的温度控制方程为:

式中:T——场域内(x，y)点温度，K;

qv——体积发热率，W/m3.

无热源区域的温度控制方程为:

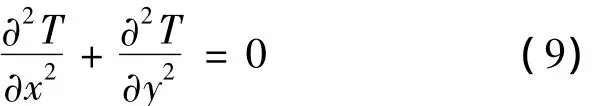
传热问题的边界条件可归结为3类.第1类边界条件为已知边界温度;第2类边界条件为已知边界法向热流密度;第3类边界条件为对流边界条件，即知道对流换热系数和流体温度.3类边界的控制方程分别如下:

式中:Γ1，Γ2，Γ3——分别为第 1 类、第 2 类和第 3类边界条件线;

λ——导热系数，W/(m·K);

q2——热流密度，W/m2;

Tf——流体温度，K.

利用加权余量法和Galerkin法对式(10)、式(11)和式(12)进行处理，得出相应的线积分方程如下:

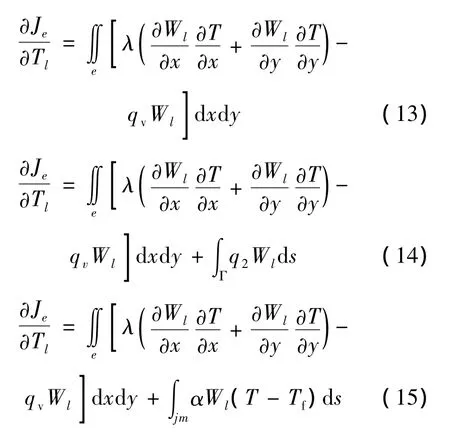
式中:l=i，j，m.

求解式(13)、式(14)和式(15)，并对整个区域整体合成，得:

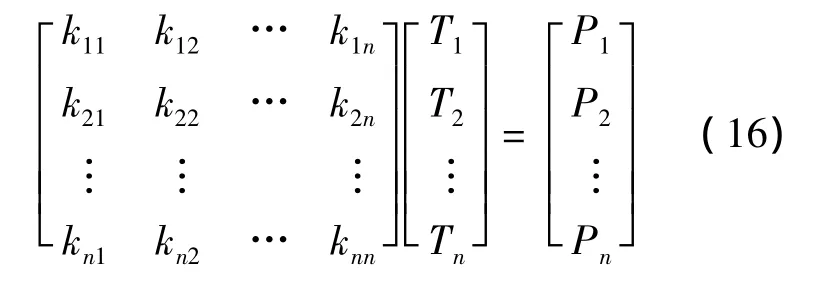
式中，kij，Pi可利用三角面积积分进行计算;n 为剖分节点数;i，j=1，2，3，…，n.［15］

利用迭代法或高斯法对式(16)求解，即可求得各点的温度值.

3 电缆温度场模型

以单芯电缆双回路电缆沟直埋敷设方式为例，建立电缆群温度场模型，如图1所示.电缆群直埋电缆沟中，周围填充细沙.

整个区域近似于半无限大温度场.需要将一个半无限大区域场转变为闭域场才能进行求解.温度在电缆附近变化较为明显，当离电缆较远时，土壤温度则视为等温面，尤其是土壤深层温度不随表面温度的变化而变化.本文中左边界和右边界取距离最近电缆1 500mm的直线，下边界取距离最近电缆2 000mm.将电缆沟模拟成如图1的闭域场.图1中，深层土壤边界(下边界)为第1类边界条件，使用式(3)边界方程;左右土壤为第2类边界条件，使用式(4)边界方程;地表面为第3类边界条件，使用式(5)边界方程.在第3类边界条件方程中，就需要使用到对流换热系数和空气温度.

图1 单芯双回路电缆电缆沟敷设方式示意

4 载流量的计算

一般采用弦截法计算载流量，求解公式为:

计算步骤如图2所示.

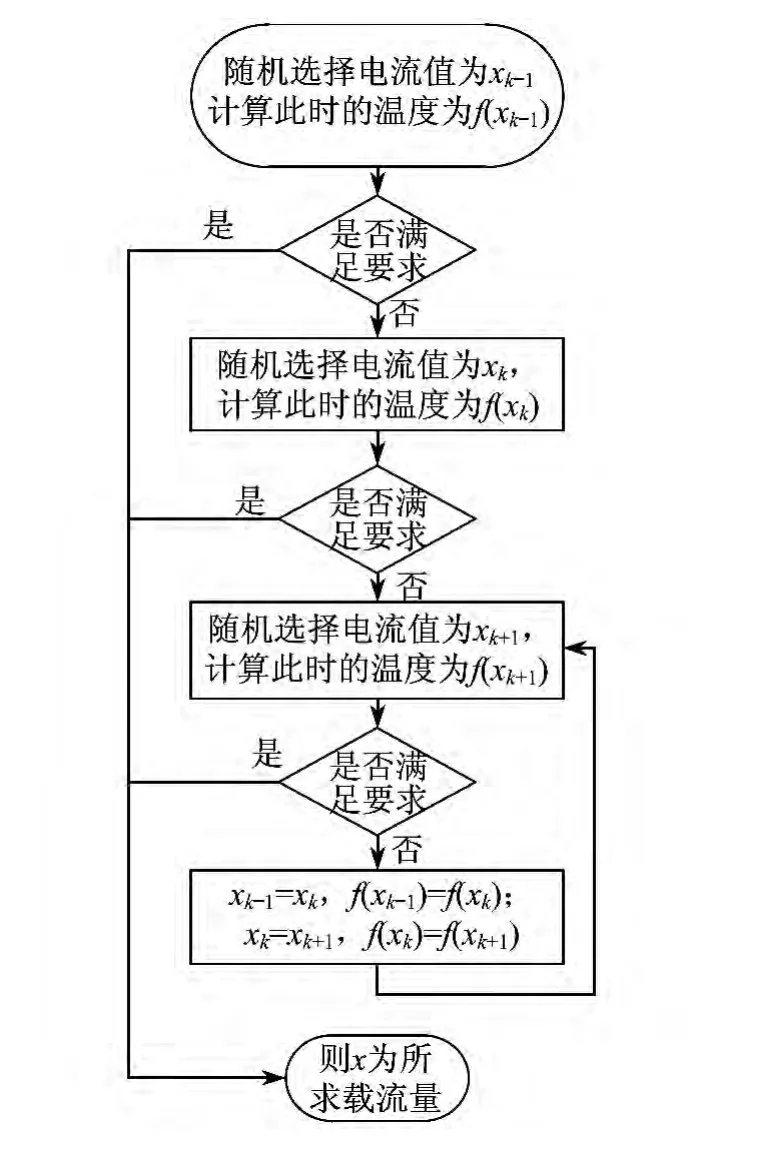
图2 弦截法计算步骤

需要注意的是，f(xk-1)，f(xk)，f(xk+1)分别为电流xk-1，xk，xk+1利用有限元计算所得导体温度减去363 K(交联聚乙烯电缆长期工作寿命下的绝缘耐受温度)后的所得值.

5 对流换热系数对载流量的影响

5.1 电缆和敷设参数

以800mm2YJLW02XPLE电力电缆，单芯电缆双回路电缆沟直埋敷设为例，电缆结构参数见表1，敷设条件见表2.

表1 电缆结构参数mm

表2 电缆群敷设参数 K

5.2 对流换热系数对电缆最高温度的影响

对流换热系数α在6～12间取值，以1/3为间隔，假定载流量为870 A，利用有限元法仿真出电缆最高温度，将得到的结果绘制成直角坐标图，如图3所示.

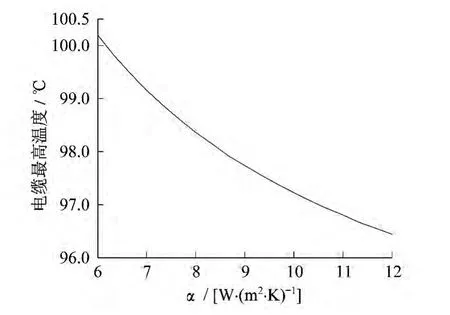
图3 不同对流换热系数对应的最高温度

由图3可知，在额定载流量、环境温度为35℃的情况下，对流换热系数α对埋地敷设电缆最高温度的影响呈现非线性，有递减的趋势.随着α的增大，空气与土壤的换热能力增强，因此土壤中电缆的最高温度也随之降低.

5.3 弦截法计算载流量

利用弦截法，计算出不同的对流换热系数α的值对应的实际载流量，将得到的结果绘制成直角坐标图，如图4所示.

由图4可见，在额定载流量、环境温度为35℃的情况下，对流换热系数α对埋地敷设电缆的载流量的影响也呈现非线性，有递增的趋势.随着α的增大，空气与土壤的换热能力增强，因此土壤中电缆的最高温度也随之降低，对应的载流量随之升高.

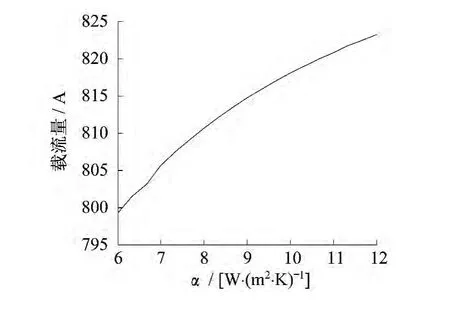
图4 不同对流换热系数对应的载流量

6 对流换热系数的计算

由图3与图4可知，对流换热系数α对载流量有比较大的影响.随着α的增大，载流量也会升高.其具体的取值会导致不同的载流量结果.为了充分利用电力电缆线路的传输容量，提高电缆的利用率，α准确地取值具有举足轻重的作用.本文针对集合电缆及敷设方式，分析了α的合理计算过程.

式(6)中，T∞为 298.15 K，Tw为 308.15 K，因此其平均温度 Tm为335.65 K，即62.5℃，查表［14］所得大气压力下62.5℃干空气热物理性质分别为:

计算得出Gr为4.88×106，根据均匀壁温边界条件的大空间自然对流中常数c和n的实验数值表可知，流态方式为层流，c和n应分别取值为0.59 与 0.25.

根据经验公式计算确定 α 为7.1 W/(m2·K)，利用有限元法仿真计算后，得到此时载流量为806.21 A.

7 结论

(1)在相同条件下，随着对流换热系数α的增大，直埋敷设电缆中最高温度随之降低，呈现非线性，直埋敷设电缆中载流量随之升高，也呈现非线性;

(2)针对800mm2YJLW02XPLE电力电缆单芯双回路直埋敷设方式中，对流换热系数α应取值为7.1 W/(m2·K)，此时对应的载流量为806.21 A.

［1］ 梁永春，王忠杰，刘建业，等.排管敷设电缆群温度场和载流量数值计算［J］.高电压技术，2010，26(3):763-768.

［2］ HWANG C C.Calculation of thermal fields of underground cable systems with consideration of structural steels constructed in a duct bank［J］.IEE Proceedings Generation，Transmission and Distribution，1997(6):541-545.

［3］ 付永长，张文斌，陈涛，等.不规则排列电缆温度场及载流量计算［J］.电网技术，2010，34(4):173-176.

［4］ 郑雁翎，王宁，李功杰，等.电力电缆载流量计算的研究和发展［J］.电线电缆，2010(2):4-9.

［5］ 梁永春，赵静，闫彩红.沟槽电缆温度场和载流量的数值计算［J］.高电压技术，2012，38(11):3 048-3 053.

［6］ 梁永春，李延沐，李彦明，等.利用模拟热荷法计算地下电缆稳态温度场［J］.中国电机工程学报，2008，28(16):129-134.

［7］ 鲁志伟，于建立，郑良华，等.交联电缆集群敷设载流量的数值计算［J］.高电压技术，2010，36(2):481-487.

［8］ 曹慧玲，王增强.坐标组合法对直埋电缆与土壤界面温度场的数值计算［J］.电工技术学报，2003，18(3):59-65.

［9］ 郑良华，于建立，周晓虎，等.直埋电缆群载流量和稳态温度场计算新方法［J］.高电压技术，2010，36(11):2 833-2 837.

［10］ 谢光彬，谢伟.基于温度场的单芯电缆载流量研究［J］.四川电力技术，2010，33(1):86-88.

［11］ 梁永春，闫彩红，赵静，等.排管敷设电缆群暂态温度场和短时载流量数值计算［J］.高电压技术，2011，37(4):1 002-1 007.

［12］ 梁永春，王巧玲，闫彩红，等.三维有限元法在局部穿管直埋电缆温度场和载流量计算中的应用［J］.高电压技术，2011，37(12):2 911-2 917.

［13］ 程子霞，薛文彬，周远翔，等.电气化铁路27.5kV单相单芯交联聚乙烯电缆载流量计算［J］.高电压技术，2012，38(11):3 067-3 073.

［14］ 杨世铭，陶文铨.传热学［M］.第4版.北京:高等教育出版社，2006:43-52.

［15］ 孔祥谦.有限单元法在传热学中的应用［M］.第3版.北京:科学技术出版社，1998:121-133.