PEEC在铁磁板低频磁场屏蔽效应计算中的应用

夏能弘，郭 杰，田孟林，周歧斌，姜恩宇

(1.上海电力学院，上海 200090;2.上海市防雷中心，上海 201615)

有关低频磁场屏蔽问题的研究已经有很多，［1-3］大部分研究工作的关注对象主要包括线结构、板结构以及圆柱形外壳结构.其中，平板结构常用于建筑中，通过遮挡或屏蔽来构筑电磁兼容的空间.屏蔽板的材料一般包括铁磁性材料和非铁磁性材料.

为了对金属板的屏蔽效能进行评估和比较，有效的数值计算工具十分必要.目前，已有多种成熟的数值计算方法可用于处理复杂几何结构的电磁问题.其中，部分元等效电路法(Partical Equivalent Electrical Circuit，PEEC)由于其对电气互联结构的全波计算能力，受到了广泛关注.［4-6］该数值方法可将电磁场问题转换到电路领域进行分析，使电磁场的场作用机理更容易理解.

对于3D电磁场数值分析，PEEC方法的一个重要制约因素是对象经离散后会产生大量体积元或面元，且在多对象共存的情况下尤为显著.因此，对PEEC模型进行优化、降低计算成本、减少求解时间是非常有意义的工作.其中，减少待求解未知数的数量是一种十分有效的途径.

本文提出了一种基于PEEC的电磁场对称建模方法，该方法只需对原始对象的一部分进行计算.本文中假定对象金属板由线性磁性材料制成.首先，根据经典PEEC理论，对整块铁磁板结构建立PEEC模型.然后，对分布于金属板上的电磁物理量进行分析，考察各对称部分的电磁分量的分布规律，分析它们的对称和反对称关系.根据这些规律，对已建立的PEEC模型进行改进，即可得到对称模型.随着未知量的大幅减少，求解矩阵的尺寸也随之大幅压缩，对计算资源的需求显著降低.这种改进的3D电磁建模技术可用于求解更复杂的3D结构.

1 等效电路法

本文主要研究铁磁金属板对由外部载流线激发的低频磁场的屏蔽作用.金属板和电源线之间的互耦作用通过一组相互耦合的电路元件模拟.金属板中的涡电流可通过PEEC法来求解.板周围空间的磁场则可由外部电流源及板中次生的涡流叠加产生.模型结构如图1所示.

图1 模型结构的剖面示意

外部电流源是一个由细丝导体构成的方形回路，交流电流在其上循环流动.薄金属板放置于电流源上方，起磁场屏蔽作用.金属板由线性磁性材料制成，其相对电导率为σ，相对磁导率为μr.由于该板的厚度比平面尺寸小得多，故可以认为该板的涡流在厚度方向的分量可忽略不计，即该板中的涡流方向为切线方向.

1.1 电场积分方程

PEEC方法源于电场积分方程，该方程表明了在空间r点处，矢量磁位A(r)与标量电势φ(r)的关系，即为:

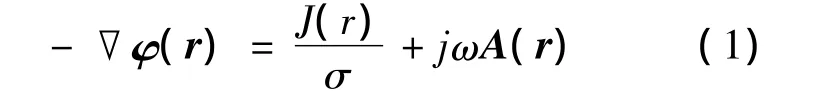
式中:J(r)——涡流电流密度.

由于该屏蔽板为磁性材料，板本身磁化所产生的矢量磁位也需要加以考虑.因此，总的矢量磁位为 A(r)=Ac(r)+Am(r)+As(r).式中，Ac(r)由涡流电流产生，Am(r)由磁极化产生，As(r)则来自于外部电流源.

式中:r，r＇——考查点和作用源的位置矢量.

重写式(1)，可得到一个新的电场积分方程为:

式中:ΔUl——沿着l线段的电势差.

1.2 几何离散

为了进行数值计算，首先必须进行几何离散，即将铁磁板剖分成众多微体积元，称为势单元.图2给出了势单元的平面排列图.

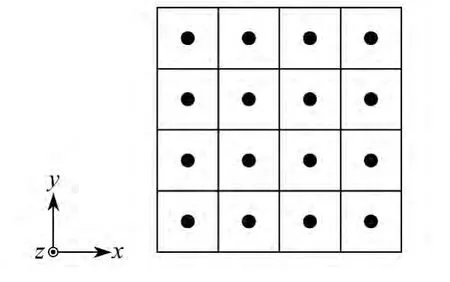
图2 势单元的平面排列示意

在一个平面上有NX×NY个势单元(NX和NY分别表示x轴和y轴方向上的势单元数).由于涡流电流在相邻的势单元之间流动，因此这里规定电流单元形成于相邻两个势单元的中心点之间.对涡电流进行正交分解，这些电流单元可分为两类:X电流元和Y电流元，如图3所示.它们的数量分别为Nx=(NX-1)NY和Ny=NX(NY-1).

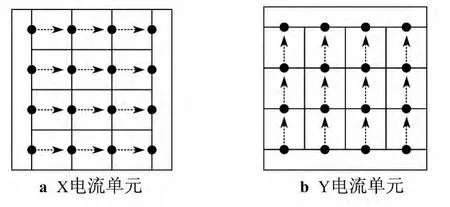
图3 离散后铁磁板上的部分单元

假定每个单元中的涡流电流密度和磁化强度是恒定不变的，则支路电压方程可重新定义为:

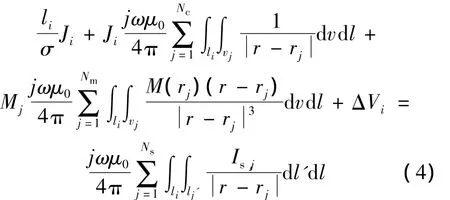
式中:Nc，Nm，Ns——电流单元、势单元、电流源的数量.

此外，作为式(4)的补充条件，在任意节点均可建立电流平衡方程，即KCL方程，如图4所示.图4中节点的KCL方程为:

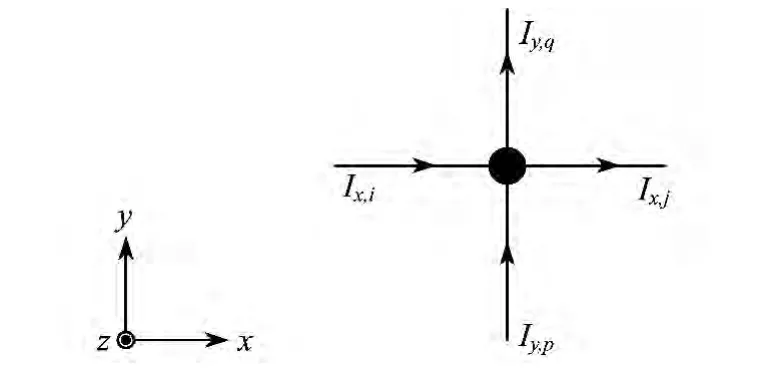
图4 节点处的KCL

另外，由矢量磁位A(r)与磁通密度B的关系B(r)=▽(Ac(r)+As(r)+Am(r))，可得到磁化强度M的方程为:

涡流电流密度J和磁化强度M均可作正交分解，得到 Jx，Jy和 Mx，Mx，Mz.因此，式(4)和式(6)就可以分别分解成2个和3个方程.

1.3 PEEC 3D模型的建立

结合式(4)、式(5)和式(6)，可得到完全求解矩阵如下:

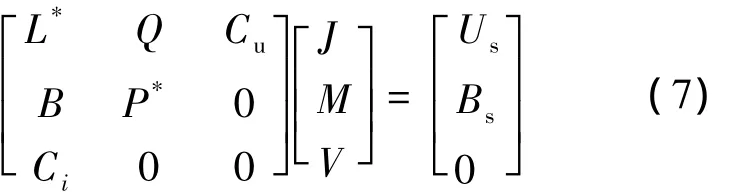
式中，Cu将节点电势转换为支路电压，Ci反应了在节点处各支路电流之间的关系.矩阵中其他参量的计算详列如下:

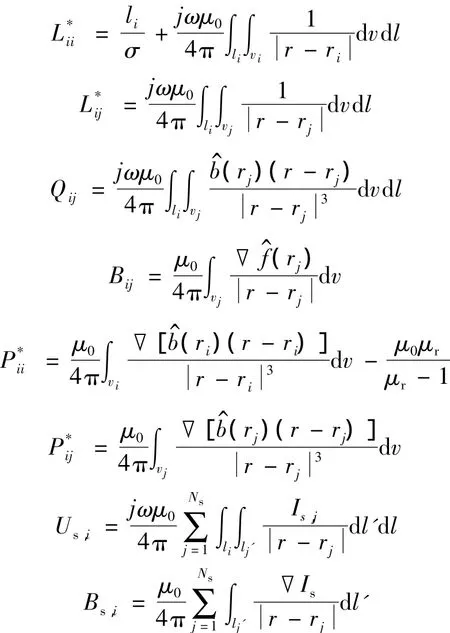
去掉一个电势参考点，各未知参量V，J，M的数量分别为NV=NXNY-1，NJ=NXNY-NX-NY，Nm=3NXNY.因此，总的未知量的数量为 Ntot=6NXNY-NX-NY-1.

借助数学工具可以很容易地求解式(7).然而当研究对象比较复杂且未知量数量相当庞大时，建立和求解该矩阵方程会非常困难.

1.4 屏蔽后磁场的计算

求得涡流电流密度和感应磁场后，即可估算铁磁板的屏蔽效能.铁磁板周围空间的磁场B的计算方法如下:

1.5 对称结构的建模

在对称结构中，各对称部分的涡电流分量和磁化强度分量的分布具有对称性或反对称性，即:不同部分的电磁分量可能幅值相同，方向相反.另外，由于整个结构被等效为互连的电路网络，式(7)中的某些子矩阵可以被折叠和重新组合，这将大大减少未知量的数量.

图5为铁磁板上涡流和磁场分布的示意图.其中，涡电流循环流动形成闭合回路，磁场则有规律地穿透铁磁板.

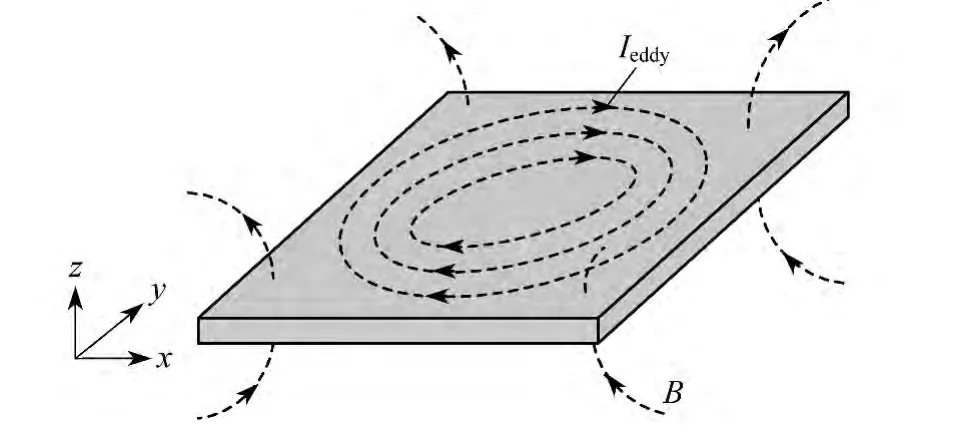
图5 铁磁板的涡流和电磁分布

铁磁板上各对称部分电磁分量之间的关系如图6所示.

图6 铁磁板上各对称部分电磁分量之间的关系

由图6可知，铁磁板被分成4个部分.各分量的具体关系如下:

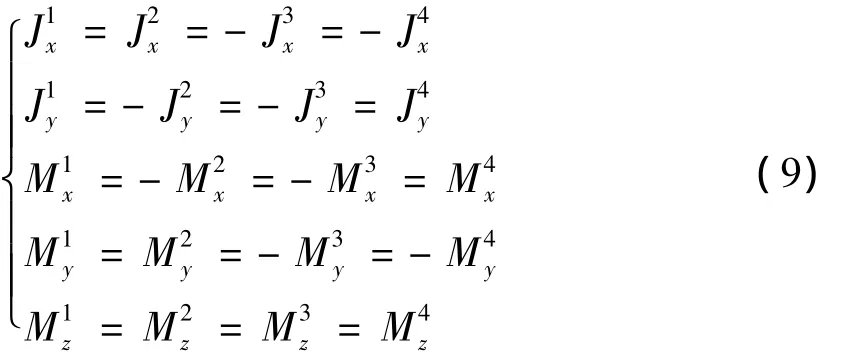
只考虑分块①中的电流密度Jx，则有:

将式(9)代入式(10)，可得:

式中:

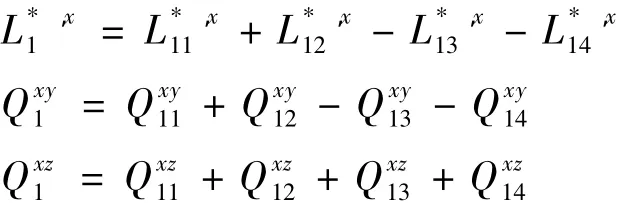
同样，式(7)中的其他参数被压缩如下:

未知量V1，J1，M1的数量分别为因此，总的未知量数量为 Ntot=1．5NXNY．

2 数值验证

数值验证的结构如图1所示.其中，薄铁磁板为线性铁磁材料制成，其电导率σ=0.75×107S/m，相对磁导率μr=200.激励电流源为交流1 A，50 Hz的细丝状方形载流环路，其尺寸为:w=200 mm，d=2 mm，h=50 mm.采用非均匀网格剖分(Nx=54，Ny=54).表1列出了原始求解矩阵式(7)和改进后的求解矩阵式(12)的计算信息.

表1 未知数个数及矩阵大小

在Matlab环境中开发相应的计算程序.以基于边界元法的商用软件IES-FARADAY作为参考，对结果进行比较，结果如图7所示.大部分区域的计算结果与参考值较为符合，靠近边缘的部分出现微小误差，其中Jy和Mx的最大误差分别为4.13%和3.37%.沿板上方对角线的磁感应强度B的2个分量如图8所示，最大误差仅为2.4%.

图7 铁磁板底部中线(y=0，z=49mm)处计算结果

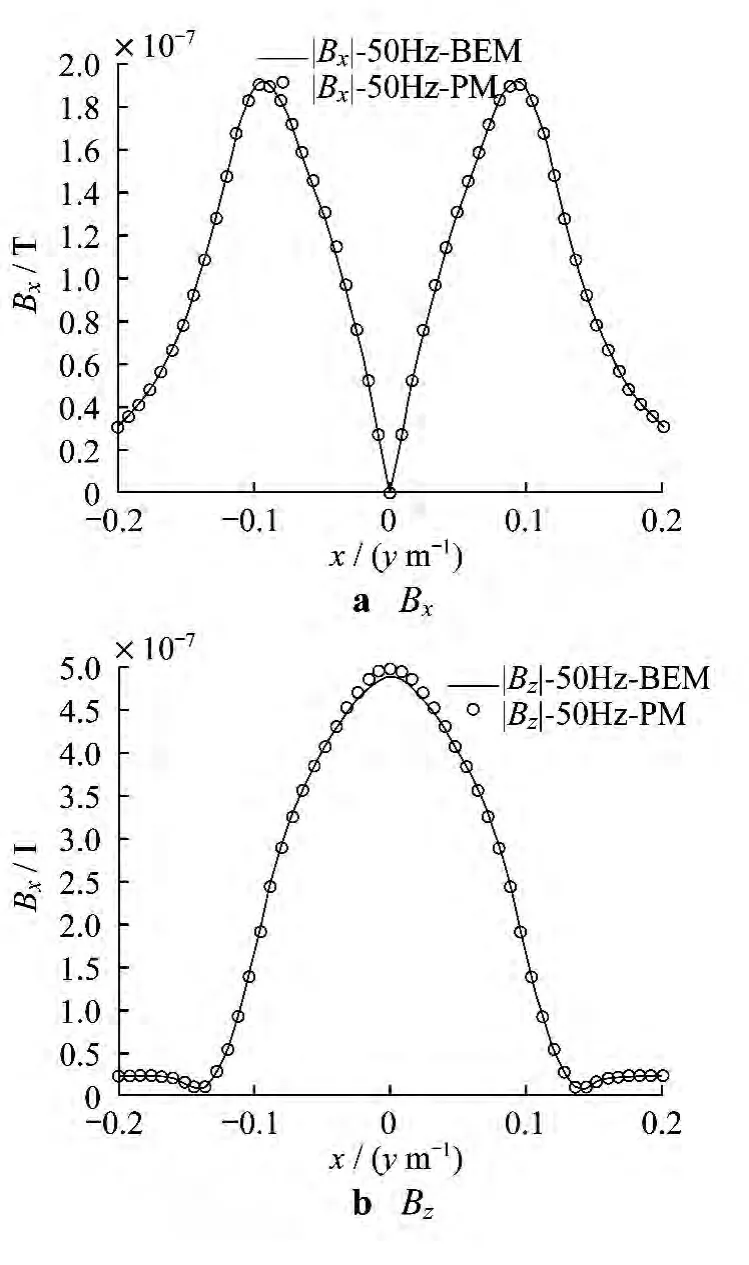
图8 对角线上磁感应强度B的计算结果(z=100mm)

3 结语

本文建立了用于评估铁磁板低频磁场屏蔽效能的三维PEEC模型.由于涉及磁性材料，将经典电场积分方程与磁场方程进行整合，得到针对磁性结构的完整方程组，可求解涡电流和磁化强度.针对对称结构，对原始模型进行改进，所得模型的未知量数量大幅减少.对该计算方法进行数值验证，结果表明该方法在评估低频磁场屏蔽方面具有较高的精度，效率较边界元法提高了4倍.这种方法还可进一步扩展以求解更复杂的结构.

［1］ BINNS K J，LAWRENSONP.J.Analysis and computation of electric and magnetic field problems［M］.New York:Pergamon Press Ltd，1977:123-127.

［2］ BURNETTJ Duy.ELF shieldingperformance ofmetallic enclosure for heavy-current conductors［J］.IEEE Proc.-Gener.Transm.Distrib，1999(3):223-228.

［3］ ISTENICM，OLSENR G.A simple hybrid method for ELF shielding by imperfect finite planar shields［J］.IEEE Trans on EMC，2004，46(2):199-207.

［4］ RUEHLIA E.Equivalent circuit models for three-dimensional multiconductor systems［J］.IEEE Trans.Microwave Theory Tech.，1974(22):216-221.

［5］ RUEHLIA E，HEEBH.Circuit models for three-dimensional geometrices including dielectrics［J］.IEEE Trans.Microwave Theory Tech.，1992，40(7):1 507-1 516.

［6］ RUEHLIA E，GARRETTJ，PAULC.Circuit models for 3-D structures with incidentfields ［J］.IEEE Int.Symp.Electromagn.Compat.，1993(8):28-32.