20辊森吉米尔轧机辊系运动学分析与计算

陈 洁

（中冶南方工程技术有限公司技术研究院，湖北 武汉430223）

20辊森吉米尔轧机是高精度轧制核心设备之一，具有道次压下率大、轧制力小、运行成本低、辊系变形小等特点，应用十分广泛。森吉米尔轧机具有多种调整机构。在轧制过程中，通过手动或自动控制系统，获得高精度的、板形优良的成品带材［1］。本文以某森吉米尔轧机辊系为研究对象，对辊系进行运动学分析，并计算出轧机调整关系曲线，为板带轧制工艺优化、板型调整提供参考。

1 辊系结构分析

20辊森吉米尔轧机的辊系呈塔形布置（图1）于机架梅花膛孔内，上下对称。工作辊S、T分别支撑在两个第一中间辊O、P、Q、R上；第一中间辊又分别支撑在第二中间辊I、J、K、N、M、L上；第二中间辊则靠8个支撑辊A、B、C、D、E、F、G、H 来支撑。每个支撑辊由数个背衬轴承和鞍座安装在同一根轴上。其中A、D、E、H为轧机的侧偏心补偿辊，用于轧辊磨损后的辊径补偿；B、C为轧机压下及AS－U－ROLL调整辊，用于压下调整及凸度调节；F、G则为轧制线标高调整辊，保证带钢始终处于轧制线上。8根支撑辊的轴心与机架梅花孔心均存在一定的偏心量，通过旋转支撑辊的偏心，使支撑辊芯轴产生一定的位移，从而实现轧辊相对位置的调整。这种控制调整具有快速、准确等优点，保证带钢的轧制精度要求。

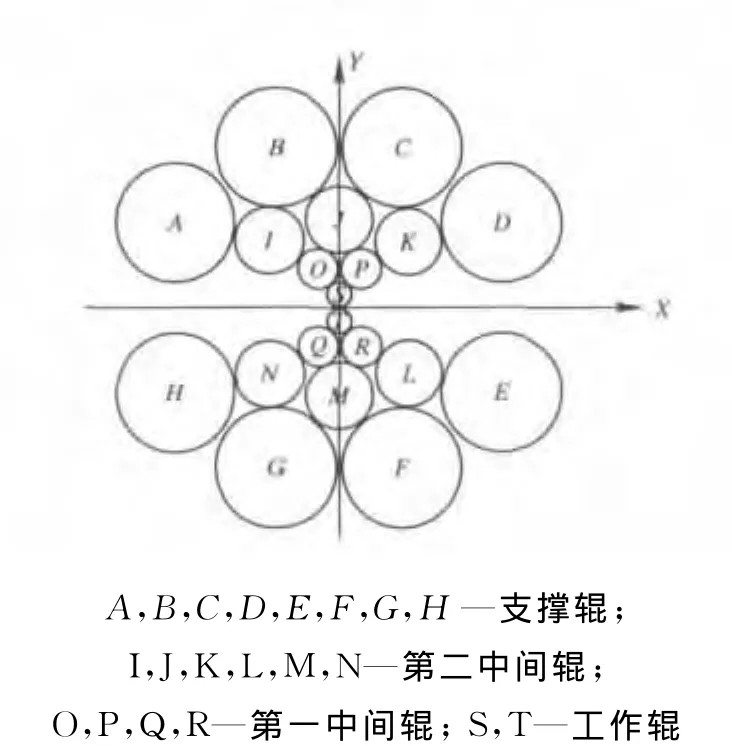
图1 20辊森吉米尔轧机辊系图

工作辊之间、第一中间辊彼此之间、第二中间辊彼此之间以及支撑辊彼此之间不能接触。第二中间辊I、K、N、L为传动辊，其余各辊靠辊间摩擦力转动。辊系参数如表1所示。

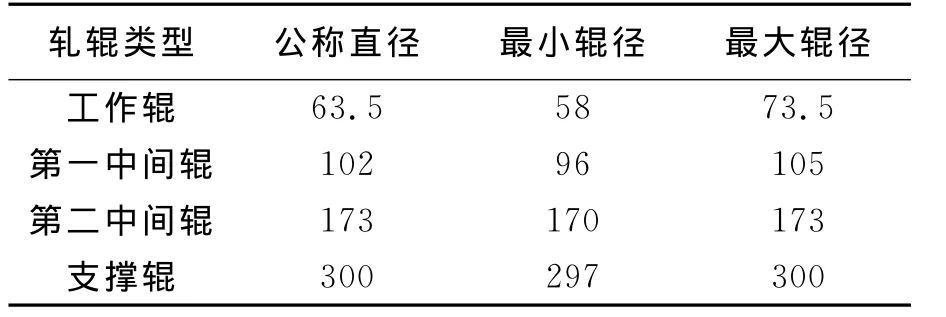
表1 20辊森吉米尔轧机辊系参数 mm

2 辊系运动学模型

将辊系简化成杆系，连杆两端点分别为轧辊的辊心，连杆长度即为两轧辊半径之和［2］。由于该轧机辊系为平面对称分布，可取其1／4进行分析；根据约束条件，将二中间辊J和工作辊S圆心处简化为滑块机构。根据辊系简化图（图2），可得辊系运动学分析向量图（图3a）和标量图（图3b），图3b中r1～r13为图3a中各向量的长度，θ1～θ13为这些向量的角度。

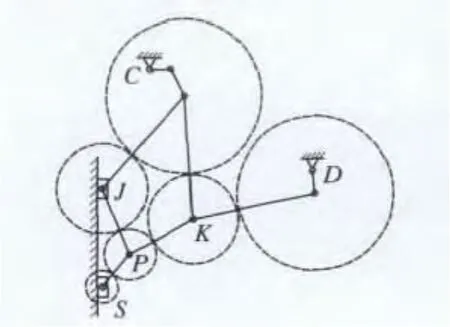
图2 20辊轧机辊系简化图

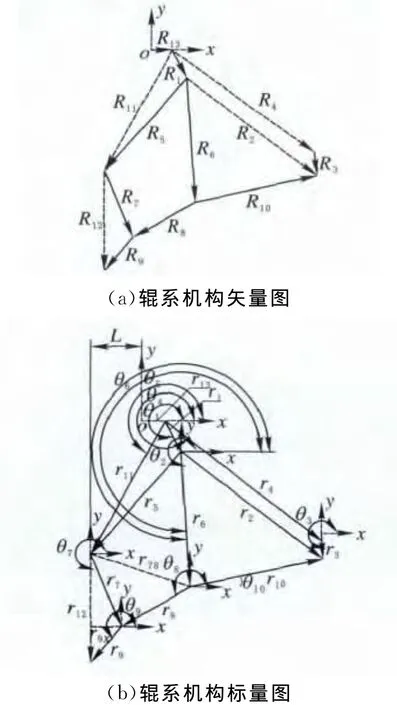
图3 辊系运动学分析

以C辊鞍座环中心为坐标原点，由图3b可得闭环矢量方程［3］

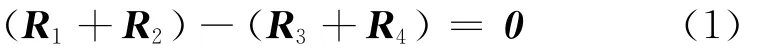
将式（1）转化为标量形式

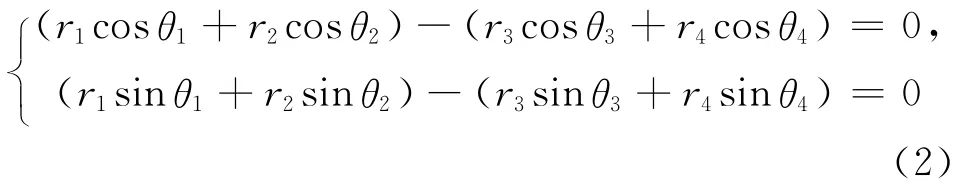
因为支撑辊C辊和D辊鞍座环的圆心坐标已知，且r13＝1.016，θ13＝0，因此r4和θ4可求出。又已知r1＝6.35，r3＝3.175，若给定θ1和θ3，即由式（2）求出r2和θ2。

同理，由图3b可得闭环矢量方程

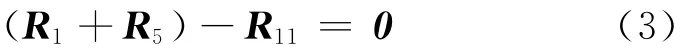
将式（3）转化为标量形式

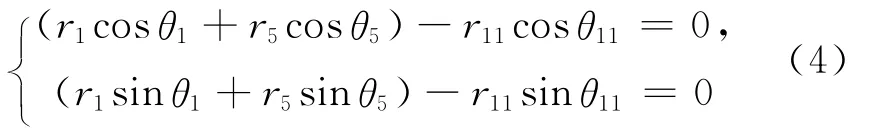
根据辊系左右对称的特性，J辊辊心必须在机架垂直中心线上。令L为支撑辊C辊鞍座环中心与机架垂直中心线的距离，因此r1cosθ1＋r5cosθ5＝L＋r13。已知L＝149.225和r5，则θ5可求出。因此r11和θ11可求出。即第二中间辊惰辊J辊的辊心坐标可求。

由图3b 可得闭环矢量方程

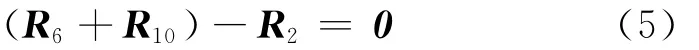
将式（5）转化为标量形式

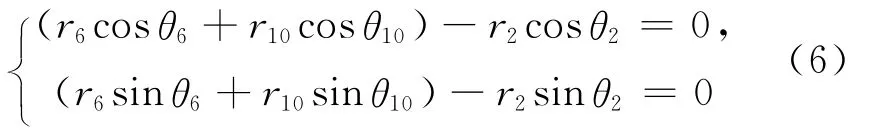
已知r2、r6、r10及θ2，利用牛顿－辛普森法，可求出θ6和θ10。即第二中间辊传动辊K辊的辊心坐标可求。

由图3b可得闭环矢量方程

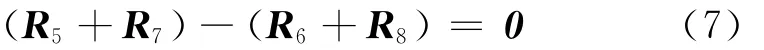
将式（7）转化为标量形式

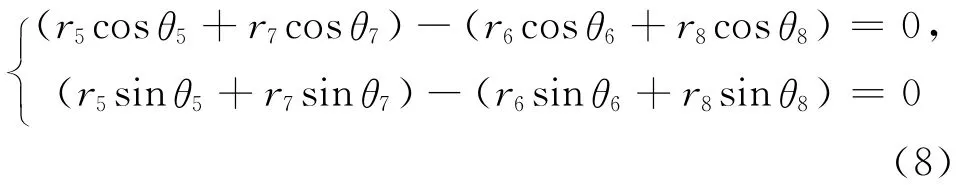
已知r5、r7、r6、r8及θ5、θ6，利用牛顿－辛普森法，可求出θ7和θ8，即第一中间辊P辊的辊心坐标可求。

最后，由图3b可得闭环矢量方程

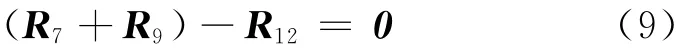
将式（9）转化为标量形式

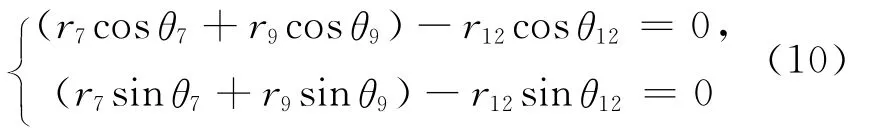
已知r7、r9及θ7、θ12（θ12＝270°），利用牛顿－辛普森法，可求出r12和θ9。即上工作辊S辊的辊心坐标已求出。

3 轧机调整关系曲线

3.1 压下调整

森吉米尔轧机的压下，是通过压下齿条驱动两个上部支撑辊组B及C的内偏心环转动来实现的，即通过图3a中向量R1的转动，从而实现上工作辊的压下及抬起。将向量R1的角度θ1作为变量，可计算出压下齿条移动量与工作辊压下量的关系曲线（图4）。

以公称辊径为例，压下齿条行程为140mm，则工作辊最大压下量为6.087mm。

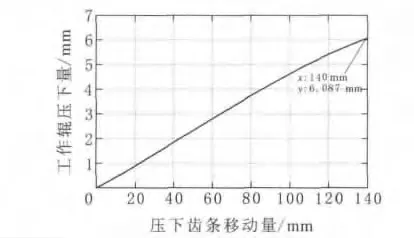
图4 压下齿条移动量与工作辊压下量关系

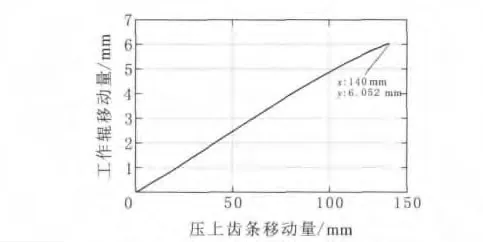
图5 凸度调节齿条移动量与工作辊凸度变化量关系

3.2 AS－U－ROLL调整

森吉米尔轧机的AS－U－ROLL调整，是通过凸度调节齿条驱动两个上部支撑辊组B及C的外偏心环转动来实现的，即通过图3a中向量R13的转动，从而实现上工作辊的凸度调整。将向量R13的角度θ13作为变量，可计算出凸度调节齿条移动量与工作辊凸度变化量的关系（图5）。以公称辊径为例，ASU－ROLL压下齿条行程为79mm，则工作辊最大弯辊量，即最大凸度变化量，为0.441mm。

3.3 压上调整

森吉米尔轧机的压上，是通过压上齿条驱动两个下部支撑辊组F及G的偏心环转动来实现的，即通过图3a中向量R1的转动，从而实现下工作辊的压上和下降。将向量R1的角度θ1作为变量，去掉向量R13，可计算出压上齿条移动量与工作辊压上量的关系（图6）。以公称辊径为例，压上齿条行程为140mm，则工作辊最大压上量为6.052mm。

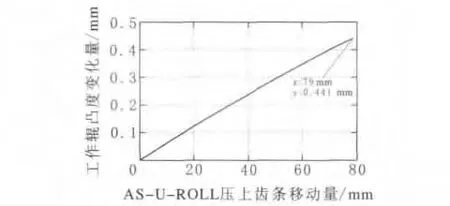
图6 压上齿条移动量与工作辊压上量的关系曲线

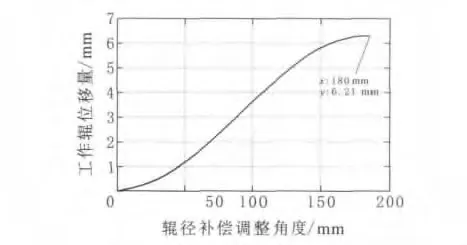
图7 辊径补偿调整角度与工作辊位移量的关系曲线

3.4 偏心调整

森吉米尔轧机的侧偏心补偿，是通过圆柱齿轮驱动两对支撑辊组A、H及D、E的偏心环转动来实现的，即通过图3a中向量R3的转动，从而实现上工作辊的压下及抬起。将向量R3的角度θ3作为变量，可计算出辊径补偿调整角度与工作辊位移量的关系（图7）。

4 结论

本文利用闭环矢量方程建立了某20辊森吉米尔轧机辊系的运动学分析模型，运用该模型对各辊辊心坐标进行求解，并对轧机各种调整结构与工作辊压下量的关系曲线进行求解，为实际生产中工艺方案的制定提供理论依据。所采用的方法简单明了，对分析类似结构的轧机具有借鉴意义。

［1］ 潘纯久.二十辊轧机及高精度冷轧钢带生产［M］.北京：冶金工业出版社，2003.

［2］ 汪朝晖，严育才，张耀兵等.20辊森吉米尔轧机轧制过程中的辊系受力分析［J］.华中科技大学学报（自然科学版），2013，41（02）：18－21.

［3］ John Gardner，机构动态仿真－使用 MATLAB和SIMULINK［M］.西安：西安交通大学出版社，2002.