克雷伯氏杆菌代谢网络的基元模式优化分析!

阚南方，张青瑞，杨晓萌，曹长青

（青岛科技大学化工学院，山东 青岛266042）

细胞内的代谢网络是一组酶反应及传输互动的过程。体内途径通量的量化是细胞生理学和代谢工程学的一个重要目标。随着计算机技术的迅速发展，凭借数学和计算机系统结合理论方法对代谢过程进行量化分析，从而提高反应效率和产物转化率，有助于改进现有的生物反应技术［1－2］。

大多数理论方法，例如代谢通量分析（MFA），都是以代谢网络中各种代谢产物的化学计量反应为基础［3］。代谢网络的反应细节与实验测得的胞外代谢产物积累速率相结合，以此为约束条件来确定通量分布。以化学计量为约束，线性规划被用来最大化目标函数，这同样在通量平衡分析（FBA）中使用［3］。这些方法已广泛应用于各种微生物系统中。近年来，代谢网络的反应细节已经被用来确定基元模式，它被定义为与胞外代谢产物相关的最小酶集合［4］，这些酶可以使该模式能够在稳定的代谢通量分布状况下朝一定方向进行。基元模式分析易估计代谢产物的最大产量，确定反应方向所固有的通量分布以及使用矩阵代数确定代谢网络的通量［5］。Xu等［6］利用基元模式分析了酿酒酵母（Saccharomyces cerevisiae）的葡萄糖厌氧发酵过程，预测出了最佳代谢路径及代谢表型，有效地指导了工程菌株酿酒酵母的构建，提高了乙醇产量。赵权宇等［7］综述了基元模式分析（elementary modes analysis，EMA）的算法和软件开发现状及其在代谢通量分解、生物过程模拟、菌株设计等方面的应用。

1，3－丙二醇（1，3－PD）作为具有优良性质的聚酯、聚醚和聚亚胺酯的单体，是一种应用前景广阔的化工原料［8］。生物柴油的生产过程中会副产10%的粗甘油，而克雷伯氏杆菌（K.pneumoniae）可将此粗甘油作为碳源和能源物质来生产高附加值的1，3－PD，既解决了粗甘油的处理问题又降低了不可再生资源的消耗，减少了环境污染。因此，微生物法生产1，3－PD越来越受到人们的重视［9］。

作者在此利用K.pneumoniae不同发酵阶段下实验测得的胞外代谢产物积累速率，以基元模式为约束条件，应用线性规划对其微氧和厌氧发酵进行优化分析，拟为菌株改造和1，3－PD生产提供理论指导。

1 克雷伯氏杆菌代谢网络模型与算法

1.1 代谢网络模型

根据文献［10］和相关的生物化学知识构建K.pneumoniae代谢甘油的代谢网络，如图1所示。

为减少不必要的基元模式，便于分析，该代谢网络未考虑胞外代谢物琥珀酸和乙醛酸循环。微氧代谢网络包括38个胞内代谢物、17个胞外代谢物、52个不同的反应，该网络主要存在于糖酵解途径（EM）、戊糖磷酸途径（PP）、完整的三羧酸（TCA）循环、氧化磷酸化途径和1，3－PD合成等代谢途径中。厌氧代谢网络包括33个胞内代谢物、16个胞外代谢物、41个不同的反应。在厌氧条件下TCA循环是不完整的［10］（包括生成酮戊二酸的氧化途径）且不包括氧化磷酸化途径。

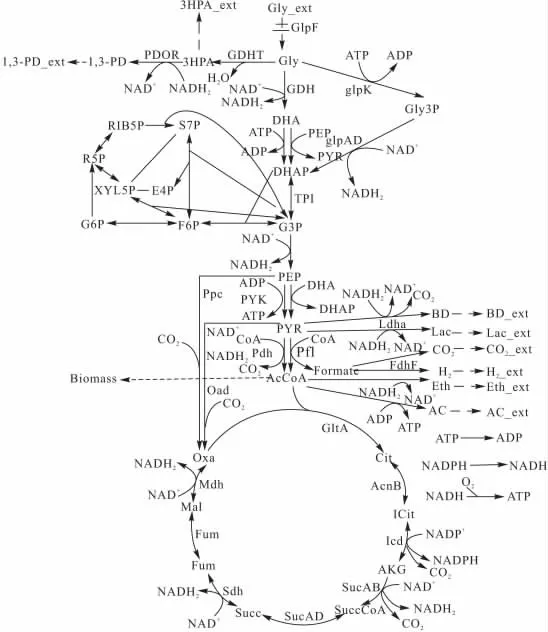
图1 克雷伯氏杆菌的代谢网络模型Fig.1 Metabolic network mode for K.pneumoniae

1.2 算法

采用Metatool 5.1软件对K.pneumoniae代谢网络进行基元模式分析，采用Matlab软件，利用线性规划求解不同发酵阶段各基元模式通量分布，具体算法步骤如下：

目标函数为：

约束条件为：

式中：Z为基元模式通量rj的线性组合；i为测量的代谢产物；j为基元模式；cj为生物量在第j个基元模式的化学计量系数；rj为第j个基元模式的通量；Sij为第i个代谢产物在第j个基元模式中的化学计量系数；vi为第i个可测代谢产物积累速率。

1.3 实验数据

K.pneumoniae代谢甘油产1，3－PD的实验数据、发酵培养基组成、发酵条件参见文献［11］。甘油、1，3－PD和乙醇的不同发酵阶段的积累速率由相邻2h测得的积累量差计算得到，如表1所示。

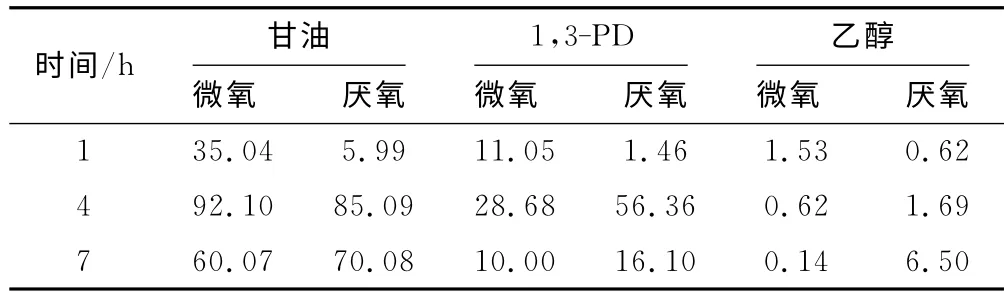
表1 各种代谢产物在不同时间点的积累速率／（mmol·L－1·h－1）Tab.1 Accumulation rates of various metabolites at different time points／（mmol·L－1·h－1）

由表1可看出，延迟期［11］（0～2h），细胞物质开始增加，菌株几乎不增加；对数期（2～6h），菌株生长提供了足够的物质基础，代谢旺盛，1，3－PD有较高的积累速率；稳定期（6～8h），营养物质不断消耗，菌株数目保持相对稳定，1，3－PD积累达到最高峰。

2 结果与讨论

利用基元模式对K.pneumoniae代谢网络进行代谢途径分析，在微氧条件下计算可得771个基元模式，在厌氧条件下计算可得97个基元模式。

以生物量最大化为目标函数，甘油消耗速率标准化为1mol·L－1·h－1，在微氧和厌氧条件下以甘油、1，3－PD、乙醇为决定变量，应用线性规划计算K.pneumoniae在微氧和厌氧条件下不同发酵阶段各基元模式合成生物量和1，3－PD的通量值见图2。在微氧条件下因从第182个基元模式后生物量和1，3－PD合成的通量值几乎为零，故在图2a～f中省略。

2.1 不同发酵阶段最优模式分析

2.1.1 微氧条件下最优模式分析

本实验的最优模式为各发酵阶段生物量合成的积累速率最大的基元模式。由图2a～c可见，在微氧条件下，不同发酵阶段的最优模式是相同的，即模式124、146、178、182。这4个最优模式途径都包含EM途径、PP途径、TCA循环、转氢酶途径、氧化磷酸化途径和1，3－PD合成途径。它们的主要区别在于：（1）甘油（GLY）转化为磷酸二羟基丙酮（DHAP）的途径不同。在模式124、178中，GLY经甘油脱氢酶（GDH）、二羟丙酮激酶（DHAK）催化生成DHAP；模式146、182启动了GLP系统，即GLY经甘油激酶（glpK）、3－磷酸甘油醛脱氢酶（glpAD）催化生成DHAP；（2）磷酸烯醇式丙酮酸（PEP）生成丙酮酸（PYR）的途径不同。在模式124、146中，PEP经丙酮酸激酶（PYK）催化生成PYR；在模式178、182中，1，3－二羟基丙酮（DHA）经DHAK催化和PEP参与反应生成PYR。虽然具体反应路径有些不同，但节点后反应通量相同，故增加了其最优模式途径。

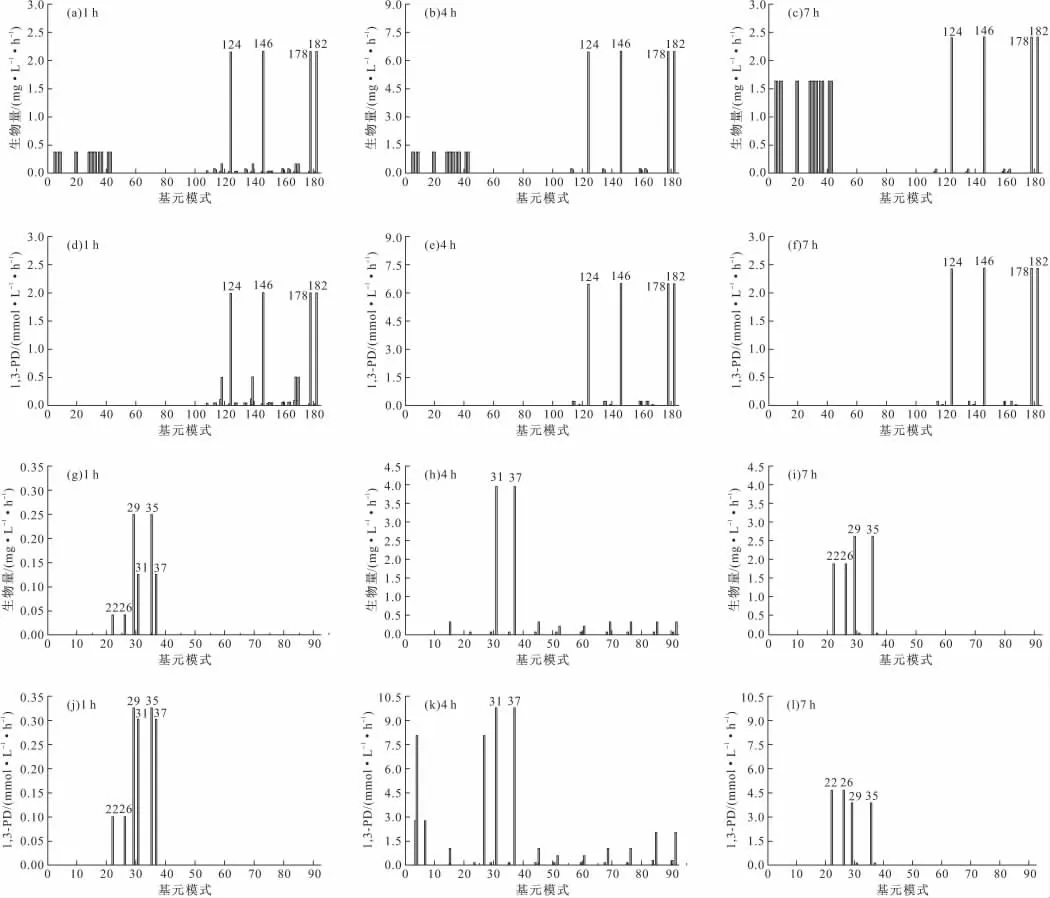
图2 不同时间点各基元模式合成生物量和1，3－PD的通量值Fig.2 The biomass and 1，3－PD fluxes of elementary modes at different time points

在不同发酵时间点（1h、4h、7h），每个最优模式的生物量积累速率分别为2.16mg·L－1·h－1、7.30 mg·L－1·h－1、2.60mg·L－1·h－1，4个最优模式的生物量积累速率之和分别占各发酵阶段总生物量的56%、67%、29%。由图2a～c还可以看出，除了最优模式，各发酵阶段下剩下的生物量合成几乎平均分配在5、6、8、9、19、20、28、29、30、31、32、33、35、37、41、43次优模式中，除了含有EM途径、PP途径和TCA循环外，还增加了PEP生成草酸乙酸（Oxa）的回补路径。次优模式在不同发酵阶段的生物量积累速率分别为0.38mg·L－1·h－1、0.912mg·L－1·h－1、1.617 mg·L－1·h－1，其生物量积累速率之和分别占各发酵阶段总生物量的42.4%、43.8%、43.9%。由此可以看出，微氧条件下，延迟期和对数期对生物量合成有利的途径主要集中在最优模式。而在稳定期，次优模式对生物量合成的影响逐渐增大。另外，对于生物量的合成，延迟期启动的基元模式较多，但贡献量主要集中在最优和次优模式中，其余模式贡献量相对较少，对数期和稳定期启动的基元模式相对较少，但在对数期最优模式对生物量的贡献尤为突出。

由图2d～f可以看出，在不同发酵时间点（1h、4h、7h），每个最优模式的1，3－PD积累速率分别为2.0mmol·L－1·h－1、6.8mmol·L－1·h－1、2.4mmol·L－1·h－1。在对数期和稳定期，1，3－PD合成几乎都由最优模式提供。在延迟期，基元模式启动较多，此发酵阶段71%的1，3－PD合成量由最优模式提供，剩下的1，3－PD合成量几乎平均分配在模式118、139、168、170中，与最优模式相比，未启动氧化磷酸化途径，增加了乙酰辅酶A（AcCoA）消耗NADH2生成副产物乙酸的反应，其1，3－PD积累速率均为0.464 mmol·L－1·h－1，贡献了此发酵阶段1，3－PD总合成量的27%。总之，在微氧条件下，对数期的最优模式对生物量和1，3－PD合成贡献较大。

2.1.2 厌氧条件下最优模式分析

由图2g～i可见，在厌氧条件下，第1h、7h，模式29、35为最优模式；第4h，模式31、37为最优模式。与微氧相比，该4个基元模式主要途径不包含氧化磷酸化途径和GLP系统。它们的主要区别在于：（1）PEP转化为PYR的途径不同。在模式29、35中，PEP经PYK催化生成PYR；在模式31、37中，DHA经DHAK催化和PEP参与反应生成PYR；（2）AcCoA生成的副产物不同。在模式29、35中，AcCoA消耗NADH2生成副产物乙醇（Eth）；在模式31、37中，Ac－CoA消耗ATP生成副产物乙酸（AC）。

在第1h、7h，最优模式29、35的生物量积累速率分别为0.252mg·L－1·h－1、2.60mg·L－1·h－1，其积累速率之和分别占各发酵阶段总生物量的61%、59%；在第4h，最优模式31、37生物量积累速率为3.9mg·L－1·h－1，占该发酵阶段总生物量的80.2%。由图2g～i还可以看出，除了最优模式，模式22、26在延迟期和稳定期中也在运行，除了含有EM途径、PP途径和TCA循环外，在PYR节点处经乳酸脱氢酶（Ldha）催化消耗NADH2生成了副产物乳酸，其生物量积累速率分别为0.0402mg·L－1·h－1、1.8 mg·L－1·h－1，其积累速率之和分别占各发酵阶段总生物量的9.7%、41%。此外，模式31、37在对数期为最优模式，但在延迟期对生物量的贡献也较显著，其生物量积累速率为0.121mg·L－1·h－1，其积累速率之和占该发酵阶段总生物量的29.3%。由此可以看出，厌氧条件下，延迟期和稳定期基元模式启动较少，对生物量贡献较为集中；而在对数期基元模式启动较多，最优模式31、37对生物量贡献尤为突出。

由图2j～l可以看出，在第1h、7h，最优模式29、35的1，3－PD积累速率分别为0.322mmol·L－1·h－1、3.8mmol·L－1·h－1，其积累速率之和分别占各发酵阶段总合成量的44.3%、42.5%；在第4h，最优模式31、37的1，3－PD积累速率为9.7mmol·L－1·h－1，占该发酵阶段总生物量的40.4%。由图2j～l可以看出，模式22、26在延迟期和稳定期的1，3－PD积累速率分别为0.101mmol·L－1·h－1、4.57mmol·L－1·h－1，贡献了各发酵阶段1，3－PD总合成量的13.9%、57.3%。模式31、37在延迟期的1，3－PD积累速率为0.304mmol·L－1·h－1，贡献了此发酵阶段总1，3－PD合成量的41.8%。而对数期基元模式启动较多，除了最优模式外，其余模式贡献了此发酵阶段1，3－PD合成量的59.6%。总之，在厌氧条件下，对数期的最优模式对生物量和1，3－PD合成贡献较大。

综上所述，无论微氧和厌氧条件，生物量和1，3－PD合成都主要集中在对数期，尤其在微氧条件下，其合成量在对数期明显高于延迟期和稳定期。

2.2 不同发酵阶段NADH2、ATP代谢分析

K.pneumoniae代谢网络中，EM途径和转氢酶途径提供还原当量NADH2，1，3－PD合成时消耗NADH2。其中，DHA在DHAK催化下生成DHAP时消耗ATP，PEP在PYK催化下生成PYR时提供ATP。在微氧条件下，K.pneumoniae代谢网络启动了GLP调控系统和氧化磷酸化途径。其中，GLP调控系统提供ATP和消耗NADH2，在氧化磷酸化途径中氧气作为电子受体，NADH2可经过呼吸链将电子传递给氧气，同时偶联着NAD＋和ATP的形成。此外，PYR在丙酮酸脱氢酶（Pdh）催化下生成AcCoA时提供NADH2。而在厌氧条件下，通过生成乙酸等副产物消耗NADH2、合成目的产物1，3－PD来调节NAD＋／NADH2的平衡。

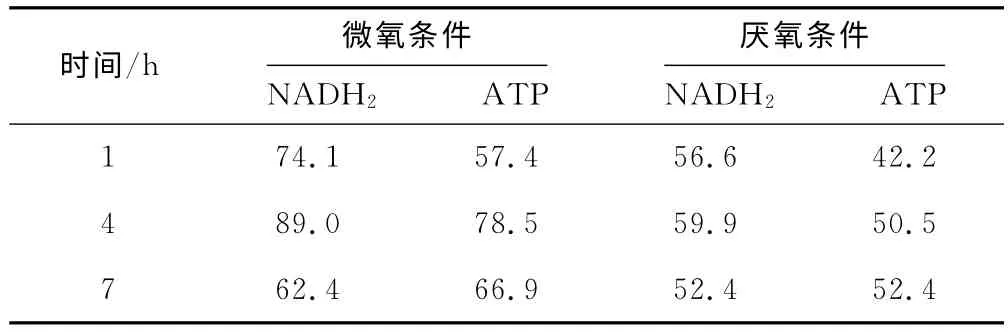
表2 在微氧和厌氧条件下不同时间点最优基元模式的NADH2、ATP百分比／%Tab.2 The percentage of NADH2，ATP from the optimal elementary modes at different time points under micro－aerobic and anaerobic conditions／%

由表2可见，无论微氧和厌氧条件，各发酵阶段最优模式对NADH2、ATP的贡献均较大。其中微氧条件下的对数期尤为突出。微氧条件下，最优模式在对数期贡献了此发酵阶段的89.0%的NADH2和78.5%的ATP；厌氧条件下，对数期基元模式启动较多，最优模式31、37集中贡献了59.9%的NADH2和50.5%的ATP。在厌氧条件下，1，3－PD合成是为细胞生长维持NAD＋／NADH2平衡不可或缺的途径［9］，存在转氢酶途径，无氧化磷酸化途径。模式29、35经生成乙醇消耗NADH2，模式31、37经生成乙酸提供ATP。在微氧条件下，最优模式除满足目的产物1，3－PD合成对NADH2的需要外，还可通过氧化磷酸化途径和转氢酶途径调节NADH2，同时产生足够的ATP。因此，和厌氧相比，K.pneumoniae代谢在微氧条件下启动了氧化磷酸化途径，无副产物产生，更利于生物量和1，3－PD的合成。

综上所述，如果想要最大化地繁殖菌株，以利于目的产物1，3－PD的合成，除优化发酵过程外，应改进现有的生物反应技术，应用基因敲除或过表达操作手段切断竞争路径、增强生物量和1，3－PD合成路径通量，控制代谢路径使之向最优基元模式方向进行，减少不必要的路径造成的还原力、能量和碳源的消耗，通过调节代谢网络中酶活性或构建NADH2再生系统等手段维持NAD＋／NADH2和ATP／ADP平衡，实现生物量和1，3－PD合成最大化。

3 结论

从基元通量模式（elementary flux mode，EFM）角度分析，以生物量最大化为目标函数，应用线性规划量化K.pneumoniae代谢网络，发现：在微氧条件下，不同发酵阶段生物量合成的最优模式是相同的，即模式124、146、178、182；在厌氧条件下，延迟期和稳定期的最优模式为模式29、35，对数期为模式31、37。同时，各最优模式对1，3－PD合成贡献也较大；代谢过程中，氧化磷酸化途径对维持NAD＋／NADH2和ATP／ADP平衡起着重要作用。表明，可以用基元模式分析结合线性规划来量化K.pneumoniae生产1，3－PD的代谢网络。

［1］Forster J，Gombert A K，Nielsen J.A functional genomics approach using metabolomics and in silico pathway analysis［J］.Biotechnology and Bioengineering，2002，79（7）：703－712.

［2］Klamt S，Stelling J.Two approaches for metabolic pathway analysis［J］.Trends in Biotechnology，2003，21（2）：64－69.

［3］Gayen K，Venkatesh K V.Analysis of optimal phenotypic space using elementary modes as applied to Corynebacterium glutamicum［J］.BMC Bioinformatics，2006，7：445.

［4］杨建刚.基于基元模式分析产琥珀酸大肠杆菌的构建［D］.天津：天津大学，2012.

［5］Poolman M G，Venkatesh K V，Pidcosk M K，et al.A method for the determination of flux in elementary modes，and its application to Lactobacillus rhamnosus［J］.Biotechnology and Bioengineering，2004，88（5）：601－612.

［6］Xu X J，Cao L M，Chen X.Elementary flux mode analysis for optimized ethanol yield in anaerobic fermentation of glucose with Saccharomyces cerevisiae［J］.Chinese Journal of Chemical Engineering，2008，16（1）：135－143.

［7］赵权宇，于水燕，史吉平.基元模式分析在生物网络和途径分析中的应用［J］.生物工程学报，2013，（6）：701－715.

［8］张宏蕊，金平，刘树臣.发酵1，3－丙二醇的关键酶研究进展［J］.化学与生物工程，2011，28（3）：1－4.

［9］苗茂栋，吴敏，邵千飞，等.利用克雷伯肺炎杆菌限制性底物发酵生产1，3－丙二醇［J］.中国生物工程杂志，2008，28（10）：49－54.

［10］张青瑞.甘油生物转化为1，3－丙二醇过程的代谢通量分析与动态模拟［D］.大连：大连理工大学，2008.

［11］王元好.微氧发酵制备1，3－丙二醇及其代谢流量分析［D］.大连：大连理工大学，2011.