直驱式永磁同步风电系统控制算法研究

侯文宝，周 鑫，庞晴晴

(1.江苏建筑职业技术学院，江苏徐州221116;2.中石化徐州管道技术作业公司，江苏徐州221008;3.中国矿业大学，江苏徐州221008)

0 引 言

永磁同步风电系统的优势可概括为无励磁装置、质量轻、效率高、系统可靠性好等。与其他风力发电系统相比，永磁发电机和风轮机之间无需减速箱，可以实现直接耦合，大大降低了发电机的维护成本，同时有利于改善系统噪声。因此去掉齿轮箱的直驱式风电系统成为目前的发展趋势［1－2］。

在额定风速下运行时，变速恒频风力发电系统相较于恒速恒频风力发电系统，可以获取更多的能量［3］。为了达到这个目的，需要发展先进的最大功率跟踪控制技术，目前常用的有［4］功率信号反馈法和爬山搜索法。但在使用功率信号反馈法时，需要模拟仿真得到最大功率曲线，实现起来相对麻烦［5］;爬山搜索法需要步长的设置，定步长算法中，步长设置过大或过小都有其不好的一面，而变步长算法增加了计算量。永磁同步电机的控制方法最常用的是矢量控制方式，使用最多的是［6］零d 轴电流控制、最大转矩电流比控制、单位功率因数控制和恒定子磁链控制。零d 轴电流控制以及最大转矩电流比控制，在低速时能保持较高的效率，但是高速时无功功率增加，功率因数降低。单位功率因数控制方式中电枢电流不是线性关系，控制比较麻烦。

本文选用叶尖速比控制法实现最大风能跟踪，基于恒定子磁链控制实现永磁同步发电机的高性能控制。该控制方式直接明确，在变风速时也能保持风能最佳利用率，功率因数高，适用于大功率系统中。MATLAB/Simulink 仿真及基于dSPACE 的变速恒频风力发电实验平台实验，验证了所述方法的正确性与可行性。

1 永磁同步电机的数学模型

为了简化永磁同步发电机的基本电磁关系，通常忽略涡流和磁滞损耗及铁心磁饱和影响，并假设永磁材料电导率为零，定子三相绕组对称安放，定子中感应电动势为标准正弦波，转子无阻尼绕组等［8－9］。

图1 为三相永磁同步发电机的结构分布图。图中定子三相绕组的轴线呈对称分布，在空间中按逆时针顺序排列，每相绕组之间互差120°电角度。永磁同步电机转子上只安放永磁体，不存在绕组线圈，由永磁体提供磁链。对应于某一特定电机，永磁体磁链的最大值为一定值ψf，并正弦分布于定转子气隙中。在外力作用下，转子以角速度ωe旋转时，由于定转子之间的相互运动，定子绕组将切割转子磁链，从而在定子绕组中产生三相电压。当运动方向为逆时针时，定子中三相电压为正序电压。

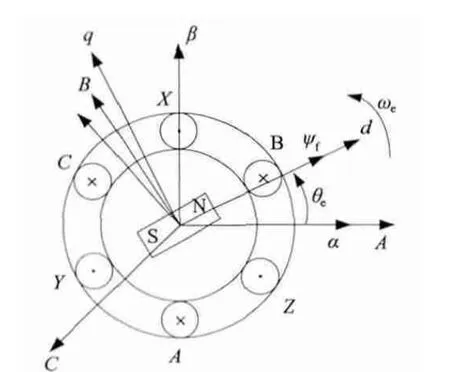
图1 永磁同步发电机结构简图

图1 中，θe为ψf与A 相绕组间的夹角;θ0为电机的初始相位角，有θe=ωet+θ0。

永磁同步电机在d、q 坐标系下的数学模型［10］如下:

定子磁链方程:

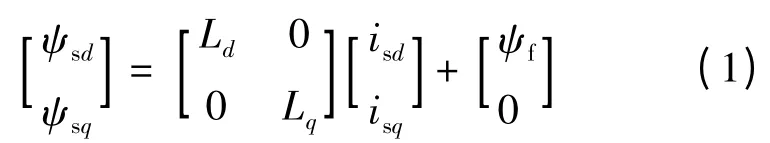
定子电压方程:

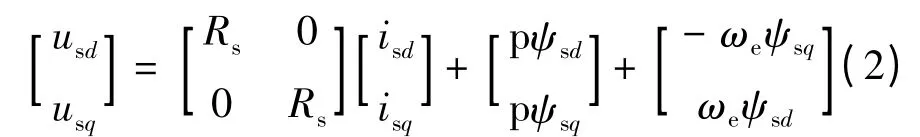
由式(1)、式(2)得:

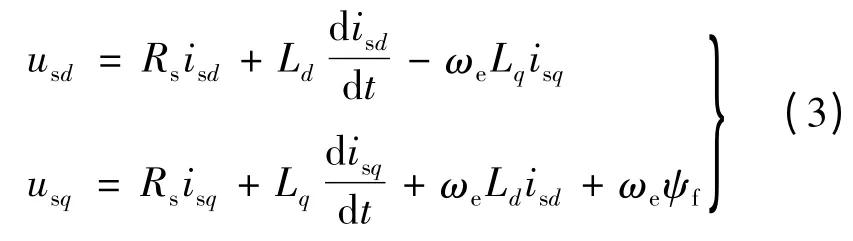
式中:usd、usq为交直轴等效电压;ωe为转子旋转电角度;Rs为永磁同步电机定子每相电阻。

电机的电磁转矩表达式:

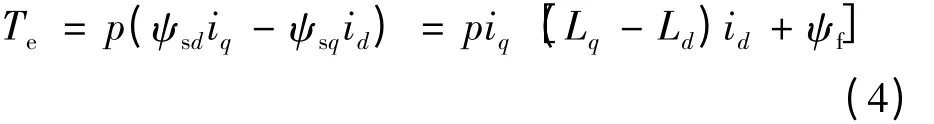
式中:p 是发电机极对数。

2 风力机最大功率跟踪的叶尖速比控制法

在风力发电机系统中，风力机的输入机械转矩特性曲线是实现风力机的最大功率跟踪的基础。因此首先需要获得风机的输出机械功率和转速的特性曲线。需要取多组风速，分别计算出每组风速下风机的输出机械功率。先选取某一风速，调节风机转速，计算不同叶尖速比分别对应的功率，绘制该风速下的功率和风机转速得关系曲线，找到最大功率点时的风机转速，此时对应的叶尖速比即为最佳叶尖速比λ*。为了得到风机功率和转速的特性曲线，需要多组不同风速下的功率转速关系。改变风速，按上述同样方法，得到不同风速下的功率－转速特性曲线，如图2 所示。连接不同风速对应的最大功率点得到的曲线即为最佳功率曲线Popt［11－12］。对于某一特定的风速，最大功率点对应风机的某一特定转速。

图2 风机转速－功率关系曲线

图3 是获得最佳叶尖速比的控制原理图。引入负反馈，改变发电机转速以调节系统叶尖速比λ，逐渐接近并最终等于λ*，从而获得最佳叶尖速比。由于风速具有随机性和不确定性的特点，难以保证风速测量的精度，同时实际执行的难度和系统的成本也将大大增加［13］。

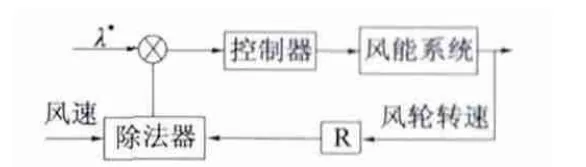
图3 最佳叶尖速比法框图

机组的最大功率跟踪过程如图2 所示。描述如下:假设某一时刻风速为v3，根据对应于此风速下的功率－转速曲线，此时风力机获得的功率等于发电机获得的功率P1，系统工作于E 点，以转速n3稳定运行。由于风速的不确定性，在某一时刻假设风速突然增大至v2，根据最佳功率曲线，风力机在A 点获得最大功率，由于发电机的机械惯性和调节过程的滞后，发电机转速不能跳变，仍然保持在E 点，此时电功率P1小于风力机输出的机械功率P2，因此使转速增大。风力机和发电机分别沿图2 中曲线A→B 和E→B 增速，在此过程中，发电机和风力机之间的功率差值逐渐缩减，直到B 点功率再次达到平衡，此时不再加速，机组以转速n2稳定运行。B 点为风力机功率－转速曲线和最佳功率曲线的交点。若初始风速为v1，某一时刻减小到v2，v2对应的最佳功率点为D 点，同样道理，风力机的工作点由C 点跳变到D 点，此时发电机工作状态仍保持在C 点，由于电功率大于风力机的机械功率，转速降低，曲线D→B 和C→B 分别为风力机和发电机转速变化趋势，到达功率平衡点B 点时，转速停止下降，机组以转速n2稳定运行。实现不同风速的最大功率跟踪。

本文风力机的仿真参数:空气密度1.225 kg/m3，风力机半径为34 m，额定风速为13 m/s，风力机在静态时，桨矩角β 为0。风速模型如图4 所示，风速从0 开始增大，逐渐增大并稳定在11 m/s，直至0.8 s，在0.8 s 时，风速开始下降，并稳定在7 m/s，1.6s 时风速再次上升并稳定在额定风速13 m/s，直到仿真结束。通过调节风力机转速与主导变速风速之间的比例系数，使其保持在最佳的比例系数。风力机处于最佳功率捕获系数情况下，变速风力机可实现最佳的输出转矩和功率。风力机的输出最佳转矩曲线和最佳功率曲线如图5、图6 所示，图7 为叶尖速比λ 和风能利用系数Cp波形。

从图5 可以看出，输出电磁转矩随输入机械转矩的变化而变化;从图6 可以看出，输出电磁功率跟随输入机械功率的变化而变化;从图7 可以得到风能利用系数Cp为0.412，对应的最佳叶尖速比λ =6.02。仿真数据及仿真波形表明，当风力机以最佳叶尖速比运行时，即风机转速与风速之间保持最佳比例系数，风力机可以实现风能最大功率的实时捕获。

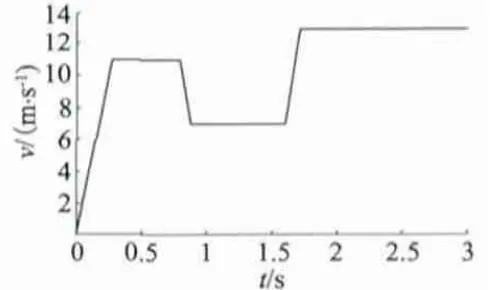
图4 风速模型

图5 输入机械转矩和输出电磁转矩波形

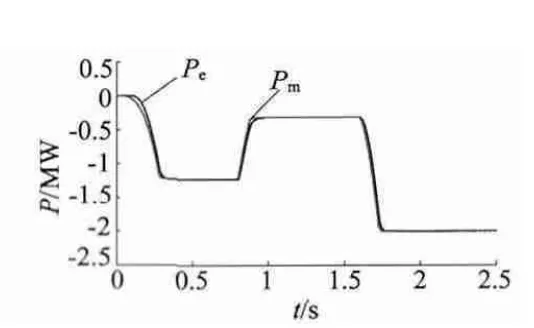
图6 输入机械功率和输出电磁功率

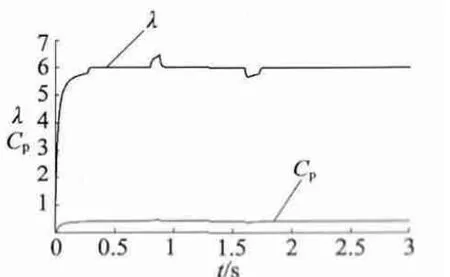
图7 叶尖速比λ 和风能利用系数Cp 波形

3 永磁同步电机的控制策略

恒定子磁链的控制思想是通过控制电机的交、直轴电流，使电机的全磁通在定子绕组中产生的定子磁链|ψS|恒为固定值，取|ψS| = |ψf|，其矢量图如图8 所示。

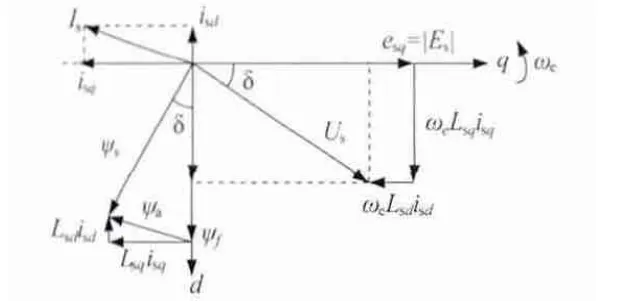
图8 采用恒定子磁链控制时永磁发电机相量图

恒定子磁链控制保持定子磁链为恒值，使得发电机在转速一定的情况下，其端电压不跟随负载电流Is的上升而变大。由此得到定子磁链方程:

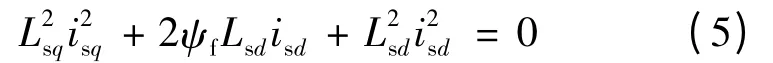
isd和isq间的关系:

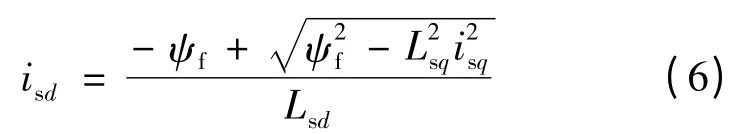
可推得电流给定:

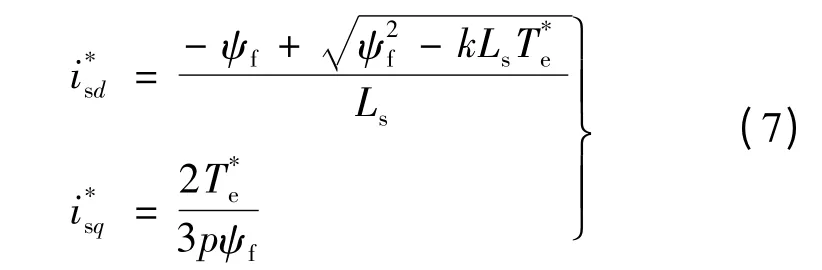
发电机定子电流d、q 轴分量受控制电压与耦合电压的双重影响，解耦后，经PI 调节器可得:

4 仿真结果及分析

为验证上述理论分析和系统设计原理，在MATLAB 进行仿真验证，搭建直驱型风力发电机侧仿真模型。采用最佳叶尖速比控制算法实现风力机最大风能追踪，获得的最大功率控制器是采用电流内环速度外环的控制算法来实现，机侧变流器的控制框图，如图9 所示。永磁同步发电机参数:定子额定电压为660 V，定子额定电流为1 750 A，额定转速22.5 r/min，额定频率11.25 Hz，额定功率为2 MW，定子绕组等效电阻Rs=0.006 65 Ω，Ld=1.3 mH，Lq=2.3 mH，p=30，ψf=7.8 Wb。图10 为实际转速和目标转速的波形图，图11 为定子电流d 轴分量、q 轴分量，图12 为发电机侧输出三相电流波形。

图10 为发电机转速和最优化的目标转速，由图10 可以看出，发电机转速实现了对最优化的目标转速的稳定跟踪;图11 为发电机定子侧isq、isd的给定和反馈波形，isq、isd的给定和反馈值由给定的电磁转矩根据恒定子磁链控制计算得到，可以看出，电流的跟随性良好;图12 为发电机侧输出电流波形，从图12 中可以看出三相电流对称，电流的正弦度良好，其频率和幅值随着风速的变化而变化。仿真结果证明了MPPT 控制方法是行之有效的，可以实现风能的最大功率跟踪，体现了变速风力发电系统的诸多优势:工作稳定且易于实现最大功率的捕捉。由仿真结果看出电流畸变率＜5%，系统具有良好的动稳态性能，符合实际要求。

5 基于dSPACE 实验平台的直驱式永磁同步发电机研究

由于仿真模型及其参数的非真实性和控制算法的非实时性，可能造成仿真结果不完全符合模拟系统的试验。为了验证该方法在实际中的可行性，本文基于永磁直驱发电机运行原理的理论分析，构建了VSCF 永磁直驱发电机控制系统的dSPACE 实验平台。鉴于实验条件所限，没有多级低速电机，故采用普通永磁电机作为验证控制策略的对象。

本文的永磁直驱发电机控制实验平台建立在DS1103 单板处理器上的功率为30 kW 的交－直－交传动实验平台，该平台包括了全控器件组成的机侧变流桥、网侧变流桥。桥路由1 200 V、150 A 的IPM 组成，具备完整的电气主回路控制和保护元件，以及完备的功率器件桥的驱动触发、吸收和保护回路。功率器件桥的触发控制PWM 脉冲为光纤接口。另外，平台还设有必需的电压和电流传感器。另外系统还提供交－ 直－ 交传动实验平台和dSPACE 仿真系统之间的接口电路。图13 为系统结构框图，图14 为发电机侧变流器板。

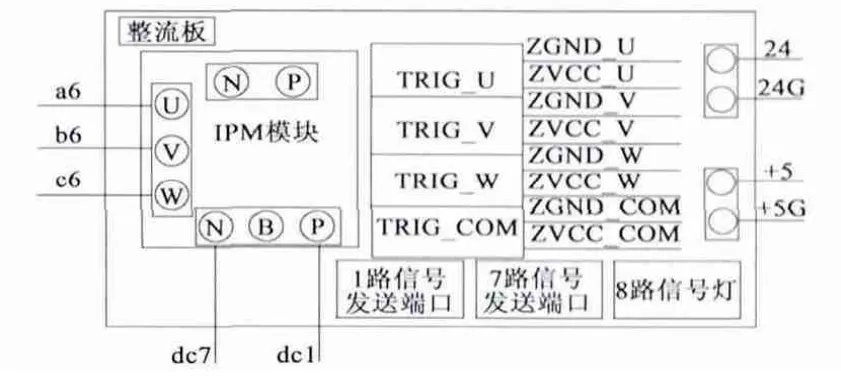
图14 发电机侧变流器板

根据基于永磁直驱式风电系统发电机侧的控制算法的研究，利用基于dSPACE 的硬件实验系统得到的实验结果如下。实验中系统初始给定转速为300 r/min，电机能实现跟踪给定并保持稳定运行。后将给定转速增加到500 r/min。图15 依次对应系统运行过程中发电机转速响应曲线、转矩响应曲线、转子位置响应曲线以及定子三相电流波形。

图15 永磁直驱式风电系统发电机侧的控制试验形

通过图15 的实验波形可以证明，基于dSPACE实验平台建立的永磁直驱式风电系统发电机侧的控制系统的实验效果与MATLAB 仿真结果一致，由此可见系统能够较好地跟踪实际转速，在给定转速突变的情况下仍能做到快速跟踪实际值。系统起动平稳，超调小，调速性能较理想。实验结果验证了本方法具有较好的静、动态性能。

6 结 语

本文阐述了风力发电系统中最佳叶尖速比实现最大功率跟踪的原理，对该理论进行了仿真验证。并基于永磁同步电机在两相旋转坐标系中的数学模型，分析了恒定子磁链控制方法实现永磁同步电机的矢量控制。搭建了基于MATLAB 的整个风电系统的仿真模型，并进行了仿真结果的分析，验证了所提出的控制方法的有效性。最后构建基于dSPACE实验平台的永磁直驱式风电系统，进一步验证了实际可行性。

［1］ 金玉洁，毛承雄，王丹，等. 直驱式风力发电系统的应用分析［J］.能源工程，2006(3):29－33.

［2］ 李建林，周谦，刘剑，等.直驱式变速恒频风力发电系统变流器拓扑结构对比分析［J］.电源技术及应用，2007(6):12－15.

［3］ 曹淑军. 变速恒频风力发电系统最大风能追踪控制的研究［D］.天津:河北工业大学，2010:2－4.

［4］ 王星华.变速恒频同步直驱风力发电机控制系统的研究［D］.上海:上海交通大学，2007:5－7.

［5］ 刘建坤.风力发电系统的MPPY 方法研究［J］.企业技术开发，2011，30(14):58.

［6］ 李建华，胡书举，孔德国，等.全功率变流器永磁直驱风电系统低电压穿越特性研究［J］.电力系统自动化，2008，32(19):92－95.

［7］ 张雷，付勋波.不同控制目标下的永磁同步风力发电机控制策略分析［J］.大功率变流技术，2009(1):31－34.

［8］ 吴政球，干磊.风力发电最大风能追踪综述［J］.电力系统及其自动化学报，2009，21(4):88－93.

［9］ 瞿兴鸿.直驱永磁同步风力发电控制系统的研究与设计［D］.重庆:重庆大学，2008.

［10］ 王涛.永磁同步电机矢量控制系统建模与仿真［J］.河北大学学报，2011(11):648－652.

［11］ 王志新，张华强. 风力发电技术与功率控制策略研究［J］. 自动化仪表，2008(11):1－6.

［12］ 刘其辉，贺益康，赵仁德.变速恒频风力发电系统最大风能追踪控制［J］.电力系统及其自动化，2003(10):62－67.

［13］ 闫永勤，乔明，林飞，等. 变速恒频风力发电系统最大风能跟踪控制的研究［J］.电气技术，2006(11):14－17.

［14］ 贾要勤，曹秉刚，杨仲庆.风力机模拟平台的MPPT 快速响应控制方法［J］.太阳能学报，2004，25(3):364－370.

［15］ Jia Yaoqin，Yang Zhongqing，Cao Binggang. A new maximum power point tracking control scheme for wind generation［C］//Proceedings of International Conference on Power System Technology.IEEE，2002，1(10):144－148.