同性极感应子发电机空间矢量法计算三相短路电流
任章鳌,单周平
(湖南省电力公司科学研究院,湖南长沙410007)
0 引 言
同性极式感应子电机(以下简称HIA)是一种特殊的凸极同步发电机,在19 世纪后半期被发明,主要工业应用在金属的冶炼,包括由电机产生的高频涡流来融化和锻造金属。但是之后由于其应用的局限性,理论一直都没太大进展。后来在它基础上发明了异性极感应子发电机。经过研究表明,异性极感应子电机在磁路的利用率方面比HIA 高[1]。文献[2]对这两种型式的电机性能做过比较,结果表明异性极式比同性极式笨重而且损耗高、储能密度低。直到最近同性极感应子发电机才逐渐应用于航天和船舶的备用电源上。在储能技术高速发展的当今世界,感应子发电机的无刷励磁和结构简单可靠的优点,使得其非常适用于高速、高储能密度和高可靠性的场合[3-7],目前同性极感应子发电机的研究和应用又快速蓬勃地发展起来。
由于同性极感应子电机经常运行在瞬态这一特殊工况下,所以其瞬态特性的分析就显得尤为重要。国外Erdelyi Edward A 教授等对感应子电机做了很多研究,其成果都为感应子电机的瞬态特性分析提供依据[8-12]。但是选取合适的坐标参考系和研究方法来分析感应子电机的瞬态特性仍有待研究。虽然双反应理论也可以适用于该电机的分析,但是同性极感应子电机没有通常实际物理空间意义的d、q轴,传统的凸极同步电机在瞬态分析中常用的d、q变换和叠加原理不能直接用于感应子电机。由于同性极感应子电机左右空间气隙磁场错位180°电角度,空间相对不对称,只有空间合成总的气隙磁场在对称的情况下才能适用双反应理论[13],这样也使得电机的瞬态分析在d、q 坐标系下尤为复杂。本文直接采用三相电机a、b、c 绕组变量的空间矢量法来计算同性极感应电机在考虑各绕组电阻情况下的三相短路电流,使电机的瞬态特性分析更为简便。
1 HIA 结构和磁场分布
图1 和图2 是18/16 极HIA 的径、轴向剖面结构图和转子实物图。
由图1 和图2 看出,励磁绕组产生的磁场是沿着转子轴向、双边气隙和定子轴向闭合的,HIA 单边铁心下气隙磁场的极性相同,经过转子的磁通方向一定而不交变,磁场与定子左右两边绕组交链耦合;HIA 利用带齿槽的转子的齿部和槽部磁导的不同(齿上气隙磁通密度较高,槽高处磁通密度较低),使定子电枢绕组的磁链随着转子旋转而周期性脉动,从而在定子绕组中产生感应电动势的交流发电机。从物理本质上它属于同步电机。
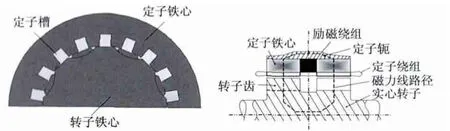
图1 18/16 极HIA 的剖面结构图

图2 HIA 转子实物图
转子可以用实心钢件锻造而成,转子上没有绕组,只是表面均匀开槽,转速可以很高,发电机的储能密度高,特别适用于高速储能系统;圆环形励磁绕组圆周方向嵌在HIA 定子中部的槽内,不占定子内腔空间,有效材料利用率高。
当励磁绕组通有励磁电流时,图3 和4 分别显示了HIA 轴向静磁场分布和空间磁力线的分布。从图4 中可以看出HIA 齿部磁力线密度比槽部大。
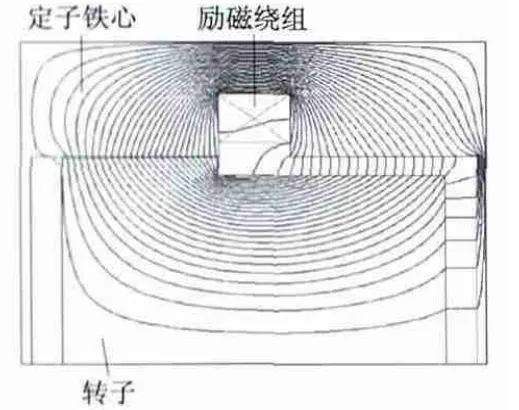
图3 HIA 轴向静磁场分布

图4 HIA 磁力线分布图
2 HIA 三相短路的瞬变电抗和等效电路
将HIA 定子三相绕组都看成集中绕组,并满足以下假设:(1)磁动势MMF 和磁通密度在气隙上呈正弦分布;(2)忽略电机端部效应;(3)忽略铁心饱和效应。
根据电磁感应和基尔霍夫定律可以得到定、转子绕组在各自坐标系下电压的空间矢量方程:

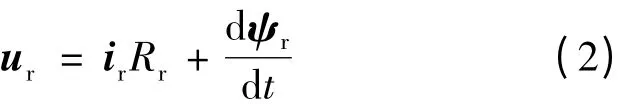
为了将定子、转子电压矢量方程统一到一个坐标系下,在转子坐标系下表示定子各变量。用isr表示定子电流在转子坐标系下的空间矢量is:

式(1)可简化:

式(4)是定子电压矢量在转子参考系下的微分方程。
应用空间矢量法计算三相HIA 的瞬态电抗,它满足任何旋转电机瞬态分析的一般定律,这里首先列写HIA 时域的微分方程,接着计算其三相对称短路时的瞬态电抗并建立等效电路模型,得到定子和励磁电流的时域解析解。在对感应子电机进行瞬态分析前作出如下假定:
(1)HIA 短路前为空载运行,Is=0,Is为稳态定子电流矢量;
(2)HIA 只有两套绕组,一套位于定子齿内并贯穿两部分定子的定子绕组,一套位于定子上的励磁绕组;
(3)忽略瞬态过程中的阻尼影响;
(4)忽略定子和励磁电阻;
(5)磁路任何部分铁心的磁阻率为0;
(6)忽略涡流效应影响;
(7)不考虑高次谐波影响;
(8)瞬态过程中HIA 的转速ωr恒定。
HIA 三相短路时,由磁链守恒可以得到转子和定子磁链方程:
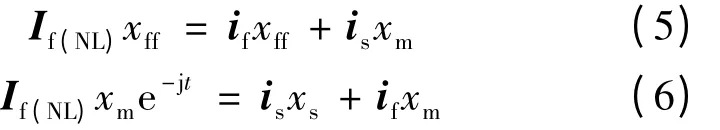
由式(5)和式(6)可以得到:
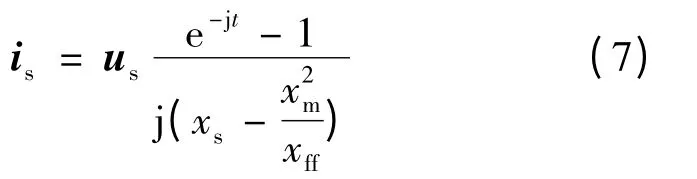
式(7)的分母就是HIA 从空载运行到三相短路的瞬态电抗,可以记为:

可以看出,它和传统同步电机的直轴瞬态电抗相似。式(8)中定子同步电抗xs可以表示为定子漏电抗和主电抗之和,即:xs=xls+xas,转子同步电抗xff也可以表示为转子漏电抗和主电抗之和,xff=xlf+xf。
因此式(8)可简化成如下的形式:

HIA 的瞬态电抗表达式通过以上的变形可以得到瞬变电抗的等效电路,如图5 所示。
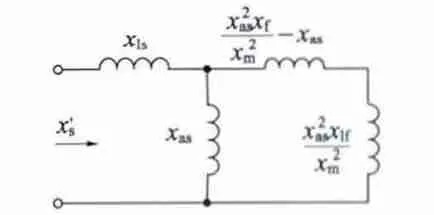
图5 HIA 三相短路时的瞬间电抗的等效电路
3 考虑各绕组电阻情况下的定、转子短路电流计算
考虑绕组电阻后,定子电压和磁链的微分方程:
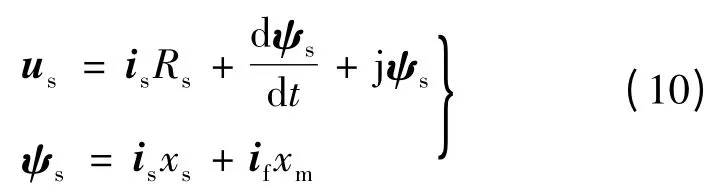
转子电压和磁链的微分方程:

定、转子在Laplace 域的电压微分方程由Laplace 变换可得:
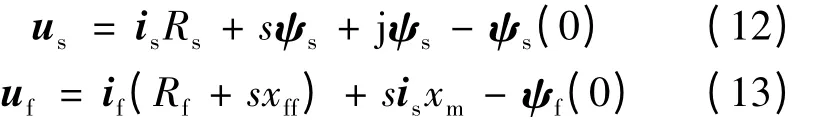
将式(13)代入式(10)可得定子在转子坐标系下的磁链:
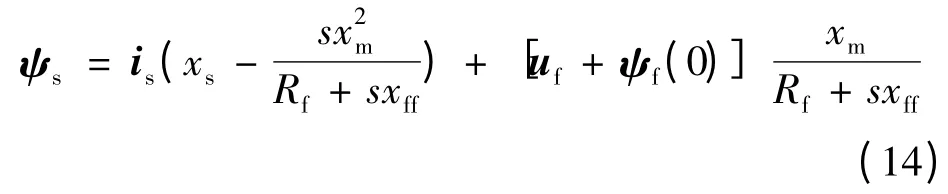
式(14)右边第一部分可以作为Laplace 域下的
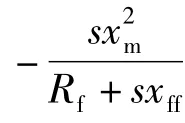
所以式(14)可简化:
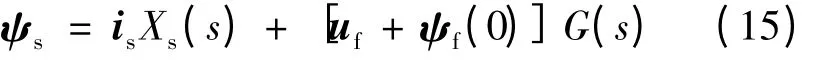
Xs(s)可以变形:
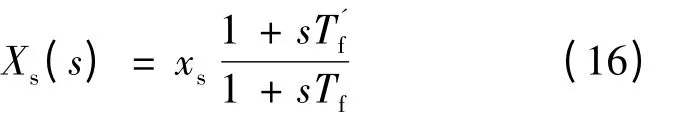
根据叠加原理,HIA 突然短路可以看成是下面两种工况的叠加:
(1)在零初始状态下,电枢端突然加上与电机短路前大小相等、方向相反的电压-Us时的运行工况;
(2)电机突然短路前的稳定运行工况,空载励磁电流If(NL)产生空载定子电压Us。
定子电流矢量可写为如下形式:

式中:is1和is2分别对应上文叠加原理中(1)、(2)工况中的定子电流矢量,因此is2=0。
励磁电流根据叠加原理同样可以写:

式中:if2是空载励磁电流If(NL)。
HIA 电枢端突加电压时,各绕组的电流和磁链初值均为0,ψs(0)=0,由于励磁绕组短路,则uf=0。则此时定子绕组磁链:

ψf(0)=0 和-Us代入式(12),由式(16)和式(19)可得:
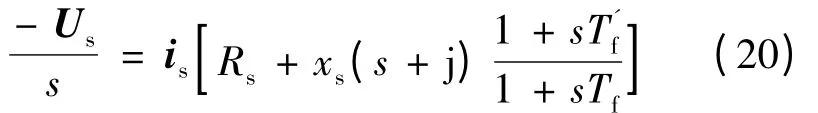
故定子电流矢量is:
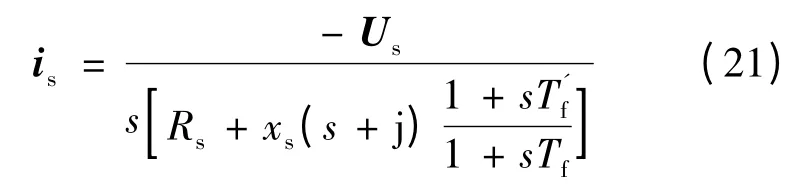
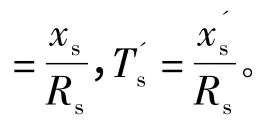
定子电流矢量用时间常数可以表示:
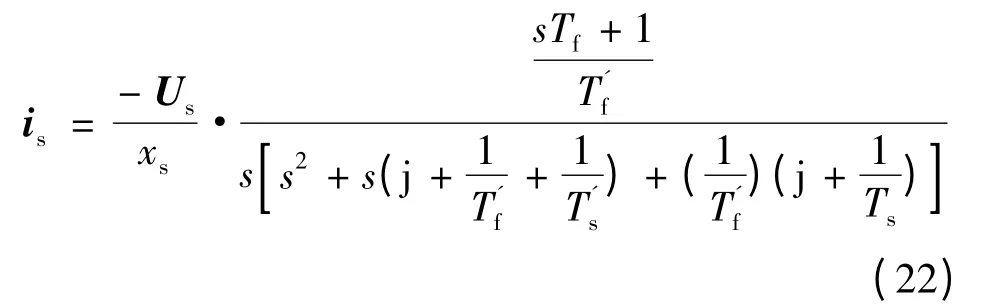
最后可以解出定子电流矢量时域解析式:
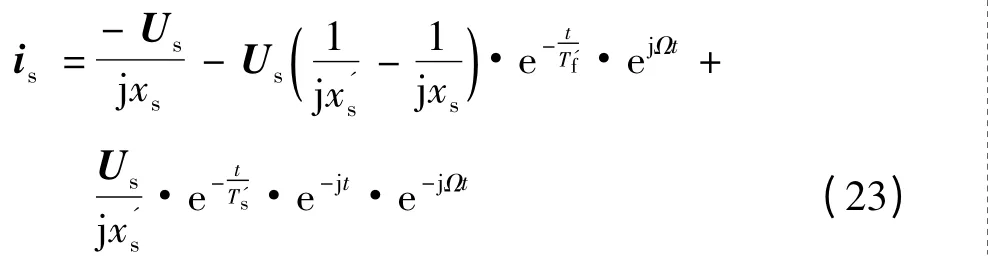
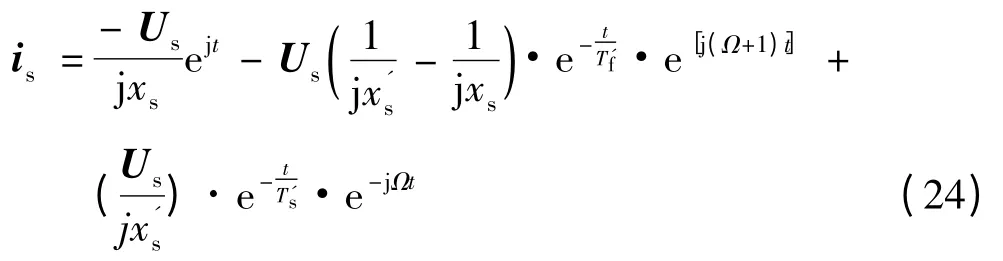
式(24)中右边第一分量表示在定子坐标系中以同步速旋转的稳态短路电流分量,没有衰减;第二分量表示旋转的定子电流矢量的瞬态分量,它是以励磁电路瞬态时间常数衰减并且在定子坐标系中以1 +Ω 的角速度旋转,其中Ω≤1。第三分量以很小的角速度(Ω≤1)旋转,可以把它看做近似停顿,并且它是以定子瞬态时间常数衰减。
从式(24)可以看出,is(+0)=0,当t >+0 和接下来的少数循环里的瞬态特性是由电抗决定。
类似的,也可以计算励磁绕组在三相短路时的电流。HIA 电枢端突加-Us时,励磁绕组短路,并且励磁绕组磁链初值ψf(0)=0,则式(13)可写:

将式(22)代入式(25),励磁电流的最终表达式:
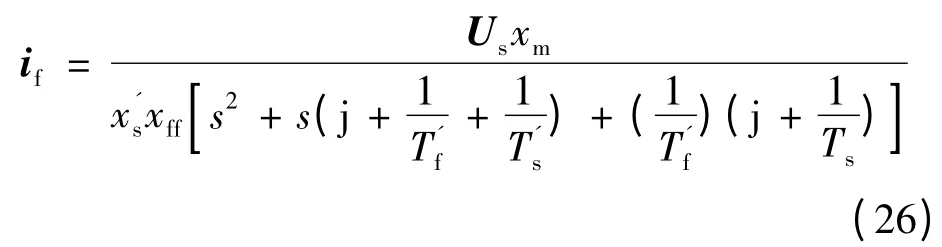
励磁绕组在转子坐标系中的电流矢量:

代入感应子发电机设计相关电感参数,电机转速n=6 000 r/min,励磁电流If=6 A 时,根据发电机定子短路电流的解析表达式(24)可以得到它的三相短路电流的解析波形以及通过电机建模和试验HIA 三相短路时C 相电流波形,如图6 所示。从图6 中可以看出,解析波形与仿真和试验的波形具有良好的一致性,从而可以论证该空间矢量法计算HIA 的三相短路电流的正确性和适用性。
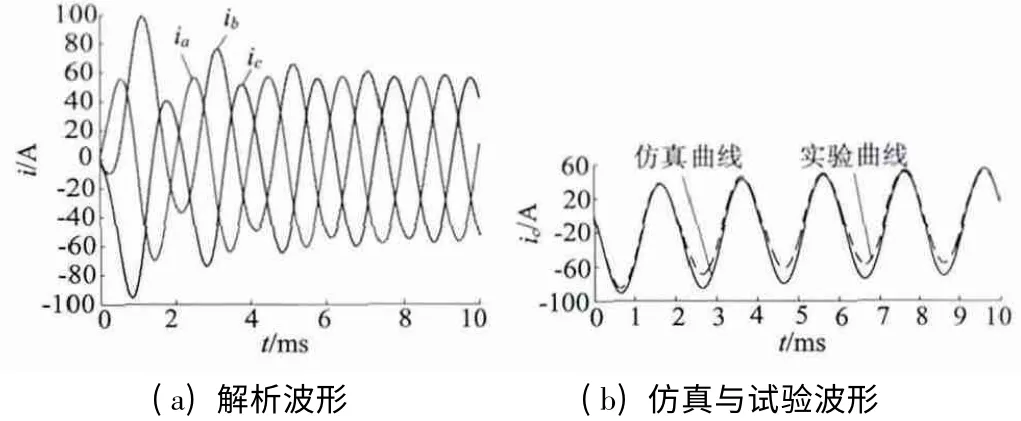
图6 HIA 三相短路电流的解析波形、仿真试验波形
4 结 语
本文通过空间矢量变换的方法推导了感应子电机三相短路时的瞬变电抗以及对应的等效电路,然后结合传统同步电机的瞬态分析计算方法,推导了感应子电机在考虑各绕组电阻情况下三相短路时定子绕组和励磁绕组电流的解析表达式,并通过HIA建模仿真和试验验证了该方法得到的解析波形的正确性,为感应子电机的瞬态分析提供了解析依据。
[1] Trutt F C,Erdelyi E A.No-load flux distribution in saturated high-speed homopolar inductor alternators[J].IEEE Transactions on Aerospace,1963,1(2):417-429.
[2] Al-Akayshee Q H,Eastham J F.A comparison between AC side excited heteropolar and homopolar synchronous machines[C]//Proceedings of the 1996 International Conference on Power Electronics,Drives and Energy Systems for Industrial Growth. IEEE,1996:530-534.
[3] Osborn G A.Design of ultra-high speed alternator systems for mobile power[J].IEEE Transaction on Aerospace and Electronic Systems,1966,2(4):103-105.
[4] Msekela J A N,Materu P N,Nzali A H.Development of a homopolar electrical machine for high power density high speed application[C]//IEEE Africon 4th Conference.IEEE,1996:184-187.
[5] 吴春九.自备电源系统高压高速脉冲交流发电机的分析与设计[D].武汉:华中科技大学,2008.
[6] Ren Zhangao,Yu Kexun.Investigation of a novel pulse CCPS utilizing inertial energy storage of homopolar inductor alternator[J].IEEE Trans on Plasma Sci.,2011,39(1):310-315.
[7] Ren Zhangao,Yu Kexun.Performance of homopolar inductor alternator with diode-bridge rectifier and capacitive load[J]. IEEE Trans on Industrial Electronics,2013,60(11):4891-4902.
[8] Siegl M,Erdelyi E A.Damper bars and their influence in operating homopolar inductor alternators for aerospace supplies-Part I:determination of saturated time-dependent reactances[J]. IEEE Transactions on Aerospace and Electronic Systems,1973(6):925-931.
[9] Siegl M,Erdelyi E A.Damper bars and their influence in operating homopolar inductor alternators for aerospace supplies-Part II:subtransient reactances of saturated homopolar inductor alternators with damper windings aerospace and electronic systems[J]. IEEE Transactions on Aerospace and Electronic Systems,1973,AES-9(6):932-939.
[10] Erdelyi E A,Trutt F C,Hopkins R E.Flux distribution in saturated high-speed homopolar inductor alternators with purely reactive loads[J].IEEE Transactions on Aerospace,1963,1(2):107-416.
[11] Erdelyi E A.Influence of inverter loads on the airgap flux of aerospace homopolar alternators[J]. IEEE Transactions on Aerospace,1965,3(2):7-11.
[12] Erdelyi E A,Jackson R F,Ahamed S V,et al.Eddy current losses in the rotor teeth of aerospace homopolar alternators[J]. IEEE Transactions on Aerospace,1965,3(2):24-31.
[13] Lou Zhenxiu,Yu Kexun,Wang Liheng,et al.Two-reaction theory of homopolar inductor alternator[J].IEEE Transactions on Energy Conver.2010,25(3):677-679.

