永磁同步电动机绕组串并联换接运行性能研究

吉 智，包西平

(徐州工业职业技术学院，江苏徐州221140)

0 引 言

永磁同步电动机具有控制性能好、体积小、效率高等优点，得到了广泛的应用。对于永磁同步电动机而言，提高高速运行时的输出转矩是扩展调速范围的关键，增加逆变器与电机的容量可以满足这一要求，却降低了传动系统低速运行时容量的利用率，增加了体积、重量和成本。采用合适的电流控制方法［1－3］，可以在一定程度上提高输出转矩，但却受凸极率及弱磁率的限制，转子结构未经特殊设计，永磁同步电动机的“弱磁扩速”的效果是很有限的。

随着新材料、转子新结构以及新型算法的涌现，永磁同步电动机的性能还可能得到进一步提高。但如何在当前技术经济条件下，大幅提高永磁同步电动机的调速比，显然是更加迫切的问题。本文提出采用定子绕组串并联换接的方法解决这一难题，只要对电机和驱动系统稍作改进，就可以在现有条件下显著提高永磁同步电动机的性能。

1 绕组串并联换接的实现

要实现永磁同步电动机定子绕组的串并联换接，需将每相设计成两套完全相同的绕组，低速时两套绕组串联，高速时两套绕组并联，其切换通过接触器或电力电子器件实现，如图1 所示。这样低速运行时，串联绕组匝数多，磁链值高，输出转矩大;高速运行时，并联绕组匝数少，磁链值低，对逆变器输出电压的要求降低，延缓了电流调节器饱和的发生。

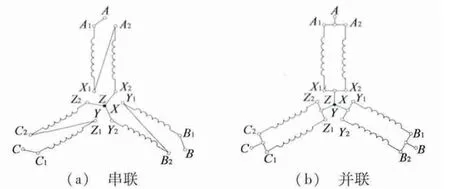
图1 绕组的串并联换接

绕组切换的过程包括三个阶段，即电流由最大值降为零的时间t1、开关器件的开闭时间t2及电流由零升为最大值的时间t3。整个换接时间为t1+t2+t3。因此对某一具体的系统来说，绕组串并联换接过程具有确定的时间长度，换接时无需检测绕组电流大小，只需根据预定的时间进行切换即可。图2 是绕组具体的连接电路，开关器件采用IGBT(保护电路未画出)，串联运行时每相的K1、K3断开，K2闭合;并联运行时K1、K3闭合，K2断开。并联和串联状态之间需要加入一个死区，以避免短路。

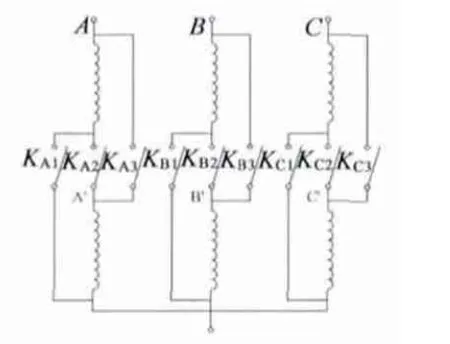
图2 换接电路

2 绕组串并联换接对电机参数的影响

绕组的串并联换接必然改变电机的参数，如电阻、电感及磁链等，在电机电压、电流极限不变的情况下，参数的变化必然带来输出转矩、转折速度等的变化。根据电工学原理，可以推导出换接前后电机基本参数间的关系如下:

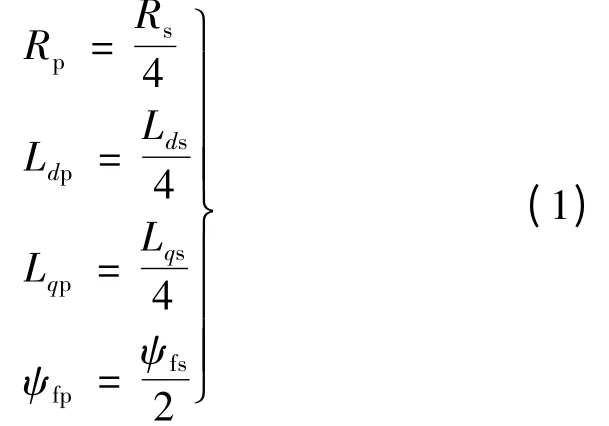
式中:下标s 代表串联，p 代表并联。定子绕组由串联变为并联后，绕组电阻、d、q 轴电感分别降至原来的1/4，磁链降低至原来的1/2。由于绕组并联时电机运行于高速区域，而电机高速运行时，电阻压降和反电动势相比很小，因此为了简单起见，不计电阻，可得:

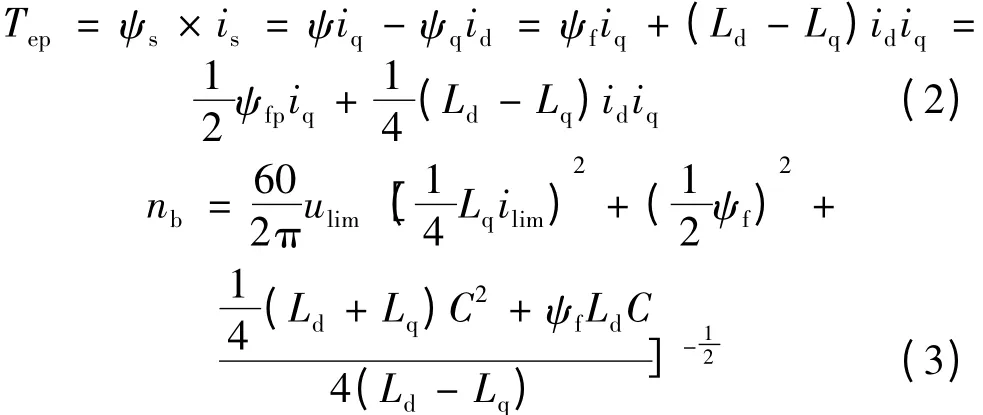
式中:

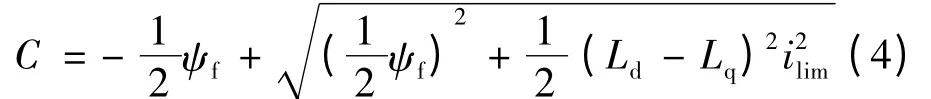
可以看出，在电流不变的条件下，定子绕组由串联变换为并联后，电磁转矩变小，转折速度变大。其中永磁转矩变为原来的1/2，磁阻转矩变为原来的1/4。

3 绕组串并联换接的仿真研究

3.1 永磁同步电动机的有限元模型

原型电机为110ST－M08020 型永磁同步电动机，转子采用面装式永磁体，永磁体牌号为N35SH，定子、转子均采用DW465_50 硅钢片，定子绕组采用星形连接，具体参数如表1 所示。将原型电机拆解测绘后在Ansoft 15 软件中建模［4］，按照要求进行运动、激励、剖分、材料、坐标系、充磁等项目的设置后即可完成建模，作为绕组串联的电机模型。然后将其定子并联支路数由1 修改为2，即可得到绕组并联电机模型。为了直观起见，本文采用全模型进行分析，完整的模型如图3 所示。

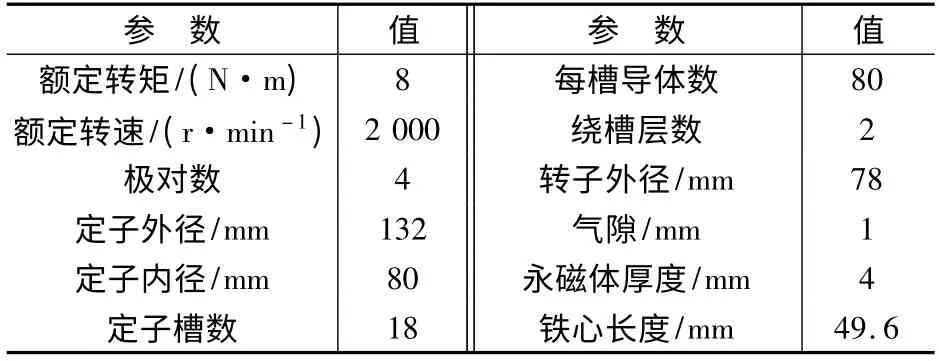
表1 实验电机参数

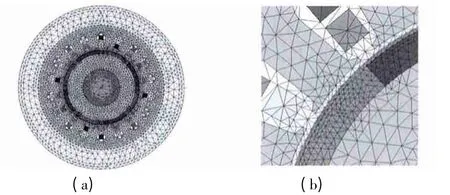
图3 电机模型与剖分

采用此模型可算出电机同步电感［5］:

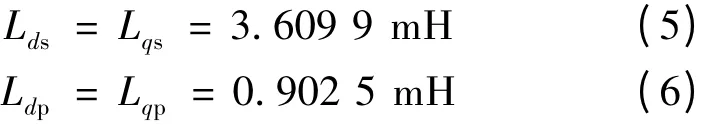
从上面的计算结果可见，定子绕组由串联变换至并联，电机d、q 轴电感变为原来的1/4，验证了前面的理论计算结果。

3.2 绕组串并联换接的静态仿真

3.2.1 永磁磁链与端电压

通过对模型进行瞬态有限元分析即可获得永磁磁链与端电压。设定电机转速为1 500 r/min，电流激励为零，相当于模拟永磁同步电动机运行于反拖发电输出开路的状态，结果如图4 所示。可见定子绕组串联时电机永磁磁链和端电压的幅值分别为0.1 Wb 和64.27 V，定子绕组并联时电机的永磁磁链和端电压的幅值分别为0.05 Wb 和32.13 V，因此定子绕组由串联变换至并联，电机永磁磁链和端电压均变为原来1/2。

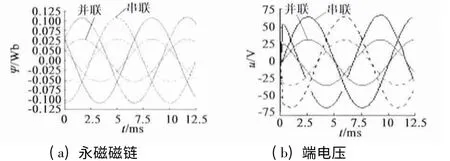
图4 定子绕组串、并联时的永磁磁链与端电压

3.2.2 输出转矩

电机输出转矩分析采用施加电流激励的瞬态有限元模型，对于低速区域可选取375 r/min、562.5 r/min、750 r/min 三个速度点分析，对应不同的速度，将相电流设置为不同的角频率即可得到输出转矩曲线，如图5 所示。可见在不同转速下，绕组串联电机输出转矩均为4.4 N·m，绕组并联电机输出转矩均为2.2 N·m。因此在低速恒转矩区域，电机输出转矩主要受极限电流的限制。当极限电流一定时，绕组串联运行有利于提高电机转矩输出能力。

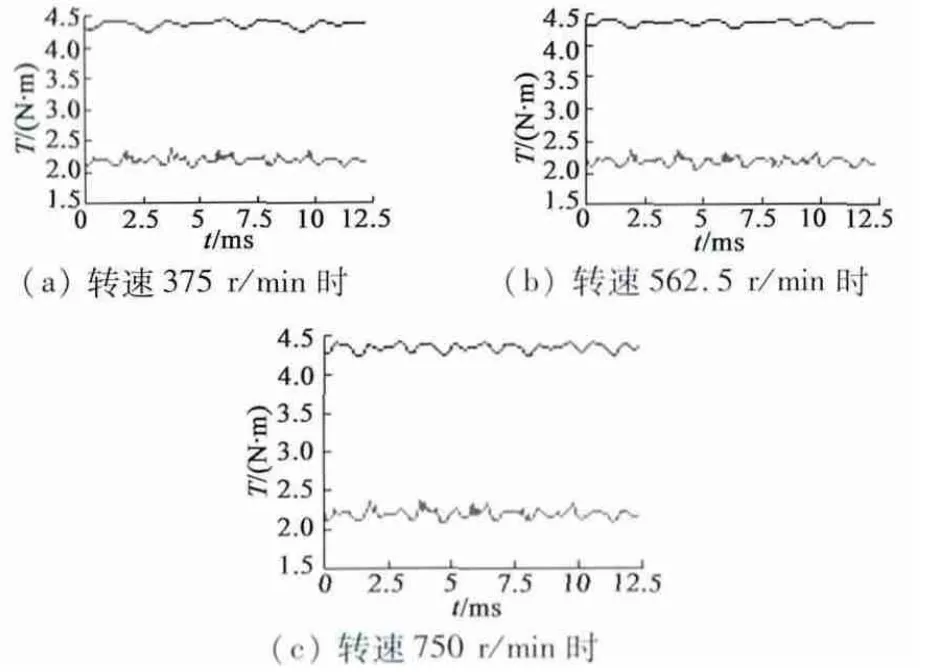
图5 不同转速时的输出转矩

仿真高速区域的输出转矩比较复杂，为了保证串、并联时电机均处于弱磁区域，要在转速高于绕组并联电机转折速度的区域进行比较实验，选取3 750 r/min、4 500 r/min、6 000 r/min 三个速度点进行分析。施加电压激励，对应不同的速度，将电压设置为不同的角频率即可得到输出转矩。对于电压激励，功角不同，电机的输出转矩是不同的，在此应当比较最大转矩。因此将功角设置为可变参数，对功角进行参数化扫描分析，以求出不同功角对应的输出转矩，并取其中最大值进行比较。表2 是部分结果，其中带阴影的数据为最大转矩。可见，在高速区域，绕组无论采用串联还是并联的形式，随着转速的增大，输出转矩均明显降低，但在相同转速的情况下绕组由串联变换为并联后输出转矩明显增大，并且转速越高，这种增大的幅度越显著。因此在高速区域将电机绕组由串联切换至并联，对于提高电机的转矩输出能力是很明显的。

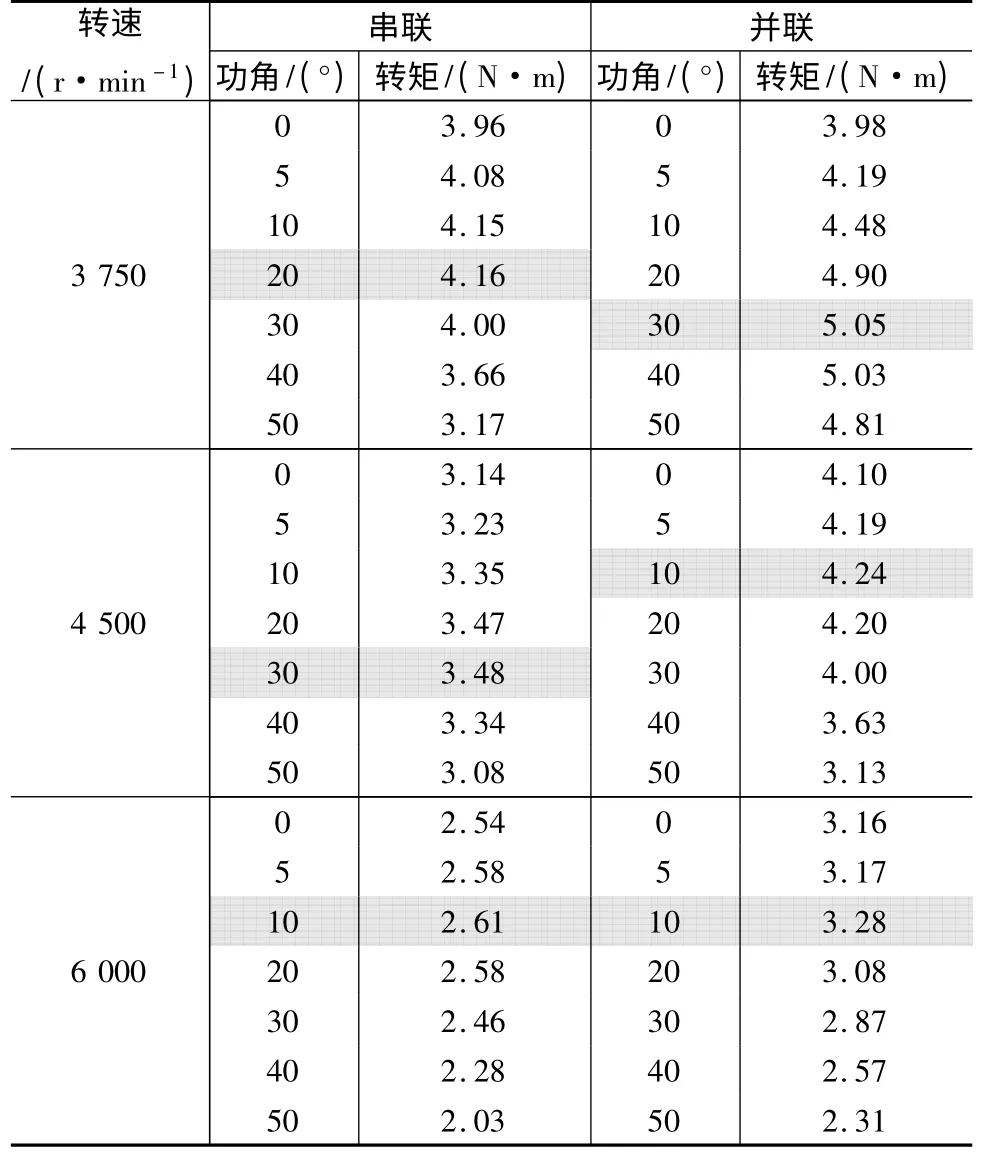
表2 输出转矩

3.3 绕组串并联换接的动态仿真

动态仿真采用MATLAB 软件，由于MATLAB 自带的电机模型不支持仿真过程中改变参数，因而重新构建电机模型，如图6 所示。只要将电机的转速反馈入id、iq以及转矩计算模块，当到达切换速度时能够自动修改电机参数即可。将转速调解器参数、电流调解器参数、逆变器参数、负载大小等固定不变，为了简便起见，电流控制算法固定为id=0 算法。

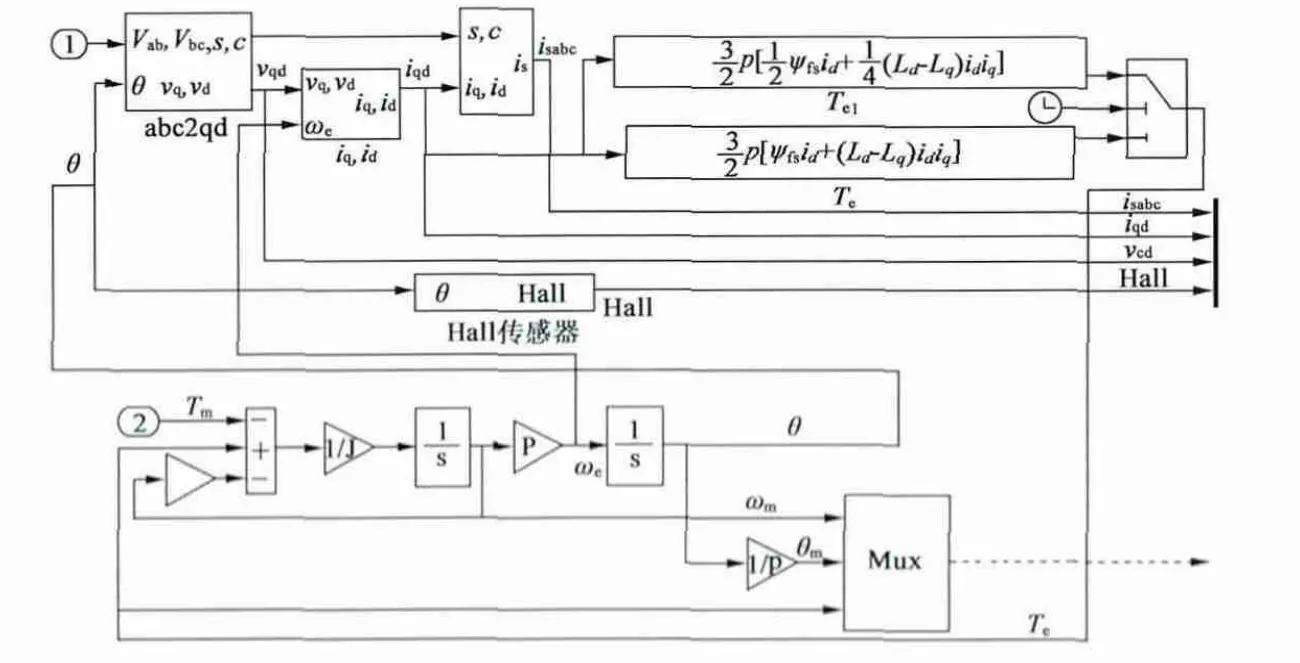
图6 能够实现绕组串并联切换的电机模型

3.3.1 换接点的确定

确定换接点的方法有两种，一种方法是采用离线的方式，对于确定的电机来说，极限电流、电压确定后，转矩转速曲线是确定的，和负载无关，所以两电机转矩转速曲线的交点是固定不变的，可以以预先设定的转速为依据切换;另一种方法是采用在线的方式，在控制器中计算电机的输出转矩，当绕组串联和绕组并联输出转矩相等时即是切换点。当然考虑到相交的是一个区域而不是一个点，在交点处可附加一个偏移量修正。按照第一种方法从图7 确定交点为(1 648 r/min，7.459 N·m)。

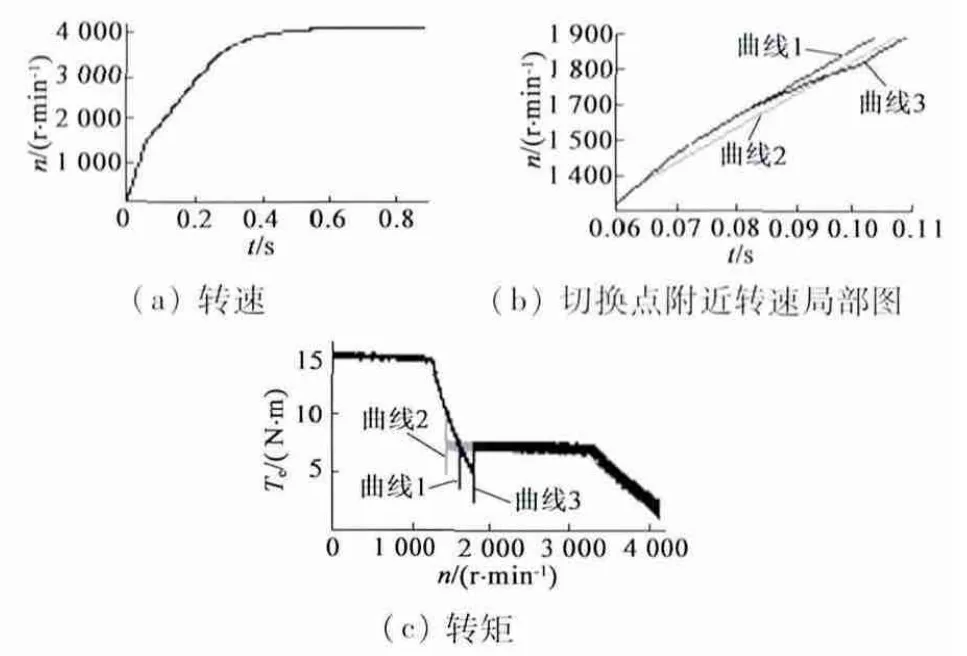
图7 切换点的确定

将负载转矩设定为额定转矩，切换点速度仍为1 648 r/min，在图7 上对应曲线1。将切换点分别向低速和高速方向平移10%，即以1 483 r/min 和1 813 r/min 为切换点，分别对应曲线2 和曲线3，图7(b)是图7(a)的局部放大。可见切换点偏离后，对系统运行的影响体现在两个方面:第一，造成加速性能下降，切换点无论超前还是滞后都会造成高于切换点的速度区域比原来的速度有所降低，加速时间变长，但对于理论最高转速并无影响;第二，造成机械冲击，因为无论切换点超前还是滞后都会造成输出转矩的突变，引起机械冲击，但由于电机工作时，轴上等效惯量比较大，输出转矩突变造成的冲击影响有限，因此切换点的确定一般并不需要非常精确。

3.3.2 空载工况下的串并联切换研究

将负载转矩设为零，为了对比同时将m0(串并联换接)、m1(绕组串联)和m2(绕组并联)三个电机所得结果画在同一张图上。

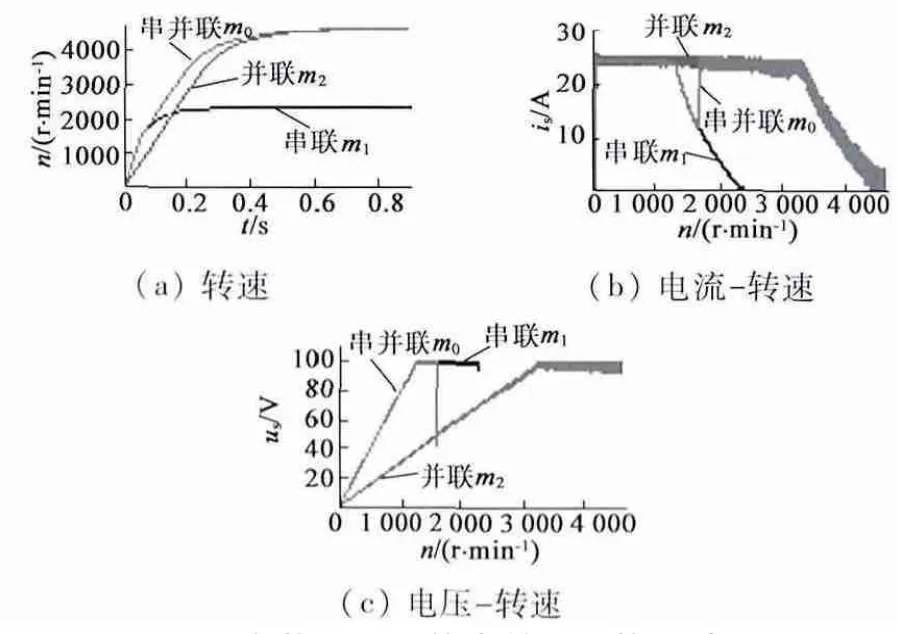
图8 空载工况下的串并联切换曲线

从速度时间曲线可见，m0电机最高运行转速和m2电机基本一致，较m1电机最高运行转速增大一倍。速度高于切换点的区域，m0和m2电机特性曲线的斜率相同，说明输出转矩相等。m0能够比m2更快地从静止起动至某一转速，例如达到500 r/min转速，m0较m2的时间缩短49.3%。产生这种现象原因在于切换点以下区域m0比m2输出转矩要大，经过一定时间的累积后体现为速度的不同。

从电流转速曲线可见，m0电机在切换点以前，电流曲线和m1完全重合，在切换点处发生跃变，大幅增加至和m2电机电流曲线重合，同时电流的波动幅度明显增大，这是由于绕组由串联切换至并联后，电流调节器退出饱和，电流重新跟踪给定值，绕组电感大幅降低至原来的1/4，从而造成电流变化更加剧烈。

从电压转速曲线可见，m0电机在切换点以前，电压随着转速的增大线性增大至极限电压，电压曲线和m1电机电压曲线完全重合，在切换点处发生跃变，大幅下降至和m2电机电压曲线重合，然后继续随转速的增大线性增大至极限电压。

从以上分析可见，在切换点以下的转速，m0电机绕组串联运行，其特性和m1电机一致;在切换点以上的转速，m0电机绕组并联运行，其特性和m2电机相似。绕组串并联切换技术利用了低速区域绕组串联输出转矩大，高速区域绕组并联运行极限转速高两个方面的优势，解决了电机随着转速增大端电压增至极限电压造成电流调节器饱和，输入电流降低，从而输出转矩下降的问题。

3.3.3 负载工况下的串并联切换研究

将负载转矩设定为额定转矩(2.2 N·m)，仿真结果如图9 所示。m0在额定负载和空载下，其转矩－转速、电流－转速、电压－转速曲线基本重合，区别在于最高转速略有不同，从4 632 r/min 降至4 133 r/min;转速－时间曲线不重合，表明额定负载下加速的时间有所变长;另外负载的大小对于切换点的确定没有任何影响，切换点对应的速度和转矩均不变，但由于运行时的速度发生了变化，因而切换点处对应的时间不同了，所以确定切换点时不能以时间为依据，而应当如前文所述以速度或转矩为依据。

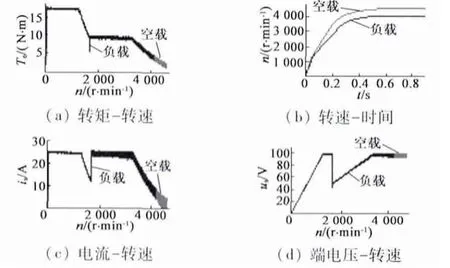
图9 负载工况下的串并联切换曲线

4 绕组串并联换接的实验研究

绕组串并联换接实验平台如图10 所示，由电机及驱动器、编码器、制动器、转矩转速与电参数采集系统、计算机以及数据采集软件构成［6－7］，其中电机为110ST－M08020 型电机，串并联换接器件采用开关频率较高的IGBT。实验分为空载和负载两种情况，速度给定值均为6 000 r/min，负载实验的负载转矩为0.8 N·m，图11 和12 分别为空载和负载实验结果。为了更加清晰，线电压画出三相，相电流只画出A 相。图11、图12 中，其转速、转矩则将串联、并联和串并联切换三种情况叠加在一张图上显示。

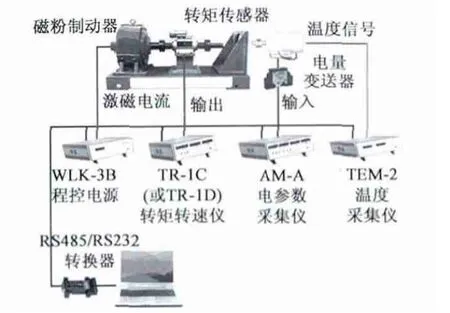
图10 实验系统构成

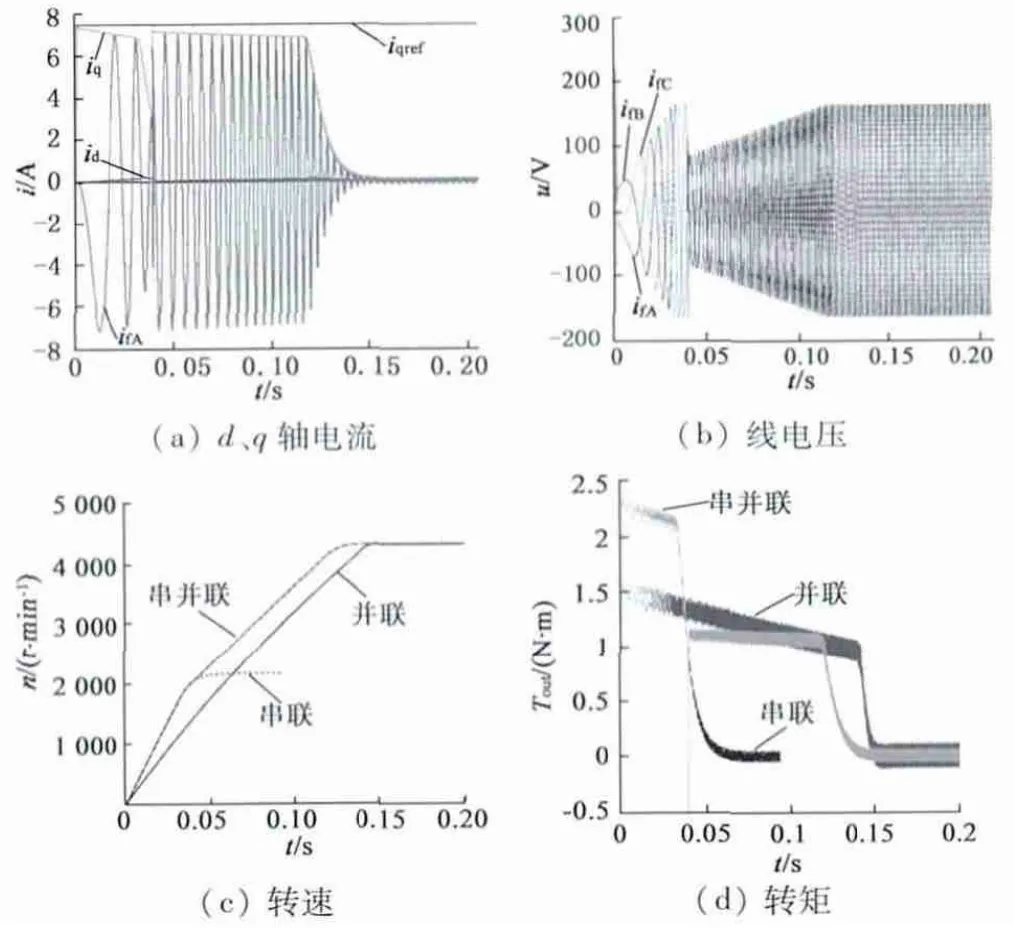
图11 空载实验曲线

图12 负载实验曲线

从图中可见，绕组串联运行最高转速为2 158 r/min，并联运行和串并联换接运行最高转速一致，均为4 324 r/min，大约提高了一倍。串并联切换电机在低速时的转速、转矩特性和串联运行电机一致;超过切换点后，运行趋势基本和并联运行平行，但速度上升更快，所能达到的最高转速则和绕组并联电机相同。以上分析还可以从电流、电压图中得到佐证，绕组串联低速时输出转矩大，但端电压增长快，在速度较低时端电压即达到电压限幅值，q 轴电流逐渐偏离给定值，电流调节器饱和，输出转矩急剧下降。但切换为并联后端电压回落至电压限幅以下，q轴电流又重新进入被控状态。负载工况的实验结果和空载工况基本一致，由于存在负载转矩，电机的加速度减小，加速时间延长，达到给定转速后q 轴电流不为零，和空载工况相比，其结果曲线相当于在时间上向后发生了平移。

在实验中输出转矩在切换点处发生了大幅跌落，这是由于切换时电流失控造成的，失控的时长为开关时间与死区时间之和。但从以上实验结果来看，切换时的电流失控没有对电机的运行状态产生明显的影响。这是因为一方面电流失控时间非常短，另一方面电机转子本身转速很高，惯性较大，因而对这种短暂、单次的扰动并不敏感。

5 结 语

对于高性能永磁同步系统，既要求低速大转矩，又要需要高速大功率。从电磁设计角度来看，这两种要求是矛盾的，本文提出一种定子采用两套绕组，根据需要在运行中两套绕组串并联切换，以扩展电机运行速度范围的方法。

本文论述了永磁同步电动机绕组串并联换接的实现方法，对串并联换接造成电机参数的变化、换接前后电机性能的变化进行了理论分析;通过仿真对以上分析结论进行了验证，并确定了以转矩相等为原则决定换接点。结合实物实验，可以得出以下结论:绕组串并联换接可以大幅度扩展永磁同步电动机的运行范围，换接的时刻、换接过程对电机运行的影响并不显著，在应用条件许可的情况下绕组串并联换接是扩展速度范围的有效方法，较好地解决了同一台电机既要求低速大转矩，又要求高速大功率这一矛盾。

［1］ Vaclavek P，Blaha P. Interior permanent magnet synchronous machine field weakening control strategy－the analytical solution［C］//Proceeding of international conference on electrical machines and systems.2007，Seoul，Korea:440－445.

［2］ 吉智，何凤有. 凸极永磁同步电机电流控制方法研究［J］. 电气传动，2011(7):3－7，24.

［3］ 李长红，陈明俊，吴小役. PMSM 调速系统中最大转矩电流比控制方法的研究［J］. 中国电机工程学报，2005，25(21):169－174.

［4］ 刘国强，赵凌志，蒋继娅. Ansoft 工程电磁场有限元分析软件［M］.北京:电子工业出版社，2005.

［5］ 石文娟，王艾萌，李和明. 内置式永磁同步电机磁路饱和特性分析与补偿的研究［J］.华北电力大学学报，2010，37(6):12－16.

［6］ 吉智，何凤有，窦春雨. 基于Matlab/Xpc Target 的实时数据采集系统设计［J］.工矿自动化，2009，158(5):74－77.

［7］ 王成元，夏加宽，杨俊友，等.电机现代控制技术［M］.北京:机械工业出版社，2006.