一种利用非差单点定位的卫星定位基线解算新方法

祝会忠，徐爱功，高星伟，冯彦同

（1.辽宁工程技术大学 测绘与地理科学学院，辽宁 阜新 123000；2.中国测绘科学研究院，北京 100830；3.山东省国土测绘院，济南 250102）

1 引言

在测站数量较多的卫星定位大网解算的数据处理中，如果对整网进行解算，计算量大，耗时长，也限制了对所有可用观测数据的充分利用。如果在每个测站上按单点定位模式进行数据处理，计算速度会明显提高。使用单点定位的方法，n个测站的处理时间为O（n），而整网处理模式的处理时间大约为O（n3）。采用单点定位模式进行卫星定位网数据处理的耗时是随着测站数量线性变化的。

由于采用了单点定位的数据处理方法，这就需要以单点定位结果为基础获取站间基线，然后进行卫星定位网解算。如果根据单点定位的结果直接计算基线向量，采用精密单点定位（precise point positioning，PPP）模式时，需要全球卫星导航系统国际服务协会（international global navi－gation satellite system serviceIGS 提供的精密星历和卫星钟差，而且只有在计算收敛之后才能得到较高精度的点位信息。利用非差单点定位得到的结果直接计算站间基线，其精度取决于单点定位的精度。若不采用PPP，则单点定位结果的精度很差。非差单点定位的误差影响较多，无法采用差分的方法消除或削弱误差影响，要得到高精度的定位结果，必须利用完善的改正模型对各种误差加以改正。为了快速、准确地得到高精度的定位结果，本文提出一种利用卫星定位非差单点定位的测站间基线解算新方法。实验表明：新方法可在非差单点定位数据处理中进行测站间基线的快速准确解算。

2 基线解算新方法

利用卫星定位非差单点定位结果进行测站间基线解算的新方法的基本思想是：首先，在各测站上进行非差相位单点定位数据处理，获取每个站的非差法方程。对于需要解算的基线向量，提取相应两个基线端点的非差法方程进行投影变换，再将测站法方程进行组合。得到测站坐标差和相关模糊度组合的法方程。然后利用分步搜索的最小二乘降相关分解 法（least－square ambiguity decorrelation adjustment，LAMBDA）进行模糊度固定和基线解算。

2.1 非差相位单点定位的数学模型

测站上线性化的卫星定位非差载波相位观测方程可表示为

式中，φi为载波相位观测值，λi为载波相位波长，ρ0为卫星到测站间的几何距离，［lmn］为方向余弦，［ΔXΔYΔZ］T为坐标改正数，tR为接收机钟差，tS为卫星钟差，Ni为载波相位的整周模糊度，i表示频率，Vion为电离层延迟，Vtrop为对流层延迟，δρ为卫星星历误差对测距的影响，Vmul为多路径误差，ε为观测噪声。

当观测到多颗卫星时，观测方程（1）误差方程组的矩阵形式为

式中，V残差向量，A为系数矩阵，X为参数向量，L为观测值向量，ε为随机噪声。

采用最小二乘估计方法进行参数估计，法方程为

式中，N＝ATPA，W＝ATPL，P为权阵。

2.2 测站非差单点定位法方程的变换

测站非差单点定位法方程的变换可采用一个变换矩阵进行法方程变换，其变换过程如下：

非差单点定位数据处理中参数向量的方差协方差矩阵Q为：Q＝N－1，并有

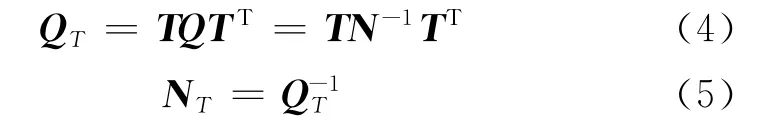
转换后的法方程设为：NTXT＝WT，则有

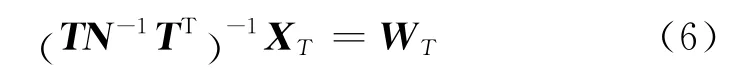
式（6）即为非差单点定位法方程转换后得到的新法方程，其中XT为转换后的参数向量，T为从X到XT的转换矩阵。

另外，还可以只考虑位置参数和模糊度参数，对非差单点定位法方程中相应的元素进行变换得到新的法方程。

2.3 测站间法方程的组合

测站上的非差定位法方程经过变换后，再将两个测站上的法方程进行组合。如果有两个测站A和B，测站A、B经过转换后的法方程分别为

式（7）中的第二式两边同乘以NANB－1，进行变换可得

将NAXA＝WA与式（9）相减得

式（10）即为整合后的法方程，假设测站A，B上只考虑了位置参数和模糊度参数，上式中（XA－XB）为新参数向量，包含测站间的坐标差和模糊度差，即为

令 ΔXYZ＝［ΔXA－ΔXBΔYA－ΔYBΔZAΔZB］T，ΔN＝ ［N1A－N1B…NnA－NnB］T

将两个测站上的模糊度组合ΔN作为新模糊度进行模糊度固定，新组成的模糊度参数固定之后再计算两测站坐标差的固定解。

2.4 模糊度固定方法

为了缩小模糊度搜索空间，保证模糊度ΔN解算的成功率，对常规的LAMBDA方法进行改进，在LAMBDA方法搜索结果的基础上再进一步固定模糊度。具体过程如下：

1）根据法方程式（10）得到ΔN的方差协方差矩阵，并对其进行最小二乘降相关处理。按照常规LAMBDA方法中搜索空间的构造方法来建立模糊度的搜索空间，然后搜索出k组模糊度组合。搜索方法也与常规的LAMBDA搜索方法一致，只是搜索出的不是唯一的一组模糊度，而是依次按LAMBDA方法搜索出最优的k组模糊度组合构成新的模糊度搜索空间。k的大小与浮点解精度成反比。

2）将k组模糊度组合组成的模糊度搜索空间中的所有备选组合进行回代计算，得到ΔXYZ及相应的残差向量VL，并计算方差因子σ20＝为ΔXYZ方差协方差矩阵，n为观测值向量的维数。

对得到的k个σ20值进行Ratio检验

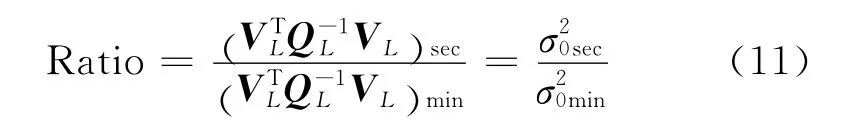
若Ratio大于某一限值（一般取为大于2的常数），则认为方差最小值所对应的模糊度参数组合为正确的模糊度组合。

2.5 测站间基线向量的确定

将模糊度组合ΔN作为新模糊度固定之后，再计算ΔXYZ。由ΔXYZ可得到两测站站间的基线长度l为

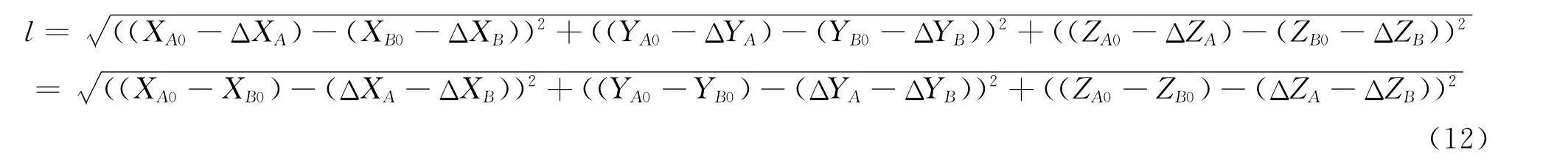
式中 ［XA0，YA0，ZA0］T和 ［XB0，YB0，ZB0］T分别为测站A和B的初始坐标。因为ΔN作为新模糊度已经固定，所以l已经具有较高的精度。根据ΔXYZ能确定两站间的相对位置关系。在已经得到测站间相对位置关系的情况下，要得到两站间基线向量，需要确定一点在参考框架下的准确坐标，也就是在整网中引入一个起算点。最直接的方法是其中一点为WGS84框架下的已知点；也可将一点与国家高精度卫星定位点进行联测，最好与周围的IGS站进行联测，这些站点的坐标和观测资料一般均可从IGS网站上免费取得，无需设站观测，或是利用其它连续运行的基准站。

3 实验算例与分析

为了验证本文的算法，采用两组数据进行实验，实验数据均为2008－01－02的观测数据，卫星定位时为54 467d。第一组为一条短基线间两点的观测数据，第二组是一个连续运行参考站（continuously operating reference stations，CORS）网中三个基准站的观测数据。五个点的观测数据都从54 467d0h开始记录，观测时间为2～3h，各点的坐标已知，便于对计算结果进行精度评定，各基线信息如表1所示。

使用本文的方法在各站非差单点定位数据处理中进行基线解算。与各基线对应的两个测站的模糊度组合ΔN固定之后，解算出的每条基线（基线长度）与已知坐标提供的基线真值进行比较，结果如下图1～图4所示。在对各测站实验数据进行单点定位数据处理时，使用的是广播星历，采用Saastamoinen模型改正对流层延迟，并利用无电离层组合观测值。

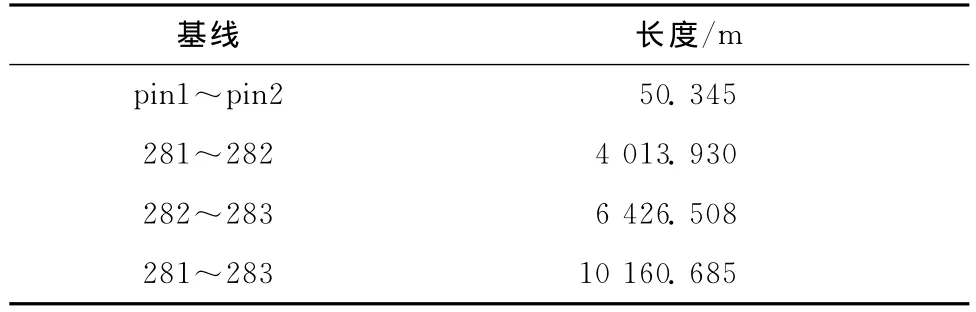
表1 实验基线信息

图1 基线pin1～pin2的解算精度

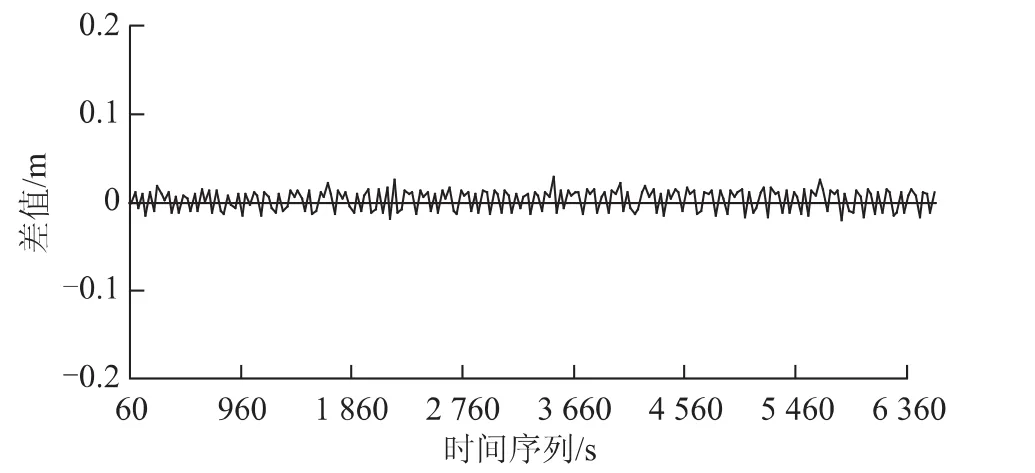
图2 基线281～282的解算精度

图3 基线282～283的解算精度

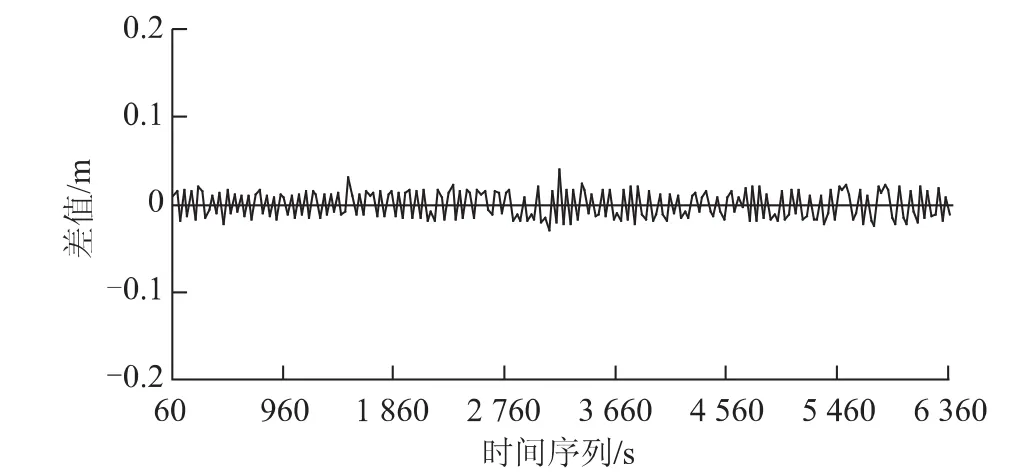
图4 基线281～283的解算精度

从图1～图4可以看出，基线的解算精度都到达或优于厘米级，该精度与利用双差模式进行基线解算的精度相当。按照上述误差处理策略进行计算，法方程变换组合后各项误差还存在一定的残差，但不会影响使用广播星历实时得到厘米级的基线解算精度。在测站数量较多的卫星定位网解算中，一般都是采用精密单点定位模式，使用了比较完善的误差改正模型。这种情况下，新模糊度组合的浮点解精度得到大大提高，新模糊度的搜索空间会很小，相比非PPP模式的单点定位模糊度搜索速度大大加快，模糊度固定所需观测时间也会缩短。另外，如果在PPP计算得到高精度解之后通过取整来固定模糊度，虽然避免了搜索计算带来的少量计算机耗时，但这种做法需要较长的观测时间，所以，采用本文的基线解算新方法通过模糊度搜索可进行基线的快速准确解算。

4 结束语

本文中的基线解算方法是在对非差单点定位法方程进行变换的基础上，组合测站间的法方程，通过分步搜索方法将模糊度固定，进而解得测站间基线，能快速、准确地计算出高精度的基线结果，可得到与双差定位模式相当的基线解算精度。该方法与采用双差观测值的基线解算方法相比还具有可用观测值多、数据利用率高、保留了更为丰富的观测信息等优点。精密单点定位中使用了较为完善的误差改正模型，在此基础上使用本文的方法，能够减少高精度基线解算所需的观测时间，大大缩短模糊度固定的搜索时间，提高模糊度解算效率。将该方法应用到卫星定位大网解算中可以快速准确地解算站间基线，提高网解的解算效率和精度，而且便于在已有的观测网中增加新测站和去除某些测站，不需要重新处理所有的数据。

［1］ BLEWITT G.Fixed Point Theorems of GPS Carrier Phase Ambiguity Resolution and Their Application to Massive Network Processing：Ambizap［J］.Journal of Geophysical Research，2008，113（B12410）：1－12.

［2］ GE Meng－rong，GENDT G，DICK G，et al.Improving Carrier－phase Ambiguity Resolution in Global GPS Network Solutions［J］.Journal of Geodesy，2005，79（1－3）：103－110.

［3］ GE Meng－rong，GENDT G，DICK G，et al.A New Data Processing Strategy for Huge GNSS Global Networks［EB／OL］.［2013－08－25］.http：／／center.shao.ac.cn／shao＿gnss＿ac／publications／A%20New%20Data%20Processing%20Strategy%20for%20Huge%20GNSS%20Global%20Networks.pdf.

［4］ TEUNISSEN P J G.The Least－squares Ambiguity Decorrelation Adjustment：A Method for Fast GPS Integer Ambiguity Estimation［J］.Journal of Geodesy，1995，70（1－2）：65－82.

［5］ 祝会忠，刘经南，唐卫明，等.快速解算长距离网络RTK参考站间双差模糊度的算法研究［J］.武汉大学学报：信息科学版，2012，37（6）：67－71.

［6］ 唐卫明，孙红星，刘经南.附有基线长度约束的单频数据单历元LAMBDA方法整周模糊度确定［J］.武汉大学学报：信息科学版，2005，30（5）：444－446.

［7］ 祝会忠，高星伟，徐爱功，等.网络 RTK流动站整周模糊度的单历元解算［J］.测绘科学，2010，35（2）：78－79.

［8］ 高星伟，刘经南，葛茂荣.网络 RTK基准站间基线单历元模糊度搜索方法［J］.测绘学报，2002，31（4）：305－309.

［9］ 祝会忠，刘经南，唐卫明，等.长距离网络 RTK基准站间单历元整周模糊度确定方法［J］.测绘学报，2012，41（3）：359－365.

［10］ 祝会忠，高星伟，秘金钟，等.一种 GPS整周模糊度单历元解算方法［J］.测绘科学，2011，36（4）：9－11.