Sage-Husa随机加权无迹卡尔曼滤波及其在导航中的应用
侯 俊,朱长青,2,阎海峰,3,高社生
(1.西北工业大学 自动化学院,西安 710072;2.空军装备部 科研订货部机载处,北京 100843;3.中航工业集团 深圳南航电子工业有限公司,广东 深圳 518052)
1 引言
无迹卡尔曼滤波(unscented Kalman filter, UKF)是以无迹变换为基础,以标准卡尔曼滤波算法为框架,采用确定性采样的一种近似线性最小方差估计方法。该算法具有实现简单、滤波精度高、收敛性好等优点。然而UKF要求精确已知噪声的先验统计特性,在实际应用中,受到试验样本的限制或内外部不确定因素的影响,噪声的先验统计是未知或不准确的,使得传统UKF的应用受到限制。Sage滤波不需要给出动力学模型噪声先验协方差矩阵,就可以估计出状态预报向量的协方差矩阵。但是,所给定的模型噪声先验协方差矩阵是特定时间窗口内模型误差的平滑值。当动力学模型存在较大的异常扰动时,用开窗平滑法求出的状态预测信息的协方差矩阵不能反映模型误差的实际大小[1-4]。文献[1]等提出了一种改进的Sage自适应滤波算法,即利用Sage滤波的开窗平滑法求得状态预测信息的协方差矩阵,然后用自适应因子进行调节。但文献[1]中在求观测残差向量和新息向量(预测残差向量)的协方差阵时,对观测残差向量和新息向量均采用算术平均值法,没有区分各个历元观测残差向量值和新息向量值的大小,因而估计精度不高。随机加权法是一种非常实用的统计计算方法,该方法具有计算量小、估计精度高、具有良好的大样本性质,不需要知道统计量的概率分布等优点,被广泛应用于电子信息,自动控制和航空航天等领域导航参数的估计。与文献[1]中所采用的算术平均值法比较,随机加权法能根据观测信息和新息向量的有用程度,选取不同权值,增强对有用信息的利用,从而提高滤波解算精度。
本文在吸收Sage-Husa滤波和UKF优点的基础上,提出一种非线性Sage-Husa随机加权无迹卡尔曼滤波(Sage-Husa random weighting unscented Kalman filter, SRWUKF)算法,该方法利用Sage滤波的开创平滑方法求得观测残差向量和新息(预测残差)向量的协方差阵。然后用随机加权自适应因子对观测残差和预测残差进行调节,对状态预报向量的协方差矩阵进行自适应随机加权估计,以控制观测残差和预测残差对导航精度的影响。最后对UKF、自适应无迹卡尔曼滤波(adaptive unscented Kalman filter, AUKF)和本文所提出的SRWUKF三种算法进行了计算和比较分析。
2 随机加权法的基本思想
设X1,X2,…,Xn是来自分布函数F(x)的独立同分布样本,相应地经验分布函数

(1)
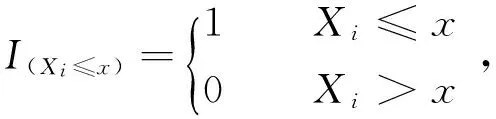
f(v1,v2,…,vn-1)=Γ(n),
(v1,v2,…,vn-1)∈sn-1
3 非线性Sage-Husa随机加权极大验后估值器
考虑如下离散非线性系统
(2)
式(2)中,Xk∈Rn为k时刻系统的状态向量,f(·)是状态向量的非线性函数,Wk∈Rn为系统过程噪声,Zk∈Rm为k时刻系统的量测输出,Vk∈Rn为观测噪声,Bk为系统观测矩阵。
假设系统过程噪声Wk和观测噪声Vk为相互独立,均值和协方差阵为时变的正态白噪声序列,统计特性满足
(3)
式(3)中,q和r分别为Wk和Vk的均值,Q和R分别为Wk和Vk方差阵,q、r、Q和R均是未知的,δk,j为示性函数。
则Sage-Husa的噪声统计估值器为
(4)
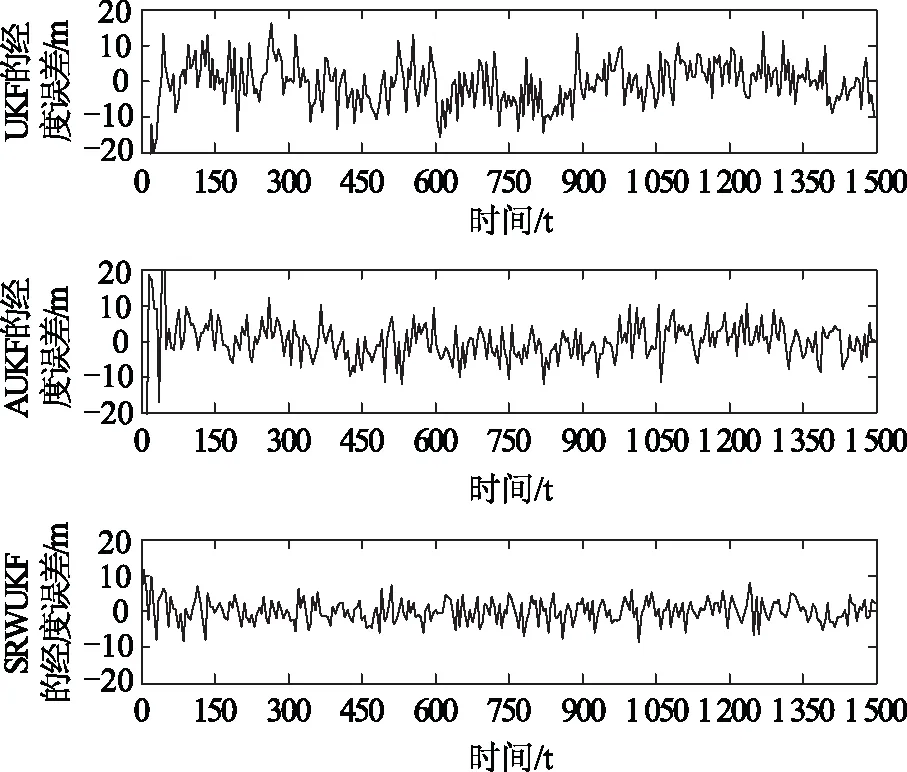
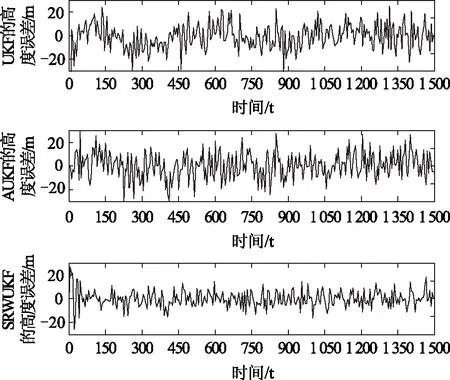
式(4)中,dk-1=(1-b)/(1-bk),0 对于式(2)所描述的非线性系统,根据极大验后噪声统计估值的定义,可得q,r,Q和R的算术平均值估计为 (5) 相应地,q,r,Q和R的随机加权估计为 (6) (7) 式(7)所表示的非线性Sage-Husa随机加权极大验后估计器是次优的。 工程实际中,动力学系统的过程噪声和观测噪声的方差阵Q和R对UKF的滤波精度有严重影响,这是由于Q和R决定了当前信息和前一时刻观测信息之间的权重。而当前信息和前一时刻的观测信息又将直接影响UKF的递推精度。由此可见,动力学系统的过程噪声和观测噪声中的任何偏差,都将导致滤波变为次优,甚至可能出现发散。为此,本文提出一种非线性Sage-Husa随机加权UKF算法,该算法的步骤为 (1)初始化 初始化后的滤波值为 (8) 和 (9) (2)计算Sigma点 (10) 非线性变换产生的样本点为 (11) (3)时间更新 状态的一步预测为 (12) 一步预测均方误差为 (13) λ=α2(n+κ)-n (14) 式中,α是很小的正数,一般取10-1≤α≤1;κ=3-n;β取值与x的分布有关,对于正态分布β=2最优。 (15) (4)量测更新 (16) (17) 滤波增益为 (18) 估计均方误差为 (19) 状态估计值为 (20) 无人机(型号U-SN05)采用捷联惯导(strap-down inertial navigation system, SINS)和合成孔径雷达(synthetic aperture radar, SAR)组合系统进行导航,系统的状态方程和观测方程如下所示[8-9]。 系统的状态方程为 (21) 式中,f(·)为非线性函数,其表达式由式(22)给出,X(t)为系统状态向量,W(t)为系统噪声。 (22) 噪声系数矩阵为 (23) 系统噪声向量W(t)为 W(t)=[WεxWεyWεzWεmxWεmyWεmz (24) 将气压高度计得到的高度信息加入到SINS/SAR组合导航系统中,得到组合导航系统的状态量为 X(t)=[δvN,δvW,δvU,δφ,δλ,δh,φN, (25) 式中,(δvN,δvW,δvU)为速度误差,(δφ,δλ,δh)表示位置误差,(φN,φW,φU)为姿态误差,(εx,εy,εz)为陀螺常值漂移,(▽X,▽Y,▽Z)为加计零偏,δhb高度计误差。 SINS/SAR组合导航系统的量测误差为 Z(t)=A(t)X(t)+e(t) (26) 因为SINS和SAR都可以输出经、纬度和航向角信息,所以,组合导航系统的量测量选为 (27) 其中 (28) (29) 式中,δpψ为SAR图像匹配输出的航向角误差,δpw和δpn分别为东向和北向位置误差,其大小依赖于所采用的图像匹配算法的精度。RM,RN分别为参考椭球子午圈和卯酉圈上各点的曲率半径。 为了测试试验型无人机(型号U-SN05)的性能,于2012-09-21在内蒙古某地进行了测试飞行。无人机采用5.1节所描述的组合系统进行导航,经过约5 min初始化后起飞,分别进行了转弯、爬升、俯冲等机动飞行动作,持续飞行约56 min后完成整个飞行过程。在无人机起飞地点约500 m处设地面观测站,观测记录无人机的实时导航信息,作为导航系统输出的参考信息。 图1 采用三种滤波算法得到的经度误差曲线 图2 采用三种滤波算法得到的纬度误差曲线 图3 采用三种滤波算法得到的高度误差曲线 计算结果如图1~图3所示。从计算结果可以看出,UKF、AUKF和SRWUKF三种算法在位置误差解算精度上滤波性能有明显差别。图1中,由UKF滤波得到的经度误差范围在(-23 m, 20 m)之间,误差均值为5.425 0 m,由AUKF滤波得到的经度误差范围在(-16 m, 15 m)之间,误差均值为4.089 6 m,而SRWUKF滤波得到的经度误差范围在(-11 m, 8 m)之间,误差均值为2.614 6 m。图2中,由UKF滤波得到的纬度误差范围在(-22 m, 16 m)之间,误差均值为4.937 1 m,由AUKF滤波得到的纬度误差范围在(-25 m, 25 m)之间,误差均值为4.066 8 m,而SRWUKF滤波得到的纬度误差范围在(-9 m, 11 m)之间,误差均值为2.629 3 m。图3中,由UKF滤波得到的高度误差范围在(-32 m, 25 m)之间,误差均值为10.458 9 m,由AUKF滤波得到的高度误差范围在(-30 m, 25 m)之间,误差均值为8.766 1 m,而SRWUKF滤波得到的高度误差范围在(-25 m, 25 m)之间,误差均值为5.091 2 m。从计算结果可以看出,AUKF算法得到的位置误差精度高于UKF算法解得的误差精度,提出的SRWUKF算法的精度明显高于UKF和AUKF这两种算法。 本文在吸收Sage-Husa滤波和无迹卡尔曼滤波优点的基础上,利用随机加权估计算法将传统的定义在线性系统上的Sage-Husa噪声估计方法推广到非线性系统中,提出一种非线性Sage-Husa随机加权无迹卡尔曼滤波算法。该方法利用Sage滤波的开窗平滑方法求得观测残差向量和新息向量的协方差阵,并用随机加权自适应因子对观测残差和预测残差进行调节,以控制预测残差和预测残差对导航精度的影响。并将提出的非线性Sage-Husa随机加权UKF算法应用到SINS/SAR组合导航系统中进行计算,结果表明提出算法的滤波精度明显优于UKF和自适应UKF算法,提高了导航系统的精度。 [1] YANG Yuan-xi, XU Tian-he.An Adaptive Kalman Filter Based on Sage Windowing Weights and Variance Components[J].The Journal of Navigation, 2003, 56(2):231-240. [2] GAO Wei-guang, YANG Yuan-xi, CUI Xian-qiang,et al.Application of Adaptive Kalman Filtering Algorithm in IMU/GPS Integrated Navigation System[J].Geo-spatial Information Science, 2007, 10(1):22-26. [3] YANG Yuan-xi, GAO Wei-guang.An Optimal Adaptive Kalman Filter[J].Journal of Geodesy, 2006, 80(4):177-183. [4] GAO She-sheng, ZHONG Yong-min, SHIRINZDEH Bijan.Random Weighting Estimation for Fusion of Multi-dimensional Position Data[J].Information Sciences, 2010, 180(4):4999-5007. [5] GAO She-sheng, GAO Yi, ZHONG Yong-min.Random Weighting Estimation Method for Dynamic Navigation Positioning[J].Chinese Journal of Aeronautic, 2011, 24(3):318-323. [6] GAO She-sheng, ZHONG Yong-min.Random Weighting Estimation of Kernel Density[J].Journal of Statistical Planning and Inference, 2010, 140(9):2403-2407. [7] GAO She-sheng, FENG Zhi-hua, ZHONG Yong-min, et al.Random Weighting Estimation of Parameters in Generalized Gaussian Distribution[J].Information Science, 2008, 178(9):2275-2281. [8] ZHONG Yong-min, GAO She-sheng, LI Wei.A Quaternion-based Method for SINS/SAR Integrated Navigation System[J].IEEE Transactions on Aerospace and Electronic Systems, 2012, 48(1):514-524. [9] GAO She-sheng, ZHONG Yong-min, ZHANG Xue-yuan,et al.Multi-sensor Optimal Data Fusion for INS/GPS/SAR Integrated Navigation System[J].Aerospace Science and Technology, 2009, 13(4-5):232-237.4 Sage-Husa随机加权UKF算法
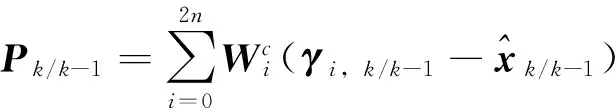

5 算例与分析
5.1 SINS/SAR组合导航系统数学模型

W▽XW▽YW▽ZWΨxWΨyWΨzWhb]T
φW,φU,εx,εy,εz,▽X,▽Y,▽Z,δhb]T5.2 计算与分析


6 结束语

