用单频GPS数据实现低轨卫星动力学法定轨研究

张德成，郑作亚，王霞迎，李 伟，3

(1.山东科技大学，山东 青岛 266590；2.中国测绘科学研究院，北京 100830；3.兰州交通大学，兰州 730070)

1 引言

目前，低轨卫星精密定轨技术已经发展的比较成熟，定轨精度可以达到厘米级水平[1-4]。在利用星载全球定位系统(global positioning system，GPS)观测数据进行定轨时，许多都是基于双频GPS观测数据解算的，基于单频观测数据的定轨研究相对较少[5]。文献[6]利用HY-2和ZY-3单频观测数据，得到的简化动力学轨道三维精度可以达到1～2 dm[6]，其中用到了半合组合观测量(group and phase ionospheric correction， GRAPHIC)消去电离层一阶项的影响，对采用单频星载GPS数据进行低轨卫星定轨具有一定参考价值。

本文通过GRACE A卫星的星载GPS观测数据，分别采用单频GRAPHIC组合观测量和双频消电离层组合观测量，运用动力学低轨卫星定轨方法进行解算，证明了利用单频观测数据(C/A和L1)进行定轨的可行性，并对定轨结果进行了精度评估。

2 定轨方法

2.1 动力学法低轨卫星定轨

动力学法是比较传统的定轨方法。基于GPS观测数据的动力学低轨卫星定轨方法原理为：首先利用加载在低轨卫星上的力学模型及描述低轨卫星的物理模型等，计算出低轨卫星的参考轨道；然后通过最小二乘方法，使动力法获得的轨道解和GPS跟踪数据达到最佳拟合，从而得到较为准确的低轨卫星轨道。

在动力学法低轨卫星定轨中，力学模型精度的高低是制约定轨精度的关键问题[7]。因此，对于高速运行的低轨卫星来说，必须分析卫星所受到的各种摄动力、精化各种力学模型，才能保证定轨的精度和可靠性。一般将低轨卫星所受摄动力分为保守力和非保守力，保守力包括地球引力摄动、潮汐摄动、N体摄动和相对论效应摄动，非保守力包括太阳光压摄动、地球反照与红外辐射压摄动和大气阻力摄动等。

卫星在地心惯性系下的运动方程和初始状态可表示为[8]

(1)

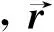
2.2 GRAPHIC观测模型

在利用GPS双频观测数据进行低轨卫星定轨解算的时候，通常采用无电离层延迟线性组合(PC/LC)的方式消除电离层误差的影响。而当利用单频数据(C/A和L1)进行解算时，通常有两种方法。一种是通过电离层模型加以改正，像全球电离层模型(global ionospheric maps，GIM)对电离层延迟改正效果可以达到90%以上[9]；另一种方法就是通过C/A码伪距和L1载波相位线性组合的方式，这一方法是由Yunck于1993年首先提出的，称为GRAPHIC观测量[10-12]。

对于码伪距和载波相位观测量，电离层延迟一阶项的影响占到整个电离层延迟的99.9%，并且大小相等，符号相反。因此，通过求码观测量和载波相位观测量的平均值，即采用GRAPHIC线性组合观测量，就可以消除大部分电离层延迟的影响。考虑到一般低轨卫星的轨道高度，不考虑对流层延迟的影响。同时，对于多路径效应、码偏差和相对论效应也不加考虑。C/A码伪距和载波相位观测方程可表示为

C=ρ+ctr-cts+Vion+εC

(2)

Φ=ρ+δtr-δts-Vion+λ1N+εΦ

(3)

式中，C和Φ分别为C/A码伪距和载波相位观测量，ρ为GPS卫星到低轨卫星接收机的几何距离，tr为接收机钟差，ts为卫星钟差，Vion为电离层延迟一阶项，λ1为L1载波相位波长，N为L1载波整周模糊度，εC和εΦ分别为C/A码伪距和L1载波相位的观测噪声,c为光速。

由此可得到GRAPHIC组合观测量方程为

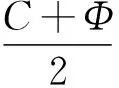
(4)

3 实验算例分析

选取2013-01-11-17GRACE A卫星的GPS跟踪数据，分别利用单频和双频观测数据，采用动力学低轨卫星定轨方法，解算了7 d的卫星轨道，并采用两种方法对定轨结果进行精度评定。

3.1 与RSO轨道进行比较

从德国地学研究中心下载了对应定轨时间段内的快速科学轨道(rapid science orbit， RSO)，以此作为参考轨道分别与两种策略定轨得到的结果进行比较。得到如下统计结果，图1和图2是分别通过GRAPHIC单频组合观测量定轨的结果和双频消电离层组合观测量定轨的结果与参考轨道比较得到的残差曲线图；图3和图4分别是对应的均方根误差和三维位置误差统计图。

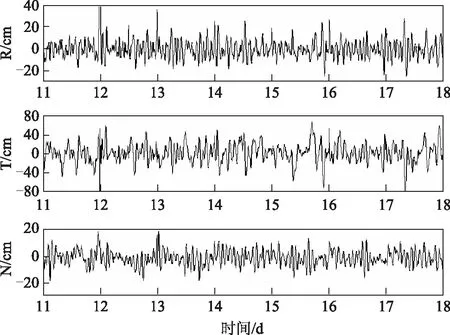
图1 GRAPHIC观测量解算轨道与RSO轨道比较残差图

图2 双频消电离层组合观测量解算轨道与RSO轨道比较残差图

图3 GRAPHIC观测量解算轨道与RSO轨道比较误差统计

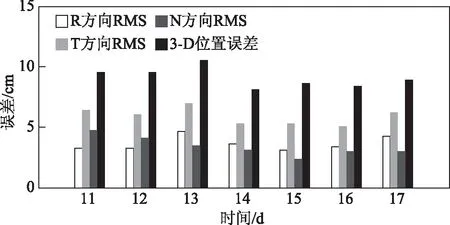
图4 双频组合观测量解算轨道与RSO轨道比较误差统计

由图1和图2可以看出，两种定轨策略得到的结果在R、T、和N方向上的残差变化均匀，无明显系统偏差，但采用GRAPHIC观测量解算的轨道与参考轨道相比较，残差较大。由图3和图4可以看出，相比双频数据，采用单频数据的定轨结果较差，这主要是因为在GRAPHIC观测量中虽然消去了电离层延迟的影响，但是码和载波相位观测噪声却依然存在。由于载波相位观测噪声相对较小，因此GRAPHIC观测量的观测噪声约为独立码观测噪声的一半，这与实际情况是相符的。与RSO轨道相比较，由单频数据和双频数据分别解算得到的定轨结果在R、T、N方向上均方根(root mean square，RMS)的平均值分别为7.9 cm、20.1 cm、5.5 cm和3.5 cm、5.8 cm、3.3 cm，三维定轨精度平均值分别为22.8 cm和9.0 cm。

需要注意的是，在进行动力学定轨时，没有考虑地球反照与红外辐射压和大气阻力这些难以模型化的摄动力的影响。在优化各种力学模型后，定轨的三维精度可以优于20 cm，能够满足一般低轨卫星定轨精度的要求。

3.2 通过卫星激光测距观测数据进行检核

通过比较卫星激光测距(satellite laser ranging，SLR)直接测得的站星距与GRACE卫星反算的站星距得到GRACE卫星的轨道检核结果，可以进一步评价卫星轨道的精度[13]。表1给出了采用SLR数据校核GRACE A卫星轨道的统计结果。图5为对应的残差分布图，其中图5(a)和图5(b)分别为双频定轨结果和单频定轨结果的残差图。

本算例采用定轨时间段内11个SLR观测站的402个地壳动态数据信息系统(crustal dynamics data information system，CDDIS)标准点数据，得到轨道检核结果。对单频GRAPGIC组合观测量定轨结果进行检核，残差平均值为-1.8 cm，均方根误差RMS为8.6 cm，标准差为13.7 cm；对采用双频消电离层组合观测量定轨结果进行检核，残差平均值为-0.7 cm，均方根误差RMS为3.3 cm，标准差为5.3 cm。可以看出，各个观测站台不存在较大系统偏差，检核结果与采用RSO比较的结果一致。

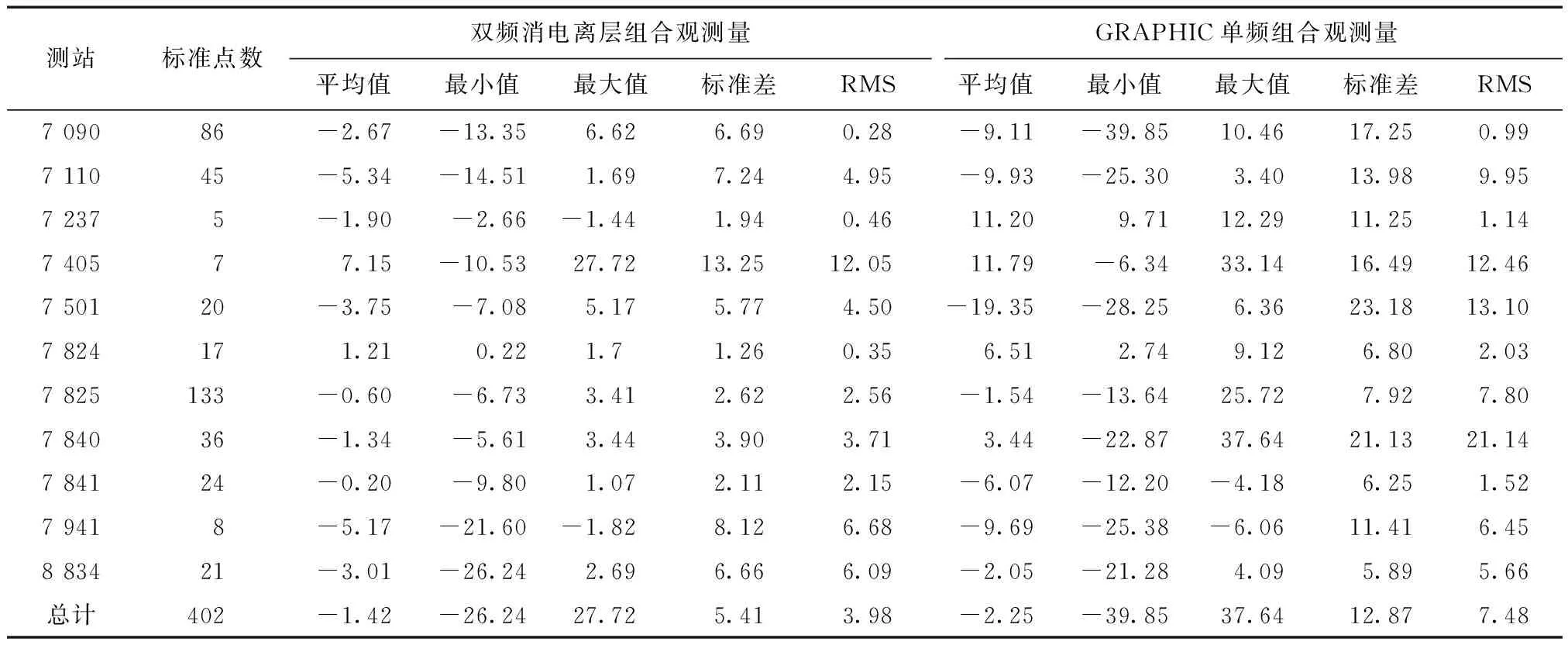
表1 SLR数据检核GRACE A卫星轨道的比较结果/cm

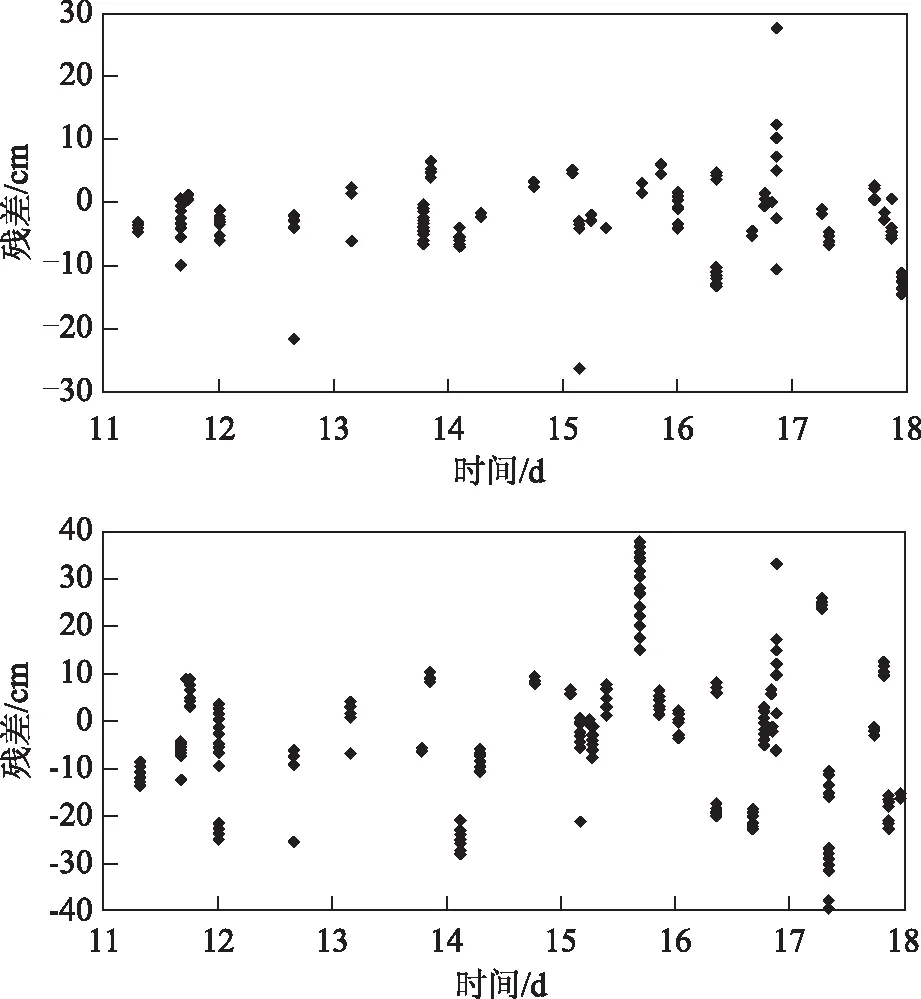
图5 GRACE A卫星站星距与SLR测距信息的残差图

4 结束语

本文基于单频GRAPHIC组合观测量和双频消电离层组合观测量，通过动力学低轨卫星定轨的方法分别进行解算，证明了运用GRAPHIC组合观测量进行动力学定轨的可行性，并且精度满足一般低轨卫星定轨的要求。这对只装载有单频接收机的低轨卫星定轨，或者对于双频接收机在非完好条件下(不能获得完好的双频观测数据)的低轨卫星定轨，都具有一定的参考价值。

[1] 赵春梅，程鹏飞，益鹏举.基于伪随机脉冲估计的简化动力学卫星定轨方法[J].宇航学报，2011(4)：762-766.

[2] 盛传贞，甘卫军，赵春梅，等.利用星载GPS数据确定厘米级Jason-1卫星精密轨道[J].测绘通报，2012(4)：11-14.

[3] 朱俊，王家松，陈建荣，等.HY-2卫星DORIS厘米级精密定轨[J].宇航学报，2013，34(2)：163-169.

[4] 韩保民.基于双频P码的星载GPS低轨卫星相对定轨研究[J].测绘通报，2005(9)：6-9.

[5] 胡国荣，欧吉坤，崔伟宏.星载单频GPS接收机低轨卫星几何法定轨研究[J].天文学报，2000，41(3)：278-288.

[6] 郭向，张强，赵齐乐，等.基于单频星载GPS数据的低轨卫星精密定轨[J].中国空间科学技术，2013(2)：41-46.

[7] 罗志才，钟波，宁津生，等.GOCE卫星轨道摄动的数值模拟与分析[J].武汉大学学报：信息科学版，2009，34(7)：757-760.

[8] 王威，于志坚.航天器轨道确定：模型与算法[M].北京：国防工业出版社，2007.

[9] 彭冬菊，吴斌.GIM在LEO卫星单频GPS定轨中的应用[J].天文学报，2012，53(1)：36-50.

[10] MONTENVRUCK O.Kinematic GPS Positioning of LEO Satellites Using Ionosphere-free Single Frequency Measurements[J].Areospace Science and Technology，2003，7(5)：396-405.

[11] BOCK H，JAGGI A，DACH R，et al.GPS Single-frequency Orbit Determination for Low Earth Orbiting Satellites[J].Advances in Space Research，2009，43(5)：783-791.

[12] 宋伟伟，施闯，姚宜斌，等.单频精密单点定位电离层改正方法和定位精度研究[J].武汉大学学报：信息科学版，2009，34(7)：778-781.

[13] 秦显平，焦文海，程芦颖，等.利用SLR检核CHAMP卫星轨道[J].武汉大学学报：信息科学版，2005，30(1)：92-95.