无穷小（大）量分析与正项级数敛散性

张现强 武同雁

（西南财经大学天府学院，四川 绵阳 621000）

0 引言

从有限到无穷是初等数学进入高等数学的一个重要标志，而要处理关于与无穷相关的问题必然离不开极限这个重要工具。极限是高等数学特别是微积分中最基本、最重要的概念之一。

在《高等数学》级数这一部分内容的学习中，极限也同样是一个非常重要的工具。首先，级数的敛散性是通过其前n项和的极限是否存在来定义的；其次，级数收敛的必要条件是通项的极限，即un是一个无穷小量；还有后面正项级数敛散性的各种判定方法也与极限有关。

这里，我们重点讨论一下正项级数的比较判别法。在教学中发现，这种方法学生掌握起来比较困难，不知如何下手去找作为参考的级数。在此，我们介绍通过无穷小（大）量分析的方法，利用阶的估计来寻找参考级数，从而判断级数的敛散性，方法简单实用。

1 一般教材中介绍的比较判别法的两种形式

简单来说就是“大的收敛，小的也收敛；小的发散，大的也发散”。这样，我们在说明一个级数un收敛时，就需要把其通项un适当放大到vn，使得级数vn是一个收敛级数；而要说明级数un发散时，就需要把其通项un适当缩小到vn，使得级数vn是一个发散级数。这时要求我们必须把握好放大或缩小的“度”，这一般来说并不容易。于是，又有了比较判别法的另一种形式：

（1）的敛散性已知；（2）的值要能确定。

针对这两个依据，我们可通过对通项un的无穷小量的阶数来分析，求取一个适当的参考级数。

2 无穷小量（或无穷大量）分析方法

2.1 分析un的分母的无穷大的阶来求取vn

当un的分子分母都为无穷大量时，通过综合分析确定un的无穷小量的阶，从而求取vn

下面举例来说明：

例1 判定下列级数的敛散性

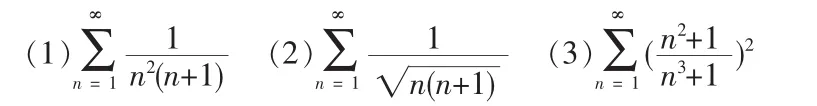
上述级数通项un的分母的无穷大的阶数分别为（1）是3阶，（2）是1阶，（3）是2阶，所求取的参考级数的通项vn分别可取，从而（1）（3）收敛，（2）发散。

命题1 指数函数ax(a＞1)是x→+∞时的无穷阶无穷大量。

证明 取n阶无穷大量xn(x→+∞)，这时有

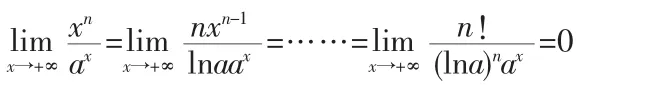
无论n为多么大的一个正数，都有上述极限成立。因此指数函数ax(a＞1)的阶比无论多么高阶的无穷大量xn的阶都还要高，是无穷阶无穷大量。

[注记] 指数函数a-x(a＞1)是x→+∞时的无穷阶无穷小量。

命题2 对数函数ln x是x→+∞时的零阶无穷大量。

更进一步，有

(ln n)k≪nα≪an≪n！ ≪nn(k,α＞0,a＞1,≪表示远远小于)

例2 判定下列级数的敛散性

（1）中由于3n是无穷阶无穷大量，无穷大阶远高于n的1阶，较3n之趋于无穷大，n可忽略不计，因此只取；级数收敛。 （2）中由于ln n是零阶无穷大量（虽是零阶，但毕竟是无穷大量！），任何α阶无穷大量nα(α＞0)的阶都比它的阶高，在此不妨考虑为，因此取vn=即可；从而此级数收敛。（3）中考虑ln n与同阶不能判别其敛散性，α必须小于，不妨考虑为，因此取，此级数收敛。

2.2 利用等价无穷小代换求取vn

利用un的等价无穷小作为vn，此时敛散性与对应一致。

参考级数的通项vn分别可取成un的等价无穷小为（1）

3 结束语

借助于极限，掌握了无穷小量阶数的分析，在利用比较判别法判定级数的敛散性时就可以很快的找到作比较的级数从而做出判断，此方法简单有效。

［1］龚德恩.经济数学基础（第一分册 微积分）[M].成都：四川人民出版社,2005.

［2］王国政,王婷.微积分（下）[M].成都：西南财经大学出版社,2009：65-69.

［3］尹逊波,杨果俅.全国大学生数学竞赛辅导教程[M].2版.哈尔滨工业大学出版社,2013：35-36.