卫星变轨时速度如何改变的定量分析*
陈 泽 陈娜娜 支启军
(贵州师范大学物理与电子科学学院,贵州贵阳 550001)
随着近几年来中国航天事业的迅速发展,特别是探月工程取得了重大的进展.中学生也对该方面的知识产生了浓厚的兴趣,而最感兴趣的多集中在“卫星变轨”问题,这正是高中物理教学中的难点,也是高考物理试题中的热点,特别是卫星变轨时,速度如何变化,更是困扰很多学生的一大难题.要解决这一问题,可以定性半定量分析;若不考虑其他因素干扰的情形(如大气阻力,其他星体的引力场,光压等的影响),也可以利用初等数学的知识进行严谨的定量分析.
1 问题的提出

2 卫星变轨时速度如何改变的定性半定量解释
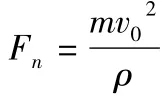
3 卫星变轨时速度如何改变的定量分析
为了定量解决这一问题,必须引入引力势能的概念.对于物体的重力势能,它是物体在空间上与地球间的相互关系而具有的能量,那种与物体间相对位置有关的能量的一般就称为势能[2].一定位置势能的大小在数值上等于从势能零点到此位置保守力做功的负值[3],因此先考虑万有引力做功的特点,以下将用微元法得出万有引力做功的表达式[4].
先计算离地心距离r1位置的卫星变轨到r1+Δr位置(如图 1 所示,Δr、Δθ取值很小),万有引力所做的功为

图1

则离地心距离r1位置的卫星变轨到r2位置,万有引力所做的功为
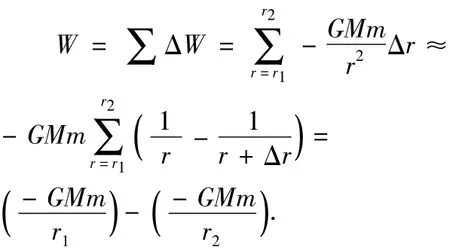
根据上面的结论可知,万有引力做功满足保守力做功的特点.因此可以引入引力势能,其大小等于从引力势能零点到此位置引力做功的负值.一般说来,引力势能零点位置取在无限远位置.则卫星离地心距离r位置时地-卫系统的引力势能EP(r)的表达式为

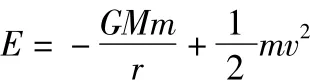
假设卫星在变轨前的速度由v1改变为v1'如图2所示,变轨过程中系统的机械能守恒,则有

图2

由(1)、(2)式得


因此v1'>v1.即要增大卫星离地心距离r1位置的速度.
同理可得,若离地心距离r2的高轨道卫星要实现向离地心距离r1的低轨道变轨,则v2'<v2.即要减小卫星离地心距离r2位置的速度.
1 雷航英.巧用曲率半径突破卫星变轨教学之难度[J].物理教师,2013(7):57.
2 R.P.Feynman等著,郑永令等译.费恩曼物理学讲义(第1卷)[M].上海:上海科学技术出版社,2005:36.
3 漆安慎,杜婵英.普通物理学教程.力学[M].北京:高等教育出版社,1997:123.
4 程稼夫.中学奥林匹克竞赛物理讲座[M].合肥:中国科学技术大学出版社,2000:139.
——《势能》