溶液吸附法测定硅胶表面分形值

邱 诚*，李 玫

(1成都工业学院 机电工程系，成都 611730;2成都学院 城乡建设学院，成都 610106)

在欧几里德几何学中，用整数描述几何形体:点为0维，线为一维，面为二维，体为三维。整数维利于抽象思维，但与实际情况往往有偏差。绝对平整的几何平面为二维，客观世界中的“平面”并不完全平整。自然界中存在的各种复杂形态的物体用整数维表示就过于简单。

20世纪70年代，法国数学家Mandelbrot创立分形几何学［1］。分形理论认为维数也可以是分数，为了精确定量地描述客观事物的“非规则”程度，将维数从整数扩大到分数，从而突破了一般拓扑集维数为整数的界限。分形几何学认为空间物体的维数可以连续变化，即1～3的分数值，称为分形值。分形值越大，表面越粗糙，充满空间的程度越大［2-5］。因而对于固体，表面的分形值可表征粗糙程度。另外，吸附热力学参数，如ΔH，ΔS和ΔG与分形值有直接关系［6］。

对于污水中色度、重金属等污染物的去除，吸附剂的吸附能力尤为重要。一般地，分形值大的物体因表面较粗糙，在同等条件下体现出较强的吸附能力。本文利用溶液吸附法，测得不同吸附质溶液在吸附平衡时的特征数据，利用平衡吸附量与分形值之间的重要关系nm∝r-D，求得分形值的大小。

1 实验方法与原理

测定分形值的方法有物理法和化学法。化学法所需实验条件较简单，易操作。其中，吸附法具有方便、快速的特点，是测定分形值的典型方法之一。本研究采用液相吸附法测定分形值，其原理是:在一定温度下，吸附质在1g固体表面形成单分子层覆盖，若测出单层平衡吸附量，并计算出吸附分子的平均横截面积，则可根据相应结果求得吸附剂表面分形值。

D.Avnir等［7-8］用烷烃吸附测出八面沸石的D值为1.96;孔性硅胶、粒状活性炭等的D值为2.7～2.9，无孔氧化硅、炭黑、活化无孔炭等的 D值为1.9 ～2.1。赵振国等［9］利用 Langmuir方程直线式可求出硅胶自CCl4稀溶液中吸附脂肪醇的极限吸附量nl，再根据硅胶比表面积值(417 m2/g)计算出极限吸附时每个分子所占的表观面积σa。本研究直接利用平衡吸附量nm取代极限吸附量nl，求得硅胶表面D值。

取0.2%的吸附质溶液50 mL，加入硅胶吸附剂500 mg，在恒温振荡器中匀速震荡2 h，吸附平衡后，取上层清液，测其吸光度。根据吸附质溶液的A-C标线，计算吸附平衡溶液的浓度值C＇，从而得到不同吸附质的平衡吸附量nm。

设吸附质分子的截面半径为r，在完全平整的表面上，1g吸附剂的单分子层平衡吸附量nm正比于比表面积A，即 nm∝A。显然，A∝r2nm。当吸附剂一定，即A确定时，nm∝r-2。当吸附剂是分形值为D的粗糙表面时，则有:nm∝r-D。取对数后得到:lg nm=-Dlg r+k，其中，k为常数。设吸附质分子的平均截面积为σ，则，即

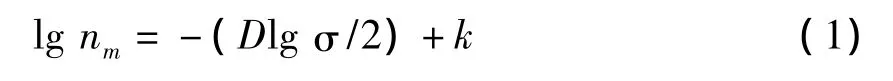
σ可根据A和nm计算:σ=A/(nmNA)，其中:NA为阿怫加德罗常数(Avogadro constant)。将nm与σ值代入式(1)中，即得D值。

2 实验材料与仪器

实验材料选用市售比表面积400 m2/g，平均孔径60 nm硅胶作为吸附剂;亚甲基蓝、结晶紫、番红花红T、酸性红94和甲酚红等5种染料作为吸附质。

实验仪器为721型紫外-可见分光光度计，恒温振荡器。

3 实验结果

3.1 吸附质溶液标准曲线

配得不同浓度的吸附质溶液，测定其在特征波长下的吸光度A，建立5种吸附质溶液A-C标线，如图1所示。

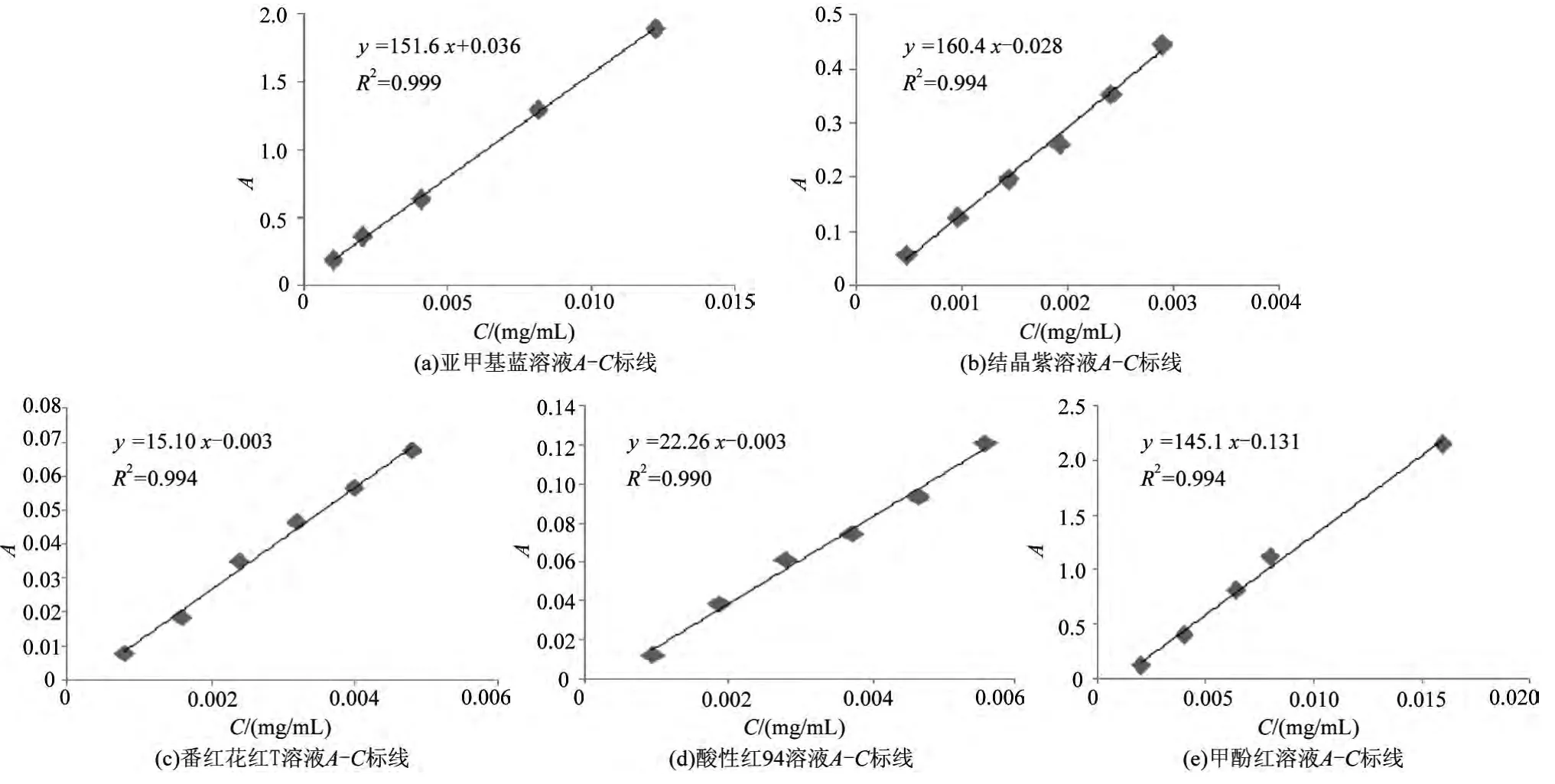
图1 吸附质溶液A-C标线

3.2 吸附质溶液的平衡吸附量

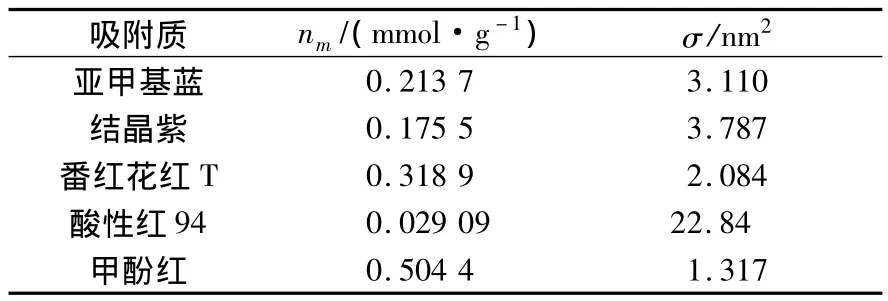
表1 硅胶自水溶液中吸附不同吸附质的nm和σ值

表1列出了一种硅胶自水溶液中吸附染料吸附质的结果，图2为该体系的lg nm-lg σ图。根据图2中直线的斜率和式(1)求出该硅胶表面的分形值D为2.002。该值与硅胶(417 m2/g)通过气体吸附和脂肪醇液相吸附法所测结果接近［10］。

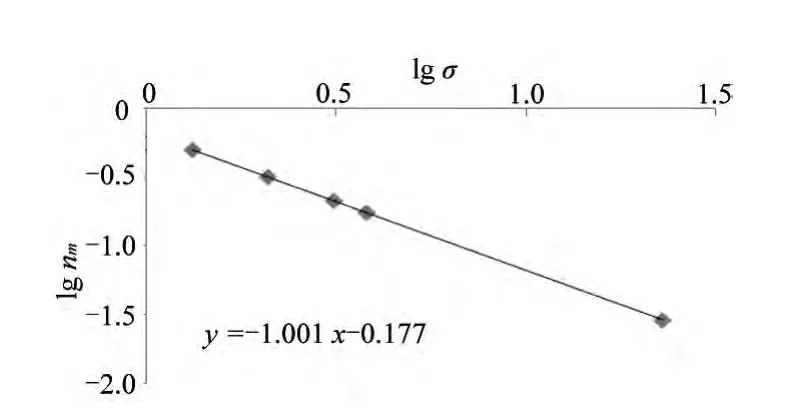
图2 硅胶自水溶液中吸附不同吸附质的lg nm-lg σ图

4 分析与讨论

1)中孔硅胶表面D值的大小，与固体表面的均匀性、连续性有关，同时也受局部曲率半径大小影响。实验结果表明:中孔硅胶表面D值较小，硅胶表面均匀，连续性好，并且硅胶固体表面各局部的曲率半径相较吸附质分子半径较大，表现出低分形值的特点。

2)根据溶液中吸附结果计算分维D值鲜有报道。原因在于，溶剂吸附现象的存在，导致实验结果存在明显偏差。硅胶吸附剂自水溶液中进行溶质吸附的实验，方法简单，发生多层吸附的可能性小，并且稀溶液体系所产生的溶剂吸附的影响程度有限［11］，实验误差较小。

3)D值的计算以采用极限吸附量间接求得［3］，而极限吸附量的计算过程较为繁琐，且容易出现误差。直接利用平衡吸附量nm取代极限吸附量nl，求得硅胶表面D值，不需要利用Langmuir吸附等温线处理得到极限吸附量，计算过程更加简明，避免出现演算过程的误差。

［1］MANDELBROT B.Fractal:Form，Chance and Dimension［M］.San Francisco:Freeman，1977.

［2］王毅力，刘杰，石宝友，等.颗粒活性炭吸附染料时的表面分形分析［J］.安全与环境学报，2006(3):92-95.

［3］赵振国.用吸附数据对硅胶表面的分形分析［J］.高等学校化学学报，2003，24(11):2051-2055.

［4］陶春辉.分形几何在海底火山地形中的应用［J］.东海海洋，2000(6):9-14.

［5］胡晓梅.分形与分维简介［J］.咸宁学院学报，2006(6):25-26.

［6］JARONIEC M，LU X，Madey R，Avnir D.Fractal surface analysis by using nitrogen adsorption data:the case of the capillary condensation regime［J］.J Chem.Phys.，1990(92):7589.

［7］AVNIR D，FARIN D，PFEIFER P.Molecular fractal surfaces［J］.Nature.，1984(308):261-263.

［8］AVNIR D，FARIN D，PFEIFER P.Chemistry in noninteger dimensionsbetween two and three. II. Fractalsurfacesof adsorbents［J］.J.Chem.Phys.，1983(79):3566-3571.

［9］赵振国，顾惕人.自溶液中的吸附:Ⅵ.硅胶自四氯化碳中同时吸附多种脂肪醇的研究［J］.化学学报，1981，39(6):503-511.

［10］赵振国.吸附作用应用原理［M］.北京:化学工业出版社，2005.

［11］刘阳桥，高濂，郭景坤.高价小分子型分散剂在Al2O3表面的吸附研究［J］.高等学校化学学报，2001，22(3):435-438.