基于圆故障模型的模拟电路故障诊断方法

熊 建*

(成都工业学院 通信工程系，成都 611730)

作为电子系统中重要的组成部分，模拟电路由于自身的特性［1］，如在时域和频域响应信号的连续变化性、元件容差问题、复杂结构等原因，缺乏实际可靠的故障模型及诊断方法，使得模拟电路部分的故障诊断成为电子系统故障诊断的瓶颈，制约着电子系统故障诊断领域的发展。20世纪70年代以来，模拟电路故障诊断取得了一定的进展，一些故障模型和诊断方法被提出［1-12］，其中被广泛利用并具有实际应用价值的是故障字典法［3-12］。由于模拟电路中元件参数值变化是连续的和不可数的，不同的参数导致不同的响应，所以通过传统的故障字典法选取有限的响应特征和对应故障形成的字典不能完全覆盖所有的电路状态，即字典中没有建模的故障参数所对应的故障不能被有效地诊断。要提高诊断准确性，就必须对故障元件的各种连续变化参数值进行完备的故障仿真来建立字典，这必然造成字典规模庞大和效率低下。同时，容差问题对故障诊断的影响也一直困扰软故障诊断。因此寻找一种合适的软故障模型是当前学术界研究热点。

为此，本文在复平面故障模型［11］的基础上，提出一种圆故障模型的诊断方法。该方法放弃了传统采用少数几个固定参数建立故障字典的方式，而采用圆方程作为特征模型建立字典，能解决任何元件参数变化的故障诊断(软硬故障)和容差问题。

1 圆故障模型原理

图1 测试电路

设测试电路N是一线性时不变电路(如图1(a)所示)，使用独立电压源作为输入信号为输出电压。x为某无源元件(电阻、电导、电感、电容等)，电压为。根据替代原理，在电路中，x可用电压值为的独立电压源替代，如图1(b)所示。由戴维南定理可得:

其中:H＇(jω)，H"(jω)分别是独立源工作时电路的传送函数。因此，由叠加原理可得:

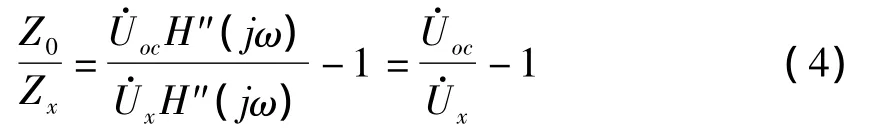
图2 实验电路

由式(5)可知，在复数域上，R0、X0、a、b 与元件x的参数无关，仅取决于电路的拓扑结构和其他无故障元件参数。式(5)可以作为故障模型，但在实际模拟故障诊断中，用式(5)不便建立故障字典。把(5)式两边同时乘上变换，整理得:

可看出式(6)为圆一般方程，其中:x为Uor;y为Uoj;系数 D，E，F 分别为 bR0/X0-a，aR0/X0+b，0。系数D，E，F对于某一元件来说是固定值，是由于R0，X0，a，b仅仅与其位置及电路拓扑结构有关，与故障元件参数无关。而输出电压值与故障元件的参数是相关的，并且故障元件参数变化引起的输出电压值在复平面都满足一独立的圆方程。因此可以用式(6)作为故障模型。圆方程作为故障特征能替代大量的仿真数据，减少字典规模和降低测试时间代价。

2 故障诊断方法及相关问题

2.1 故障字典的建立

故障模型字典建立仿真步骤为:1)采用Monte-Carlo分析方法仿真电路在各元件具有容差条件下正常输出电压变化范围，以便建立无故障圆范围。2)获取在标称值状态下测试点电压值。3)仿真各元件在开路，短路状态下测试点的电压值。4)通过编程，利用以上3个特殊参数值，计算出标准圆方程及圆心坐标和半径R。5)根据1)～3)步内容，给出无故障圆方程和故障圆方程，完成字典的建立。

2.2 测后故障诊断

获得电路中测试点的多个实际电压值(复数形式)后，再经2个步骤可以确定电路的状态和定位故障。

第1步:故障的诊断。通过确定测试点值是否在无故障圆范围内，判断电路是处于正常状态还是处于某一可测故障状态。

第2步:故障的定位。通过欧式距离法，计算实测值到每个圆中心的距离。若与该圆的半径相等或相近(实测值可能受到其测试环境影响如干扰等，而造成距离不完全相等)，则故障属于该圆所对应的故障模型，因此该故障被精确定位。

3 电路故障诊断实例及分析

图2为标准被测电路Two-Thomas filter的原理图，其中:Ri=10 kΩ(i=1，2，3，4，5，6)，C1=C2=0.01 μF，其容差分别为 5% 和 10%;激励信号为幅度A=1 V，频率f=1 kHz的正弦信号;t6选定为测试节点。利用 PSpice和 Matlab仿真工具，在Window XP系统下对被测电路进行仿真。根据上述诊断方法对该电路的8种故障状态分别进行仿真。首先在容差情况下采用Monte-Carlo分析方法获取无故障圆范围，然后通过仿真获得各元件在3个特殊点的电压值，并计算圆方程的中心坐标值和半径值，最后建立故障模型字典，如表1所示。

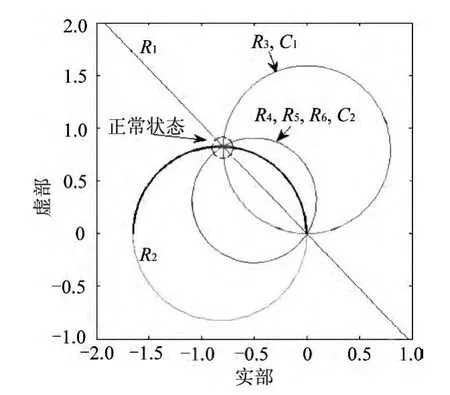
图3 Two-Thomas filter电路的故障特征曲线

图4 R2故障诊断结果示图

表1 Two Thomas滤波器故障类型及圆坐标

根据表1在复平面空间构建各故障特征曲线图，如图3所示，所有元件在容差范围内时，电路输出响应在以点(-0.80，0.83)为圆心、半径为0.003的一圆范围内随机移动。此范围内的状态称之为无故障状态，该圆为无故障圆。其他范围为故障诊断确认范围(如R2中黑色线段范围)，它包含了任何的软故障和硬故障，因此能很好地解决容差问题。其中有一些元件圆方程基本一致难以区分，如R4、R5、R6、C2，可采用增加测点的选择来进一步区分。

考察实际被测电路，将R2替换为5 kΩ，由于故障元件也含有容差情况，因此再加上±10%的容差。为真实模拟实际测试中外部的干扰，再加上随机扰动e，设置5个测试点来模拟实际电路中R2发生的故障。在测点t6的测量数据为V1(-0.3111+0.6459j)，V2(-0.3191+0.6522j)，V3(-0.2622+0.6037j)，V4(-0.2672+0.6084j)，V5(-0.3563+0.6796j)。如图4所示，虚圆中是实测值在故障特征曲线图中的位置。通过上述诊断方法，分别求其到各圆中心坐标的距离。表2为5个测试值到每个圆中心的距离，从中可以看出F2对应的5个距离都相等，因此R2能被正确地诊断出。

表2 实测值到各圆故障模型中心坐标的距离

4 结语

一个适合的模拟电路故障模型的建立在模拟故障诊断中十分关键。通过理论论证和实验验证，本文提出的圆故障模型和模拟电路故障诊断方法能很好地解决硬故障和软故障的诊断及容差影响问题。同时，采用圆方程作为故障特征，不但能解决以往对没有建模型的故障不能诊断的问题，而且能够降低字典的规模，提高诊断的可测试性。

［1］TADEUSIEWICZ M，HALGAS S，KORZYBSKI M.An algorithm for soft-fualt diagnosis of linear and nolinear circuits［J］. IEEE Transaction on Circuits and System-I:Fundamental Theory and Applications，2002，49(11):1648-1653.

［2］杨士元，胡梅，王红.模拟电路软故障诊断的研究［J］.微电子学与计算机，2008，25(1):1-8.

［3］PENG S C，WANG X F.Research on fault diagnosis of mixed-signal circuits based on genetic algorithms［J］.International Conference on Computer Science and Electronics Engineering(ICCSEE)，2012，vol.3:12-15.

［4］DENG Y，SHI Y B，ZHANG W.An approach to locate parametric faults in nonlinear analog Circuits［J］.IEEE Transactions on Instrumentation ＆ measurement，2012，61(2):358-367.

［5］SARATHI V A S，LONG B，Pecht M.Diagnostics and prognostics method for analog electronic circuits［J］.IEEE Transactions on Industrial Electronics，2013，60:1-14.

［6］LI X，ZHANG Y，WANG S J，et al.Analog circuits fault diagnosis by GA-RBF neuralnetwork and virtualinstruments［C］//2012 International Symposium on Instrumentation ＆ Measurement，Sensor Network and Automation(IMSNA)，2012:236-239.

［7］SHEN M，PENG M F，HE J B，et al.Probabilistic neural network based tolerance-circuit diagnosis［C］//7th International Conference on Computer Science＆ Education(ICCSE)，2012:13-16.

［8］YILMAZ E，MEIXNER A，OZEV S.An industrial case study of analog fault modeling［C］//IEEE 29th VLSI Test Symposium(VTS)，2011:178-183.

［9］WANG P，YANG S Y.A new diagnosis approach for handling tolerance in analog and mixed-signal circuits by using fuzzy math［J］.IEEE Transactions on Circuits and Systems-I:Regular Papers，2005，52:2118-2127.

［10］YANG C L，TIAN S L.Methods of handling the tolerance and test-point selection problem for analog-circuit fault diagnosis［J］.IEEE Transactions On instrumentation and measurement，2011，60(1):176-185.

［11］YANG C L，TIAN S L，LIU Z，et al.Fault modeling on complex plane and tolerance handling methods for analog circuits［J］.IEEE Transactions on Instrumentation and Measurement，2013，62(10):2730-2738.

［12］LONG B，XIAN W M，LI M，et al.Improved diagnostics for the incipient faults in analog circuits using LSSVM based on PSO algorithm wih Mahalanobis distance［J］.Neurocomputing，2014(133):237-248.