盾构隧道近距离正交下穿复杂地下结构的影响分析

方晓慧，王星华

(中南大学土木工程学院，湖南长沙410075)

近年来，随着我国城市地铁建设的不断发展，城市地下空间开发利用规模也在不断扩大。然而，错综复杂的地下结构却易导致盾构隧道施工遭遇与既有建(构)筑物的近接施工问题，给施工带来了极大困难。盾构隧道下穿施工引起的地层效应和结构的力学行为十分复杂，故为保证既有结构的安全及正常运营，深入研究新建隧道下穿既有结构的影响机理及控制措施显得尤为重要。

目前，研究盾构近接施工主要通过理论分析，数值模拟，模型试验及现场监测等手段，集中研究对地表沉降预测［1－4］，上覆既有隧道［5－6］，地表建筑物［7］，地下管线［8］和桩基［9］等的影响。Peck［2］提出地表沉降槽似正态分布以及地层损失的概念;刘宝琛等［4］将随机介质理论应用于浅埋隧道开挖引起的地表移动和变形预测;Imamura［5］采用离心模型试验研究在不同的隧道埋深条件和有盾尾间隙情况下衬砌拱顶土压力及地面的沉降情况，得到地表中心沉降与埋深之比的关系符合指数函数关系;张志强等［5］采用室内相似模型试验和数值模拟相结合的手段对盾构隧道正交下穿施工进行研究，得到不同工况下变形和附加内力分布变化规律;姜忻良等［7］将建筑物和开洞地基看作一个有机的整体，按照结构－土体－隧道共同作用机理，分析了地铁隧道施工对邻近建筑物的影响。但对同时下穿既有隧道及地下街此类复杂地下结构的情况研究较少，尤其是在超近距离下穿越的案例分析。本文中地铁隧道与营盘路隧道的垂直净距只有1．23 m，地下街与既有隧道的垂直净距也仅为2 m。结合长沙地铁1号线营盘路—五一广场区间实例，采用三维差分方法，对盾构隧道下穿过程进行模拟，得到不同顶推力下对既有结构的影响范围及内力、变形规律，为类似盾构隧道近接施工问题提供一定参考。

1 工程概况

长沙地铁1号线营盘路—五一广场区间线路出营盘路站后，下穿营盘路过江隧道，向南沿黄兴北路(金满地地下商业街)至中山亭，然后继续沿黄兴北路向南至五一广场站。区间下穿营盘路过江隧道，地铁隧道与营盘路隧道的垂直净距仅有1．23 m，同时下穿金满地地下商业街F区，该商业街采用伐板基础，其结构外缘净距最小8 m，地下街与既有隧道的垂直净距也仅有2 m，与地铁线路走向基本平行，依次往下分别是金满地地下商业街，营盘路隧道和地铁隧道，具体位置见图1所示。

根据工程地质描述，区间隧道主要穿越地层为强风化砂砾岩，中风化砂砾岩和粉质黏土，盾构施工时易使盾构土体产生胶结，致使刀盘变形或刀口扭曲变形、折断。隧道顶端存在残积粉质黏土和卵石层，易发生崩塌。从整体上看，本区间地质构造相对简单，无明显不良地层，具体的岩土物理力学参数如表1所示。

FLAC3D有限差分法由于具有能够适应复杂边界，非均质，非线性本构模型和分析结果全面详细等优点，被广泛运用于盾构隧道施工环境影响的模拟中。对既有隧道和地下商业街的影响控制在合理范围是隧道能否成功穿越的关键，为模拟盾构推进对2者的影响，本文采用FLAC3D进行三维数值模拟研究。

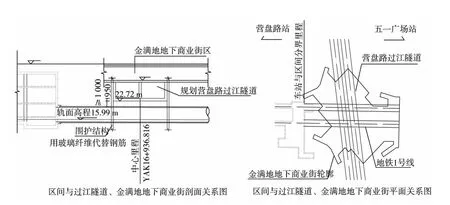
图1 交叠区域几何关系图Fig．1 The geometric relationship of the overlapping area

表1 岩土物理力学参数Table 1 Physico－mechanical parameters of surrounding rocks

2 计算模型

2．1 模型

本计算模型尺寸为84 m×62 m×49．5 m，其中X方向为84 m，Y方向为62 m，Z方向为49．5 m，模型共计22 280个实体单元，共23 536个结点。其中，金满地地下商业街埋深为3．5 m，宽29 m，长609 m，为一层地下商业街;营盘路隧道埋深为11 m，中心线位置为Z=0 m，左右线净距为7 m，其隧道直径按等效面积取直径D=10 m。地铁隧道埋深为24．2 m，中心线位置为Z=－9．7 m，左右线净距为12 m(2倍洞径D)，隧道管片衬砌的外径取D=6 m。位移边界条件选取如下:地表为自由表面，前、后、左、右四表面分别施加法向约束，模型的底面施加X，Y和Z 3个方向的约束，计算模型如下图2所示。

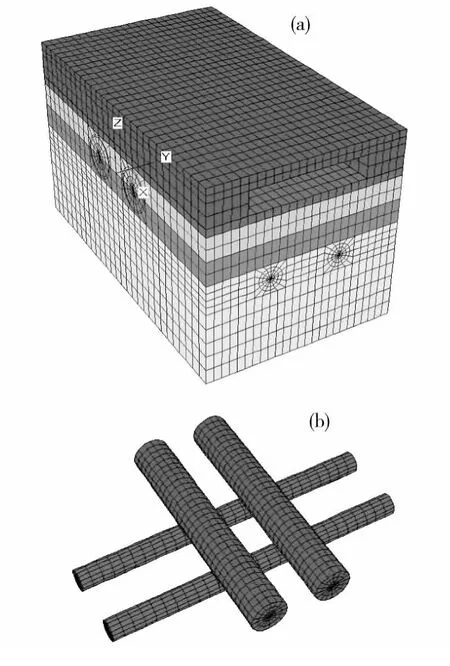
图2 三维计算模型Fig．2 3D finite element model

2．2 材料参数

土层材料采用Mohr－Coulomb模型计算，考虑材料的大变形行为，结构单元采用线弹性本构关系。其中，金满地地下商业街主体结构采用壳单元，柱网采用梁单元模拟，上下顶板厚度取0．8 m，柱网间距6 m×4 m。营盘路隧道主体结构采用30 cm厚的C30喷射混凝土，施加L=2 m的Φ25中空注浆锚杆，间距50 cm×75 cm(纵向)梅花形布置，衬砌结构采用壳单元，锚杆采用锚索结构单元进行模拟;盾构隧道管片采用C50防水混凝土，厚度0．3 m，采用壳单元进行模拟，注浆材料利用实体单元模拟。考虑到管片接缝处对强度的影响，为方便起见，对管片的整体刚度进行折减，根据错缝拼装试验的结果，将折减系数定为 0．75［1］，具体参数如表2所示。

2．3 掘进过程模拟

在盾构施工之前，首先对金满地地下商业街采用全断面一次性开挖模拟，修筑主体结构，并添加柱网结构，设置柱体与上下底板刚接，使2者能协调变形。营盘路隧道亦采用全断面一次性开挖模拟，修筑衬砌，施加锚杆。在上述2层修筑完毕后，需将位移场清零。对于地铁隧道，本文模拟的是土压平衡盾构法施工过程。其中左线盾构比右线盾构先进场，左线隧道掘进过程分为9步，其中，第1到3步每步掘进12 m(实际掘进过程中，开挖进尺一般仅为1．2 m左右，为提高计算效率，本文采用的进尺较实际情况大);第4到6步，掘削面位于既有隧道正下方，为减小开挖影响，每次掘进进尺为5 m;第7步到第9步仍一次掘进12 m;右线掘进过程与左线类似，总计经18个开挖步，双线开挖完成。

为了使模拟结果更加贴近实际，本计算严格按照实际施工步骤:(1)开挖一个掘进步长度;(2)释放土体原始应力;(3)及时安装管片;(4)施加顶推力;(5)同步注浆随着盾构推进，脱出盾尾的管片与土体间出现“建筑空隙”，该空隙用浆液通过设在盾尾的压浆管予以充填。注浆压力取1．1～1．2倍静止水压力，约0．3 MPa。在注浆单元体外围结点上施加远离盾构中心方向的注浆压力，并改变注浆体材料的属性;6)继续进行下一步开挖直至计算结束。本文考虑依次施加顶推力为168，224及335 kPa这3种情况下盾构隧道的整个掘进过程。

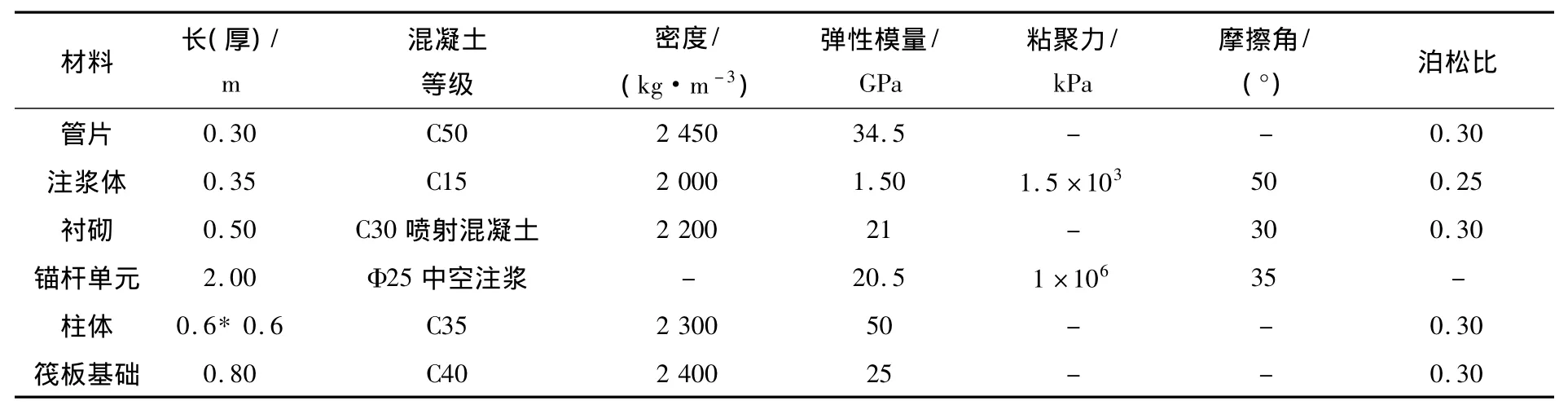
表2 材料参数Table 2 Material parameters

3 计算结果分析

3．1 地表沉降分析

盾构隧道的施工，使得隧道的下部的土体应力释放，造成一定的地层损失，从而导致地表发生不均匀沉降。

图3表示开挖完成后地表沿水平方向的沉降曲线，可以看到在开挖过程中，地表沿水平方向整体发生沉降，最大沉降量约为1．8 mm。由于地下室顶板的存在(范围从x=－21 m至x=42 m)，限制了土体的自由下沉，沉降值较其他位置有明显减小。

在3种顶推力情况下，地表的沉降变化趋势整体保持一致。在顶推力335 kPa下，地表位移的变化趋势最为显著，这是由于顶推力值增大加剧了对前方土体的扰动，结果表明顶推力大小对地表沉降有一定贡献。

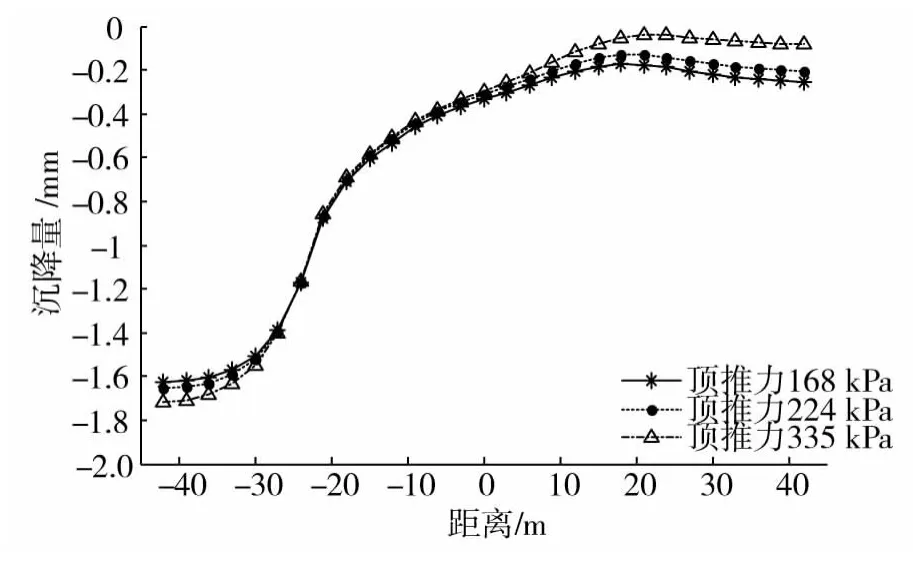
图3 地表沿水平方向沉降曲线Fig．3 Settlement curve of the ground surface along the horizontal direction

3．2 对地下商业街的影响分析

图4表示3种不同顶推力情况下，新建隧道修筑完成之后，地下街顶板沿纵向沉降曲线。从图4可以看出:竖向位移沿对称面位置向两侧逐渐减小，沉降最大值发生在对称面位置处，其值为3．5 mm。这是由于两侧端墙的刚度较大，其约束作用导致沉降主要发生在中间位置，而两端点处则较小。随着顶推力的增大，地下室顶的竖向位移呈现增大趋势。当顶推力从168 kPa增大至335 kPa，顶板的竖向位移最大值相应地从－2．93 mm增加至－3．61 mm，增大幅度达19%。结果表明，顶推力的增大加剧了对地下室上下底板的扰动，产生较大的竖向变形。

图4 地下街顶板沿纵向的沉降曲线Fig．4 Settlement curve of the longitudinal nodes at the roof of underground street

3．3 对既有隧道沉降分析

图5表示既有左隧道衬砌位移随掘进步数的变化趋势，以拱顶为例，在前3个开挖步内，即距新建隧道的掌子面前方1D～2D范围内，由于正面顶推力的存在，掌子面前方的土体表现为隆起，最大隆起量0．4 cm。从第4个开挖步起，盾构机逐步穿越整个上覆隧道，故既有隧道的拱顶位移开始表现为下沉;掘进过程中，拱顶最大沉降出现在第8步，其值为0．93 cm;继续开挖右线，既有隧道沉降有所反弹并趋于稳定，拱顶最终沉降为0．8 cm。结果表明距盾构机掌子面前方1D～2D范围内，既有隧道开始受到开挖影响;当盾构机掌子面处于其正下方时，其受到的影响最大;随着盾尾脱出，开挖影响逐步消散。随顶推力增大，拱顶位移值有所增加，与地表沉降的变化趋势保持一致。

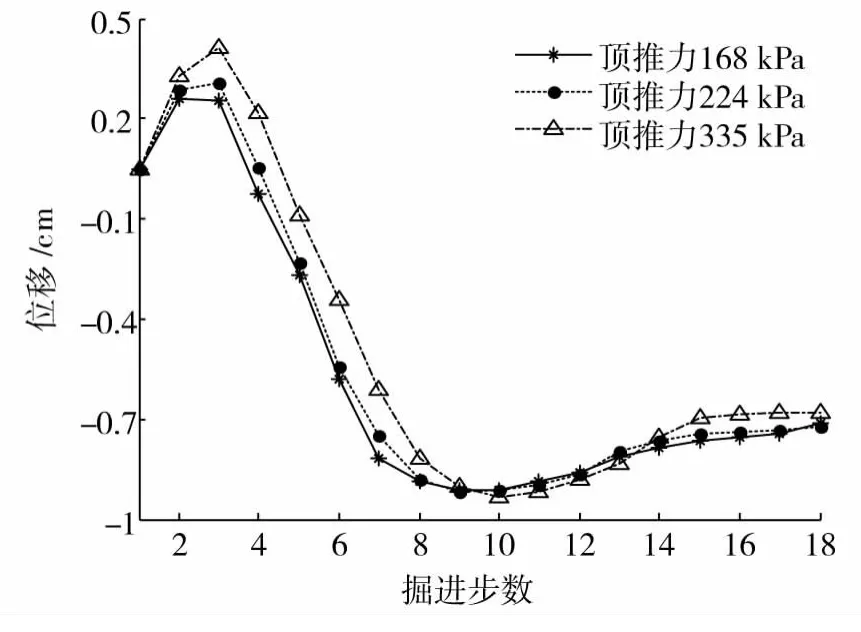
图5 既有隧道拱顶位移随掘进步变化曲线Fig．5 Settlement curve of the top of existed tunnel with excavation steps of subway tunnel

图6表示顶推力168 kPa情况下，左线、右线依次开挖完成后，沿既有隧道轴向沉降曲线，以拱顶为例，仅开挖左线(其中心线位于y=34 m处)时，既有隧道的拱顶在y=34 m处有明显沉降，最大沉降量为0．61 cm，其两侧受到周围的土体挤压有一定程度的隆起，最大隆起量0．49 cm。继续开挖右线(其中心线位于y=16 m处)，既有隧道的沉降在y=16 m和y=34 m处存在2个极值，拱顶的最大沉降发生在右线中心线对应位置即y=34 m处，其值分别为0．7 cm。结果表明第2条隧道开挖引起的沉降要略大于第1条隧道。群洞效应［10］认为第一条隧道上方土体己扰动，2洞室的变形因相邻洞室施工而相互影响叠加，当2条隧道间距较近时，沉降的叠加效应明显。总的来说，盾构的施工对拱顶的影响较大，最大沉降发生在2个新建隧道的中心线位置处。

4 对内力影响分析

4．1 对地下商业街的弯矩影响分析

图6 沿既有隧道纵向的拱顶位移曲线Fig．6 Settlement curve of the longitudinal nodes at the top of the existed tunnel

图7和图8表示地下商业街同一断面顶、底板2个结点在开挖进程中的弯矩变化情况，其中第0步表示未开挖之前的原始状态。以顶推力168 kPa为例，盾构推进导致顶板产生最大附加正弯矩值14．8 kN·m，底板附加负弯矩5．5 kN·m。自第2步起，顶板弯矩值迅速增大并于第6步达到峰值，从第7步即左线穿越建筑物后，弯矩值逐渐回落，直至第13步，弯矩值又开始增大最终趋于收敛，但峰值较左线隧道开挖时已有所降低。底板的变化规律与顶板基本保持一致，但其随盾构掘进而发生的起伏变化较顶板更为明显。由图可知:盾构机正面推力的存在，导致地下商业街处于顶板受拉、底板受压的状态。盾构推进时，顶推力的作用对地下街的影响类似于加载作用;当盾构机接近地下街时，地层损失作用更为明显，对地下街起到卸载的作用;随着盾构机的远离，这种卸载作用减弱，地下街结构内力又逐渐恢复。加大顶推力，顶板的最大附加弯矩较168 kPa情况下依次增加了0．59，1．17 kN·m，增加幅度仅为4%和7．9%。可见，随着顶推力增大弯矩值呈现增大趋势，但顶推力引起地下商业街的弯矩间的差异并不大。

图7 地下商业街顶板的弯矩变化曲线Fig．7 Moment curve of the top of the commercial street with excavation steps of subway tunnel

图8 地下商业街底板的弯矩变化曲线Fig．8 Moment curve of the bottom of the commercial street with excavation steps of subway tunnel

4．2 对既有隧道的弯矩影响分析

图9和图10表示既有隧道同一断面中拱顶和拱底2个节点在开挖进程中的弯矩变化情况，其中第0步表示未开挖之前的原始状态。既有隧道的弯矩变化规律与地下街的情况类似，以拱顶弯矩为例。自第1个掘进步起，弯矩值逐渐增大，在第5步时达到峰值，自第6步后，弯矩值开始减小，在第10步时出现反弯点，弯矩呈现出增大趋势，直至第13步后再次回落并趋于稳定。

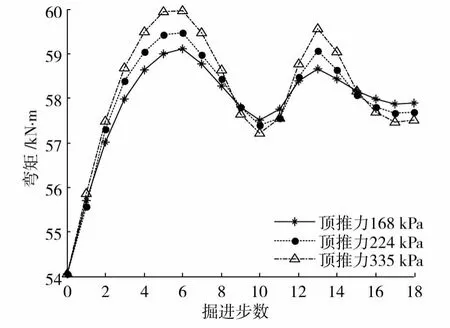
图9 既有隧道拱顶的弯矩变化曲线Fig．9 Moment curve of the top of the constructed tunnel with excavation steps of subway tunnel

图10 既有隧道拱底的弯矩变化曲线Fig．10 Moment curve of the bottom of the constructed tunnel with excavation steps of subway tunnel

对于圆形衬砌而言，其理想的受力状态为均匀受压状态，此时结构较为稳定。盾构推进引起了较大的附加弯矩，使得既有隧道处于拱顶受拉、拱底受压的不利的受力状态。在前后2次穿越既有隧道过程中，弯矩两次峰值均出现在盾构机下穿既有隧道正下方交叠区域时，由于盾构左右线之间存在2D间距，故右线开挖引起的弯矩峰值较左线已有所减小。以168 kPa情况为例，拱顶、底的弯矩右线开挖时较左线减小了0．446 kN·m和1．426 kN·m。

在3种不同顶推力下，既有隧道弯矩变化规律与地下街相似，随着顶推力增大，拱顶附加弯矩最值较168 kPa时依次增加了5．9%和14．2%，拱底依次增加了6．3%和12．4%。可见，顶推力的大小对既有隧道内力的影响要甚于地下街。

4．3 对轴力的影响分析

表3表示顶推力168 kPa下，既有隧道同一断面的拱顶、底和两侧拱腰及该断面正上方的顶、底板共6个节点的轴力变化情况。拱顶，拱底顶板和底板4个节点处的轴力随开挖大致呈现出先增大后减小，再增大又减小的趋势，而隧道两侧拱腰处轴力值变化幅度很小，无明显的变化规律。拱顶、底处最大附加轴力为－5．4和－6．26 kN，顶、底板处附加轴力为3．06和－5．42 kN，结果表明:盾构施工对既有隧道的拱顶、底的轴力有较大的影响，地下街的底板、顶板的影响次之，而左右拱腰处的影响则较小。

表3 地下街、既有隧道的轴力变化情况Table 3 Axial forces of the commercial street and constructed tunnel with excavation steps of subway tunnel kN

5 结论

(1)盾构施工导致地下街顶板、底板发生不均匀沉降。顶板沿纵向最大沉降发生在对称面处，底板沿纵向发生扭曲变形，其最大沉降在盾构左线中心线处。

(2)盾构施工对既有隧道的影响存在一定范围。当盾构机开挖面距既有隧道2D范围内，既有隧道受到顶推力作用，拱顶、底竖向位移表现为隆起，在距既有隧道前方0．5D处隆起量最大;随着盾构机逐步穿越，既有隧道的拱顶、底由于地层损失均发生沉降，最大沉降发生在既有隧道的对称面处;在交叠区域以外，沉降值较小。

(3)盾构施工导致地下街及既有隧道产生附加弯矩和轴力，两者的变化趋势较为一致，均表现为先增大后减小，再增大再减小，直至趋于稳定。盾构开挖使地下街顶板及既有隧道的拱顶处于受拉的不利状态中，易导致结构出现开裂和发生渗漏，影响正常使用。

(4)既有建筑物的沉降值、附加内力值与顶推力相关。随着顶推力的增大，对土体的扰动加剧，沉降与附加内力均呈现出增大的趋势，其对既有隧道的影响要甚于地下街，但其影响有限。

［1］张凤祥．朱合华．傅德明．盾构隧道［M］．北京:人民交通出版社，2004．ZHANG Fengxiang，ZHU Hehua，FU Deming．Shield tunnel［M］．Beijing:China Communications Press，2004．

［2］Peek R B．Deep excavation and tunneling in soft ground，State of the Art Report［C］//Proc．7Int．Conf．on Soil Mechanics and Foundation Engineering，Mexico City，1969:225－290．

［3］ Liu Baochen．Ground surface movement due to underground excavation in China．Comprehensive Rock Engineering［M］．New York:Pergaman Press，1993:781 －817．

［4］Shinichiro Irnamura，Toshiyuki Hagiwara，Kenji Mito，et al．Settlement through above a model shield observed in a centrifuge［J］．Centrifuge98，Toyko，1998，713 －719．

［5］张志强，何 川．南京地铁区间盾构隧道“下穿”玄武湖公路隧道施工的关键技术研究［J］．岩土力学，2005，26(11):1711－1716．ZHANG Zhiqiang，HE Chuan．Research on key technique of shield tunnel construction beneath adjacent existing highway tunnel［ J］ ．Rock and Soil Mechanics，2005，26(11):1711 － 1716．

［6］陶连金，孙 斌，李晓霖．超近距离双孔并行盾构施工的相互影响分析［J］．岩石力学与工程学报，2009，28(9):1856－1862．TAO Lianjin，SUN Bin，LI Xiaolin．Interaction analysis of double holes extremely close approaching shield tunnels construction．［J］．Chinese Journal of Rock Mechanics and Engineering．2009，28(9):1856 －1862．

［7］姜忻良，贾勇，赵保建，等．地铁隧道施工对邻近建筑物影响的研究［J］．岩土力学，2008，29(11):3047 －3052．JIANG Xinliang，JIA Yong，ZHAO Baojian，et al．Analysis of influence of metro tunnel construction on adjacent buildings．［J］．Rock and Soil Mechanics，2008，29(11):3047－3052．

［8］骆建军，张顶立，王梦恕，等．地铁施工对管线的影响［J］．中国铁道科学，2006，27(6):124 －127．LUO Jianjun，ZHANG Ding li，WANG Mengshu，et al．Influence of metro construction on underground pipeline［J］．China Railway Science，2006，27(6):124 －127．

［9］王炳军，李宁，柳厚祥，等．地铁隧道盾构法施工对桩基变形与内力的影响［J］．铁道科学与工程学报，2006，3(3):36－41．WANG Bingjun，LI Ning，LIU Houxiang，et al．Effects of shield tunneling on adjacent existing loaded pile foundations［J］．Journal of Railway Science and Engineering，2006，3(3):36 －41．

［10］O＇Reilly M．P．New B．M．Settlements above tunnels in the UK － their magnitude and prediction［J］．Tunneling，1982，82:173 －181．