基于径向基函数响应面方法的超大跨悬索桥有限元模型修正
郁胜,周林仁,欧进萍,3
(1.大连理工大学建设工程学部,辽宁大连116024;2.华南理工大学土木与交通学院,广东广州510641;3.哈尔滨工业大学土木工程学院,黑龙江哈尔滨150090)
根据桥梁结构施工图纸建立合理的有限元模型来研究结构的静力和动力特性,是桥梁结构长期健康监测以及损伤识别、安全评定的基础[1]。在有限元模型中,由于模型参数误差以及有限元离散化等因素的影响势必导致建立的有限元模型的结构响应与真实结构响应之间存在一定的误差。模型修正技术是为了减小这种差异,获取结构真实状态模型的有效手段。目前,国内外学者提出了很多基于结构静力响应,动力响应和动静结合响应的模型修正方法[2-4],该方法主要包括矩阵型修正方法,参数型修正方法、子结构修正方法、灵敏度分析方法等[5-6]。然而对于超大跨悬索桥结构,由于结构构造复杂、杆件数量庞大、结构本身强烈的非线性等因素的影响,使模型修正更加复杂。对于这类复杂结构,前人提出的方法往往存在较低的优化效率和较低的优化精度等缺点。韩万水等[7]基于ANSYS软件的优化模块对四渡河深切峡谷特大钢桁架悬索桥进行了有限元模型修正。然而该方法需要根据待修正参数的变化多次调用有限元程序进行计算,降低了分析效率,同时软件自带的优化算法有限,难以与目前快速发展的智能优化算法结合起来,继而限制了优化的精度和效率。
起源于结构优化领域的响应面方法(RSM),近年来开始逐步在模型修正领域得到应用。任伟新等[8]用响应面方法对一座六跨连续梁桥进行模型修正,证实了该算法能够显著提高修正效率,易于工程实际应用;孔宪仁等[9]在利用改进的高斯径向基响应面方法对蜂窝板进行了修正,并取得了较好的修正效果;周林仁等[10]利用径向基响应面方法对斜拉桥实验室模型进行了修正,证实了该方法在斜拉桥的有限元模型修正中具有较高的精度和抗噪能力。任伟新等[11]针对响应面方法在结构模型修正方面的应用与研究进展进行了总结,并展望了该方法的发展方向。
响应面方法用显式的函数去拟合结构参数与结构输出之间复杂的隐式关系,易与优化算法结合,能以较小的计算量获取一定精度的计算结果。
本文用高斯径向基响应面对湖南某超大跨塔梁分离式悬索桥进行模型修正。首先利用灵敏度分析方法选取待修正参数和相应特征量;然后利用中心复合试验设计方法构造不同摄动水平下的待修正参数样本,通过有限元模型的静动力分析构造不同参数水平下的特征量样本;以待修正参数样本为输入量,特征量样本为输出量,基于径向基响应面模型逼近特征量和设计参数之间复杂的隐式函数关系,继而得到与结构对应的简化响应面模型。结合该超大跨悬索桥成桥试验监测数据,利用遗传算法对该桥的三维有限元模型进行修正。
1 模型修正过程和方法
1.1 径向基函数响应面模型
对于高度非线性问题,采用传统的响应面方法构造的全局响应面模型精度往往不高,所以,传统的方法只适合局部建模,而径向基函数(Radial Basis Function,RBF)可用于全局显式模型的建立。
径向基函数方法是一种插值方法。基于径向基函数(RBF)的响应面建模方法具有良好的适应性和精度等数学特性。根据文献[12]给出的Micchelli定理和文献[13]给出的最佳一致逼近理论中哈尔(Heaar)条件的等价定义,说明径向基函数是未知函数唯一的最佳一致逼近形式。文献[14]通过对不同形式的径向基函数的近似结果比较,发现对不同类型的测试函数,高斯径向基函数的均方根误差(RMSE)均较小,说明高斯径向基函数具有良好的拟合适应性、较高的精度和应用的广泛性。该函数目前被广泛应用于拟合低阶或者高阶的非线性模型。
最常用的径向基函数响应面模型形式为高斯径向基函数响应面模型,其表达式:
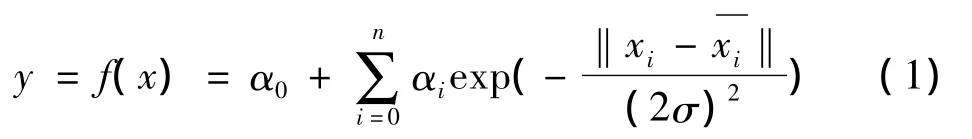
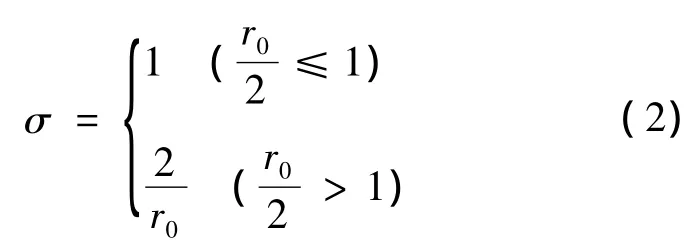
式中,r0为参数设计空间内最远两点的距离。
评价响应面模型有效性的标准主要有均方根误差(Root Mean Squared Error,RMSE)和复相关系数,其中RMSE→0和R2→1时,表示拟合的响应面模型具有较高的精度,其表达式为
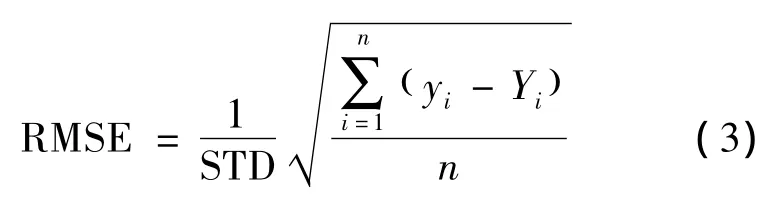
式中:n为样本数;Yi为响应面模型的预测值;STD为观测值的标准差。
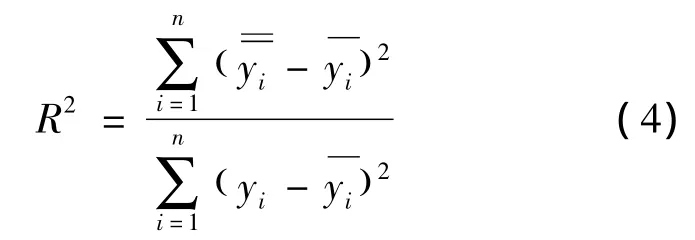
1.2 目标函数以及优化算法的选取
目标函数的构建以及优化算法的选取是模型修正中关键的步骤,而目标函数的构建直接决定优化方法的选取和优化问题的求解。为了使修正后的有限元模型能够在静力和动力特性上都能跟真实结构尽可能的接近,本文采用联合静动力特征信息构造残差型目标函数:
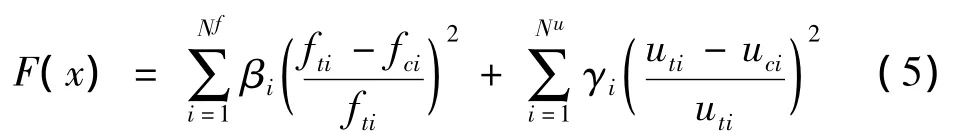
式中:βi和γi为权系数;分别表示测试频率和计算频率;Nf表示频率的数量;和分别表示测试静力位移和计算静力位移;Nu表示静力位移的数量。
基于径向基响应面方法的模型修正实际上就是解决多约束条件下的优化问题。遗传算法优化方法在解决多变量、非线性、多约束优化问题上都具有较好的全局搜索能力,因此本文采用遗传算法对优化问题进行求解。
2 工程概况
湖南某悬索桥为吉茶高速公路的控制性工程,桥位距吉首市区约20 km,于K14+576.30处跨越矮寨镇(G209 2303 km处)附近的山谷。该桥采用塔梁分离式设计,桥梁全长约1 073.65 m,悬索桥主跨1 176 m;主桥纵桥向设置0.80%的单向纵坡,主桥横桥向设2%横坡;桥面系宽度24.5 m,钢桁加劲梁全宽为27 m。全桥采用两根主缆索,矢跨比1/9.8,主索中心距为27 m,采用平面索布置;全桥采用71对吊索,吊索标准间距为14.5 m,端吊索的间距为29 m;主跨梁高(主桁中心线处)7.5 m。
2.1 静动力测试工况
图1所示为静力工况车辆加载位置示意图,本次荷载试验选用总重350 kN的加载车辆,其后两轴轴重与规范车辆荷载的后两轴轴重相同,如图2和图3所示。图4所示为大桥有限元模型理论分析时荷载布置图。图5所示为变形测点布置图,分别在钢桁梁主桁的 1/8(J08、C09)、1/4(J18、C19)、3/8(J27、C27)和跨中(Z35)设全站仪棱镜挠度测点(上下游共14测点)以监测钢桁架挠度。主塔、钢桁架以及主缆索测点均为上下游测点,钢桁梁纵漂测点采用上下缘测点。图6所示为模态测点位置。
2.2 初始有限元模型的建立
由于该大桥属于超大跨度的塔梁分离式悬索桥,结构大型而且复杂,为了建立该桥健康监测系统的基准模型,本文根据施工图纸,采用通用有限元软件ANSYS,基于APDL技术建立了该桥梁的三维有限元模型,如图7所示。该模型主要包括主缆、吊杆、钢桁梁、桥塔、钢纵梁和桥面板共6部分,未考虑锚碇和桩土相互作用。主缆和吊杆通过LINK10单元模拟,主梁、桥塔和钢纵梁等采用BEAM188单元;防撞护栏、抗风稳定板、检修通道和观光通道等通过质量单元MASS21施加;桥面预制板通过shell63单元模拟,桥面铺装等附属设施通过等效成预制板的材料密度施加;在梁端采用弹簧单元(combin14单元)模拟支座处的摩擦效应以及伸缩缝的影响。
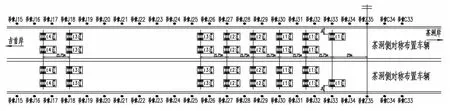
图1 静力工况车辆加载位置Fig.1 Truck positions under static loading cases
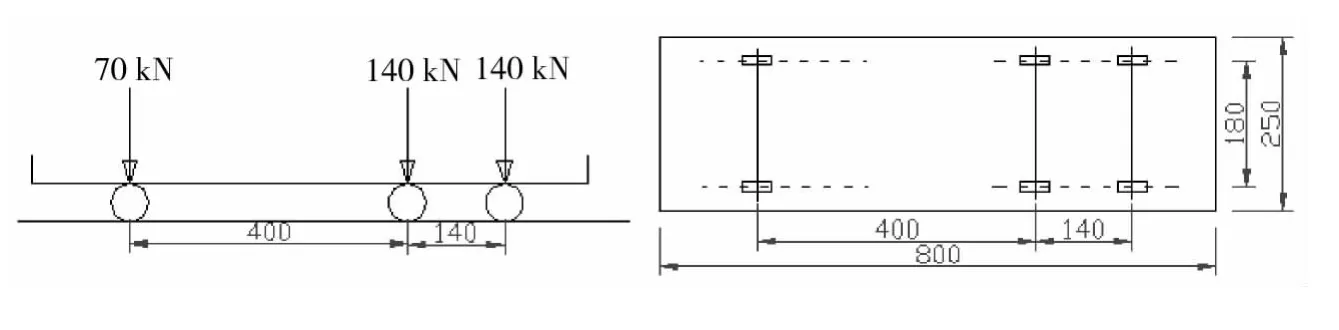
图2 加载车辆轴重、轴距及外形尺寸图/cmFig.2 Loading vehicle axle load 、wheel base、overall dimension/cm

图3 加载车辆Fig.3 Loading vehicle

图4 主加载工况理论分析模型加载布置图Fig.4 Load positions for finite element model under static cases

图5 主缆变形测点布置图Fig.5 Positions of measurement points for deformations

图6 大桥模态测试测点布置示意图Fig.6 Positions of measurement points for modes
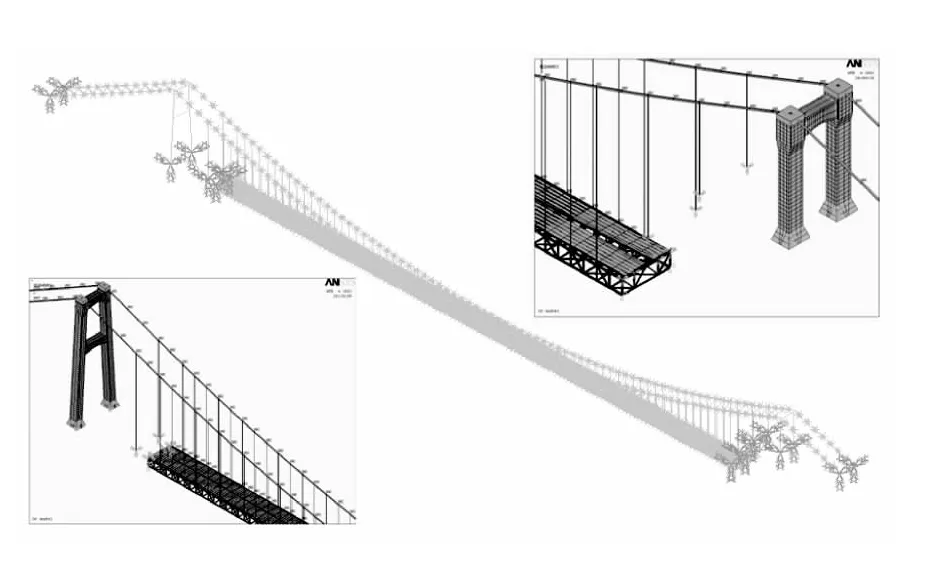
图7 初始有限元模型Fig.7 Initial finite element model
考虑到悬索桥的重力刚度对结构的特性具有显著的影响,同时为了保证计算结果的可靠性,在建立有限元模型时,主缆索的初始应变根据实验实测索力通过换算得到,并进行应力刚化。
2.3 初始有限元模型误差分析
本文根据成桥实验数据,对初步建立的有限元模型进行了相应的动静力分析,理论分析加载位置如图4所示,静力变形提取点如图5所示,计算结果如表1所示。动力分析选用实测横向两阶、竖向三阶频率与有限元计算结果进行对比分析,计算结果如表2所示,图8给出了振动模态。

表1 修正前模型计算位移与监测位移Table 1 Analytical displacements and monitoring displacements

图8 侧弯和竖弯振型对比Fig.8 Comparison of lateral bending、vertical bending vibrations modes

表2 修正前模型计算频率与监测频率Table 2 Analytical frequenciess and monitoring frequencies
从表1可以看出:初始有限元模型计算的静力挠度与实际监测的挠度相对误差均在5%以内,最大误差主要出现在吉首塔塔偏测点、钢桁梁挠度C19(5/8跨)测点、主缆索挠度测试C19测点,这几个监测点的误差均超过了10%,而剩余监测点相对误差均在10%以内。从表2可以看出,最大误差发生在一阶对称竖弯和二阶对称竖弯,误差达到了10%以上,其他频率误差均在10%以内。计算结果表明:初始有限元模型有效,但是静动力响应与实测响应之间仍然存在一定的偏差,因此需要对初始有限元模型做进一步的修正,以建立能够准确反映结构真实物理特性以及动静力特性的有限元模型。
3 有限元模型修正
3.1 修正参数以及特征量的选择
3.1.1 修正参数的选择
在有限元模型中,由于需要定义的物理参数众多,而超大跨悬索桥动力特性对每个物理参数的敏感程度不尽相同。因此,在超大跨悬索桥的有限元模型修正过程中,如果将所有的物理参数都给予考虑,不仅计算量大,不宜用于实际工程,而且往往会导致计算收敛困难;如果仅凭经验选取某些特定的参数,往往又会导致修正结果失真。为了提高修正效率,保证修正结构的可靠性,本文首先根据经验选取岩锚边吊索弹模、中央扣弹模、主缆索弹性模量、主缆索密度、吊索弹性模量、吉首塔主塔弹性模量、吉首塔密度、茶洞塔弹性模量、茶洞塔密度、加劲梁弹性模量、桥面系工字钢弹性模量、桥面板弹性模量、桥面板密度、主横桁上弦中间节点附加质量(抗风措施)、主横桁上弦边节点附加质量(上检修通道)和主横桁下弦1/8节点附加质量(观光通道)作为初始待修正参数。
本文采用目前工程中常用近似的算法(见(6)式)来计算特征值灵敏度[9]。

式中:δpi为第i个待修正参数的微小摄动量;δλj为第j阶特征值λj对应于待修正参数微小摄动后的改变量。
图9所示为频率灵敏度分析结果。根据此结果本文选取:主缆索弹性模量E1、主缆索密度D1、吉首塔主塔弹性模量E2、茶洞塔弹性模量E3、加劲梁弹性模量E4、桥面板弹性模量E5、桥面板等效密度D2和桥面系工字钢弹性模量E6作为待修正参数。由于桥面系工字钢与加劲梁是同一种材料,因此本文为了减少后期样本的计算量,将这2个参数合并成一个参数进行修正。

图9 频率对参数灵敏度Fig.9 Parameter sensibilities
3.1.2 特征量的选择
特征量作为修正问题的已知信息,信息量越多,理论上修正结果越准确,但是用于模型修正的信息必须要准确,如果误差过大,往往会导致修正结果失败或者修正结果验证失真。在目前的数据监测中,静力数据的测量由于受到噪声的影响较小,测量精度一般都较高,因此本文选取吉首塔顺桥向挠度、茶洞塔顺桥向挠度、钢桁梁J18(1/4跨)竖向挠度、钢桁梁J27(3/8跨)竖向挠度、钢桁梁Z35(1/2跨)竖向挠度、钢桁梁C27(3/4跨)竖向挠度、钢桁梁C19(5/8跨)竖向挠度,主缆索J18(1/4跨)挠度,主缆索Z35(1/2跨)挠度和主缆索C19挠度共计10个挠度作为静力特征信息;选取前五阶频率(一阶段对称侧弯、二阶反对称侧弯、一阶反对称竖弯、二阶对称竖弯和三阶对称竖弯)作为有限元模型的动力特征信息。
根据现有桥梁健康监测系统长期监测的数据表明,温度是影响桥梁结构振动特性的重要因素之一。Li等[16]采用峰值拾取法对润扬斜拉桥的实测加速度信号进行了模态参数识别,发现大桥的自振频率在1 d之中的变化量在1%~4%;Peeters等[17]对瑞士Z24-bridge进行了216 d的监测,发现在温度的影响下,前四阶频率的变化量分别14%,18%,16%和17%。因此,温度对桥梁结构的振动特性有非常显著的影响。但是,鉴于目前温度对结构振动特性的影响还不能准确地进行量化处理,因此本文在做模型修正时将不考虑温度效应对特征信息的影响。
3.2 响应面建模以及有效性检验
基于径向基函数的响应面模型修正,包括响应面模型的建立和模型的修正2个主要部分,步骤如下:
(1)生成样本。采用中心复合实验设计(CCD)方法生成了7个待修正参数3水平的输入样本。为了保证修正后的模型参数都在合理的范围内,三水平分别为基准值的0.8,1.0和1.2倍,即摄动幅值水平在±20%。根据实验设计工况,利用有限元模型分别计算每种工况对应的特征值作为输出样本。
(2)建立响应面模型。基于上一步计算的样本,根据式(1)建立表征待修正参数与特征量之间复杂关系的高斯径向基响应面模型,待定参数σ根据式(2)计算。
参数主缆索的弹性模量E1、钢桁梁的弹性模量E4对第一阶频率和跨中钢桁架挠度的响应面模型分别如图10(a)和图10(b)所示。由图可见,各响应面都比较连续光滑,有利于模型修正中的优化求解。

图10 高斯径向基响应面模型Fig.10 The GA response surface model of frequency、displacement with respect to the design parameters of E1 and E4
(3)响应面模型精度检验。采用相对均方根误差RMSE或复相关系数R2对已建立的响应面模型进行精度检验。当建立的响应面模型不能满足要求时,需要重新调整样本分布,重新回到第一步。特征量的高斯径向基响应面模型拟合精度如图11所示,复相关系数均R2≥0.6,RMSE的值均较小,说明建立的响应面模型具有较高的精度。

图11 基于复相关系数以及RMS的响应面模型有效性检验Fig.11 Validity evaluation of response surface based on the coefficient of determination(a)and the relative mean square error(b)
(4)模型修正。根据步骤(3)获得的满足精度要求的响应面模型,采用实测的特征量信息构造目标函数(如式(5)所示),继而采用遗传算法进行优化求解。
3.3 基于仿真数据的模型修正
为了检验已建立的高斯径向基响应面模型对于超大跨悬索桥有限元模型修正的有效性,本文先利用仿真数据来进行模型修正。基于上文中已经建立的高斯径向基响应面模型,结合遗传算法对该桥待修正参数进行修正。步骤:(1)在参数设计空间内,对7个待修正参数做随机摄动,继而得到各参数的摄动因子(摄动值/理论值);(2)对经过参数摄动后的有限元模型进行分析,计算响应的动力信息特征量和静力信息特征量;(3)基于上述信息特征量对有限元模型进行修正,检查各待修正参数的修正因子是否收敛于摄动因子,同时检查响应面模型的预测值与有限元计算值之间的误差。模型修正后待修正参数的修正因子和摄动因子结果如图12所示,修正误差如表3所示。

图12 摄动因子与修正因子Fig.12 Perturbation factor and correction factor

表3 基于仿真数据的修正结果Table 3 Results of model updating based on numerical simulation
通过表3可以看出,修正因子非常接近摄动因子,所有参数的修正误差均在5%以内,最大误差发生在桥面板弹性模量E5上,误差为3.02%。
3.4 基于监测数据的模型修正
在修正中,目标函数、样本和静动力特征信息与上文相同。考虑到边界条件对模型的静动力特性有重要影响,因此将钢桁架两端的弹簧刚度也作为修正参数进行修正,分别为S1和S2。基于实测数据的各待修正参数的修正因子如表4所示。

表4 基于实测数据的修正结果Table 4 Results of model updating based on tested data
修正前后动力静力特征信息的误差分别见表5和表6所示。从修正结果中可以看出,修正后的误差有所减小,误差分布更为均匀。表7表示修正前后主缆索锚跨部位主缆索力的变化,从表中可以看出,修正后主缆索力减小,主要原因是修正后桥面部位的等效质量较修正前明显减小。结合表5和表7可以看出,模型修正前后主缆索的索力相应减小,但结构振动前五阶频率中有的相应减小有的相应增大。

表5 模型修正前后自振频率误差Table 5 Error of frequencies before and after model updating

表6 模型修正前后形变误差Table 6 Error of displacements before and after model updating
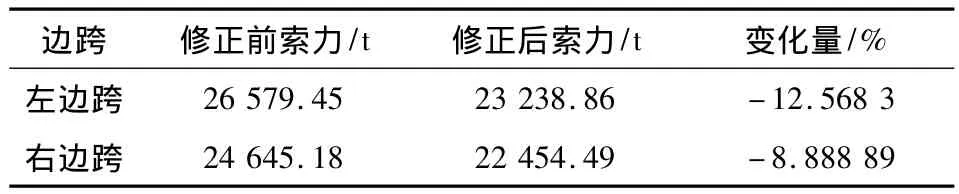
表7 模型修正前后主缆索锚跨部位索力变化Table 7 Changes in cable tension before and after model updating
基于仿真数据的修正结果表明:修正因子较好地收敛于摄动因子;而基于实测数据对模型进行修正后,其修正结果仍存在一定的误差,但特征信息的误差分布更加均匀。因此本文认为,导致这种情况的原因有如下2种:(1)实测数据存在一定的测试误差,并且特征量数据(如自振频率)没有考虑温度效应的影响,在模型修正中,各特征量的误差在修正结果中得到累积。(2)在构建响应面模型时,样本数据可能不包含某些实测特征信息值,从而导致部分实测特征信息处于响应面模型之外,在修正过程中,响应面的预测误差继而会放大。
4 结论
(1)基于仿真数据的修正,修正因子严格收敛于摄动因子,修正误差均在3%以内,说明了该方法的有效性;基于实测数据修正后的目标特征量的相对误差有了一定的减小,但误差依然较大,该误差可以认为主要是实测数据的测试误差以及忽略温度效应对结构自身振动的影响引起的。
(2)径向基响应面模型能够较好地拟合待修正参数与模型静动力特征信息之间复杂的隐式函数关系;通过湖南某超大跨悬索桥有限元仿真数据以及该桥成桥试验监测数据的模型修正,表明该方法适用于超大跨悬索桥梁的有限元模型修正。
(3)基于径向基函数响应面方法的模型修正可以避免传统模型修正过程中需要反复调用有限元程序的通病,并且易与智能优化算法结合起来搜索最优解,从而减少了计算成本,极大地提高了计算效率和精度,在工程中有实际应用价值。
[1]Ou J P,Li H.Structural health monitoring in mainland China:review and future trends[J].Structural Health monitoring - an International Journal,2010,9(3):219 -231.
[2]Jaish I B,REN Weixin.Structural finite element model updating using ambient vibration test results[J].Journal of Structural Engineering,2005,131(4):617 -628.
[3]Estes A C,Asce M,Frangopol D M,et al.Updating bridge reliability based on bridge management systems visual inspect ion result s[J].Journal of Bridge Engineering,2003,8(6):374 -382.
[4]宗周红,夏樟华.联合模态柔度和静力位移的桥梁有限元模型修正方法[J].中国公路学报,2008,21(6):43-49.ZONG Zhouhong,XIA Zhanghua.Finite element model updating method of bridge combined modal flexibility and static displacement[J].China Journal of Highway and Transport,2008,21(6):43 -49.
[5]ZHAO Jun,Dewolf J T.Sensitivity study for vibrational parameters used in damage detection [J].Journal of Structure Engineering(ASCE),1999,125(4):410 -416.
[6]HOU Jilin,Jankowskil,OU Jinping.A substructure isolation method for local structural health monitoring[J].Structural Control& Health Monitoring,2011,18(6):601-618.
[7]韩万水,王涛,李永庆,等.大跨钢桁架悬索桥有限元模型实用修正方法[J].交通运输工程学报,2011,11(5):18 - 27.HAN Wanshui,WANGTao,LI Yongqing,et al.Practical updating method of finite element model for long-span steel truss suspension bridge[J].Journal of Traffic and Transportation Engineering ,2011,11(5):18 - 27.
[8]任伟新,陈华斌.基于响应面的桥梁有限元模型修正[J].土木工程学报,2008,41(12):73 -78.REN Weixin,CHEN Huabin.Response-surface based on finite element model updating of bridge structures[J].China Civil Engineering Journal,2008,41(12):73 -78.
[9]孔宪仁,秦玉灵,罗文波.基于改进高斯径向基函数响应面方法的蜂窝板模型修正[J].复合材料学报,2011,28(5):220-227.KONG Xianren,QIN Yuling,LUO Wenbo.Improved gaussian RBF response surface method-based model updating for the honeycomb sandwich panel[J].Acta Materiae Compositae Sinica,2011,28(5):220 -227.
[10]周林仁,欧进萍.基于径向基函数响应面方法的大跨度斜拉桥有限元模型修正[J].中国铁道科学,2012,33(3):8-15.ZHOU Linren,OU Jinping.Finite element model updating of long-span cable-stayed bridge based on the response surface method of radial basis function[J].China Railway Science,2012,33(3):8 -15 .
[11]邓苗毅,任伟新.基于响应面方法的结构有限元模型修正研究进展[J].铁道科学与工程学报,2008,6(3):42-45.DENG Miaoyi,REN Weixin.Study on structure finite element model updating based on response surface methodology[J].Journal of Railway Science and Engineering,2008,6(3):42 -45.
[12]Micchelli C A.Montgomery.Interpolation of scattered data:distance matrices and condditionally positive definite functions[J].Constructive Approximation,1986(2):11-22.
[13]于志玲,张阳.最佳一致逼近理论中哈尔(Haar)t条件的等价定义[J].南开大学学报:自然科学版,2006,39(3):101-103.YU Zhiling,ZHANG Yang.The equivalent definition of haar condition in best uniform approximation theory[J].Acta Scientiarum Naturalium Universitatis Nankaiensis,2006,39(3):101 -103.
[14]隋允康,宇慧平.响应面方法的改进及其对工程优化的应用[M].北京:科学出版社,2011.SUI Yunkang,YU Huiping.The improvement on response surface methodology and their applications to engineering optimization[M].Beijing:Science Press,2011.
[15]Fang H B,Horstemeyer M F.Global response approximation with radial basis function[J].Engineering Optimization,2006,38(4):407 -424.
[16]Ding Y,Li A.Structural health monitoring of long-span suspension bridges using wavelet packet analysis[J].Earthquake Engineering and Engineering Vibration,2007,6(3):289 -294.
[17]Farrar C R,Cornwell P J,Doe bling S W.Structural health monitoring studies of the alamosa canyon and I-40 bridges los alamos national laboratory report LA-13635 - MS[R].2000.

