抑制CRTSⅡ型轨道板与水泥沥青砂浆离缝的技术措施研究

王雪松，曾志平，2，元 强，郭建光，张捍东

(1．中南大学土木工程学院，湖南 长沙410075;2．中南大学重载铁路工程结构教育部重点实验室，湖南长沙410075;3．沪昆铁路客运专线江西有限责任公司，江西南昌330002)

随着我国高速铁路的大量兴建，无砟轨道因其具有的平顺性，稳定性，耐久性和少维修等优点而得到了快速发展与广泛的应用。CRTSⅡ型板式无砟轨道是我国通过对德国博格板的引进、消化、吸收与再创新得到的一种高速铁路轨道结构，目前，已经在京津，京沪，沪杭等多条客运专线上使用［1］。它主要由钢轨，扣件，轨道板和水泥沥青砂浆和支承层(底座)等部件组成［2］。其中，水泥沥青砂浆(后文简称:砂浆)充填层是它的重要组成部分，同时也是无砟轨道结构体系中最薄弱的环节，其破坏形式主要体现为轨道板与砂浆充填层之间的离缝，并将导致进一步的对无砟轨道的破坏［3］。我国经过多年的研究实践发现，温度梯度荷载是产生轨道板与砂浆充填层离缝的主要原因之一。

为此，本文将轨道板与砂浆层之间的连接分为完全黏结和沿轨道板四周脱黏2种情况，并分别建立热－结构耦合分析有限元模型，进行理论计算和分析研究，并与其他几种方法和实测数据进行对比来验证模型的可靠性。从而为轨道板与砂浆层之间的离缝现象深入、系统的研究提供依据，为实际工程提供指导。

1 CRTSⅡ型板式无砟轨道理论计算模型

1．1 理论计算模型

根据CRTSⅡ型板式无砟轨道的结构特点，将钢轨以空间梁单元模拟;轨道板，砂浆和支承层(底座)以实体单元模拟;钢轨与轨道板及支承层(底座)与基础之间的竖向连接以线性弹簧单元模拟，再用弹簧单元模拟扣件和轨下基础的约束作用［4－6］;为了考虑扣件的尺寸效应，将每个钢轨节点与其对应扣件尺寸范围内的轨道板节点均相连;轨道板与轨道板之间设置纵向连接实体单元，通过改变该单元的弹性模量，模拟轨道板与轨道板是否纵连，通过改变扣件弹簧刚度可以模拟是否有钢轨和扣件约束，计算模型示意图如图1所示。另外，在轨道板下表面节点与水泥沥青砂浆上表面节点之间设置弹簧单元连接，当轨道板与砂浆层以完全黏结方式考虑时，该弹簧为刚度很大的线性弹簧单元;而当轨道板与砂浆层沿轨道板四周脱黏时，使轨道板四周的弹簧单元刚度为0，其他弹簧单元的刚度保持不变即可。

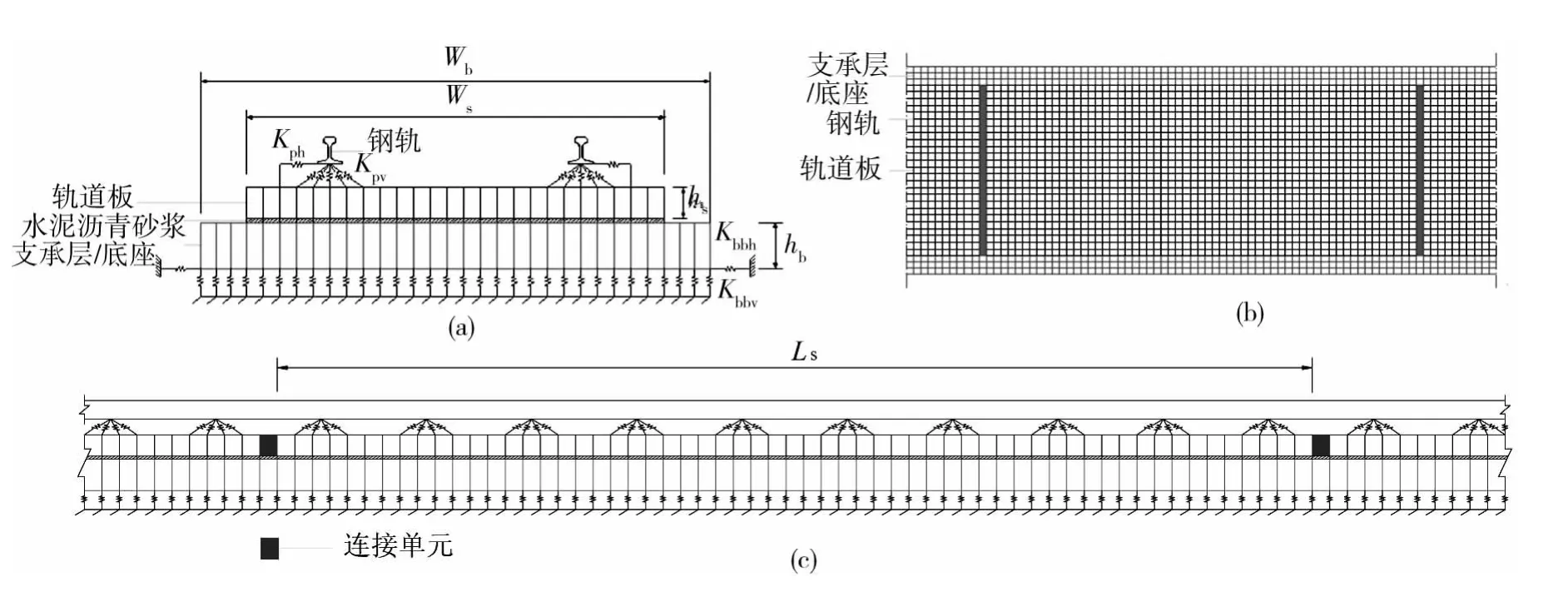
图1 板式无砟轨道理论计算模型Fig．1 Model of slab track

图1中各符号的具体意义为:Kpv和Kph为扣件垂向和横向刚度(N/m);Ls为轨道板长度(m);Ws为轨道板宽度(m);hs为轨道板厚度(m);Wb为支承层(底座)宽度(m);hb为支承层厚度(m);Kbbv和Kbbh为基础的垂向和横向刚度(N/m)。

1．2 程序的编制及模型验证

基于计算机语言MATLAB，对上述的有限元模型进行编制相应的计算程序，并采用3种方法对程序的可靠性进行验证，程序中所用到的主要计算参数如表1所示。

表1 CRTSⅡ型轨道板结构模型各参数Table 1 Calculation parameters for CRTSⅡslab track

(1)首先与解析法中最常用的戈希法进行对比。以CRTSⅡ型轨道板为例，不考虑重力，砂浆，钢轨和扣件约束的条件下，取轨道板上下表面温差为－10℃，本模型计算得到的轨道板的最大翘曲变形值为2．029 mm，而戈希法计算的结果1．999 mm。

(2)再取 CRTSⅡ型轨道板的温度梯度为－0．275℃/cm，轨道板之间不纵连，计算出轨道板的翘曲变形最大值为0．460 mm，而文献［3］中的ANSYS模型计算结果为0．473 mm。

(3)另外，2012年7月27和28日在某客运专线某特大桥的CRTSII型板式无砟轨道的施工现场，选择了4块轨道板进行24 h全天候监测，实测CRTS II型轨道板上下表面温差为－7℃时，轨道板最大竖向相对位移为0．76 mm，而本模型的计算结果为0．731 mm。

从上述3种对比的结果可以看出:本模型与解析法，ANSYS有限元法和实测的数据均有很好的一致性，可以用来进行CRTS II型板式无砟轨道轨道系统的受力与变形分析。

2 轨道板与砂浆完全黏结情况下轨道系统受力与变形分析

由于CRTS II型板式无砟轨道的轨道板表面积较大，常年暴露在大气环境之中，混凝土的热传导性能又很差，环境气温的变化必将导致轨道板沿厚度方向出现温度梯度［4］，在太阳光的照射下，轨道板的上表面温度高于下表面，这就产生了正的温度梯度;反之当因黑夜降临，冷空气侵袭和突然降雨等作用，轨道板的上表面温度骤然降低则产生了负的温度梯度。温度梯度会使轨道板产生竖向的翘曲变形和翘曲应力。

我国的高速铁路大部分都是铺设在桥梁上的，因此，本文以桥上CRTS II型板式无砟轨道为例，选取轨道板上下表面温差(由负温度梯度换算而来)为－5，－10和－15℃ 3种负温差，分别计算3种约束工况条件(轨道板之间不纵连;轨道板之间纵连、但无钢轨和扣件约束;轨道板之间纵连、并且有钢轨和扣件约束)下轨道板的翘曲变形与砂浆的拉伸量和拉应力。具体的计算结果见表2～4，变形图如图2和图3所示。

表2 工况1的轨道竖向变形与砂浆竖向应力Table 2 Slab vertical deformation and mortar vertical stress of the first working condition

表3 工况2的轨道竖向变形与砂浆竖向应力Table 3 Slab vertical deformation and mortar vertical stress of the second working condition

表4 工况3的轨道竖向变形与砂浆竖向应力Table 4 Slab vertical deformation and mortar vertical stress of the third working condition

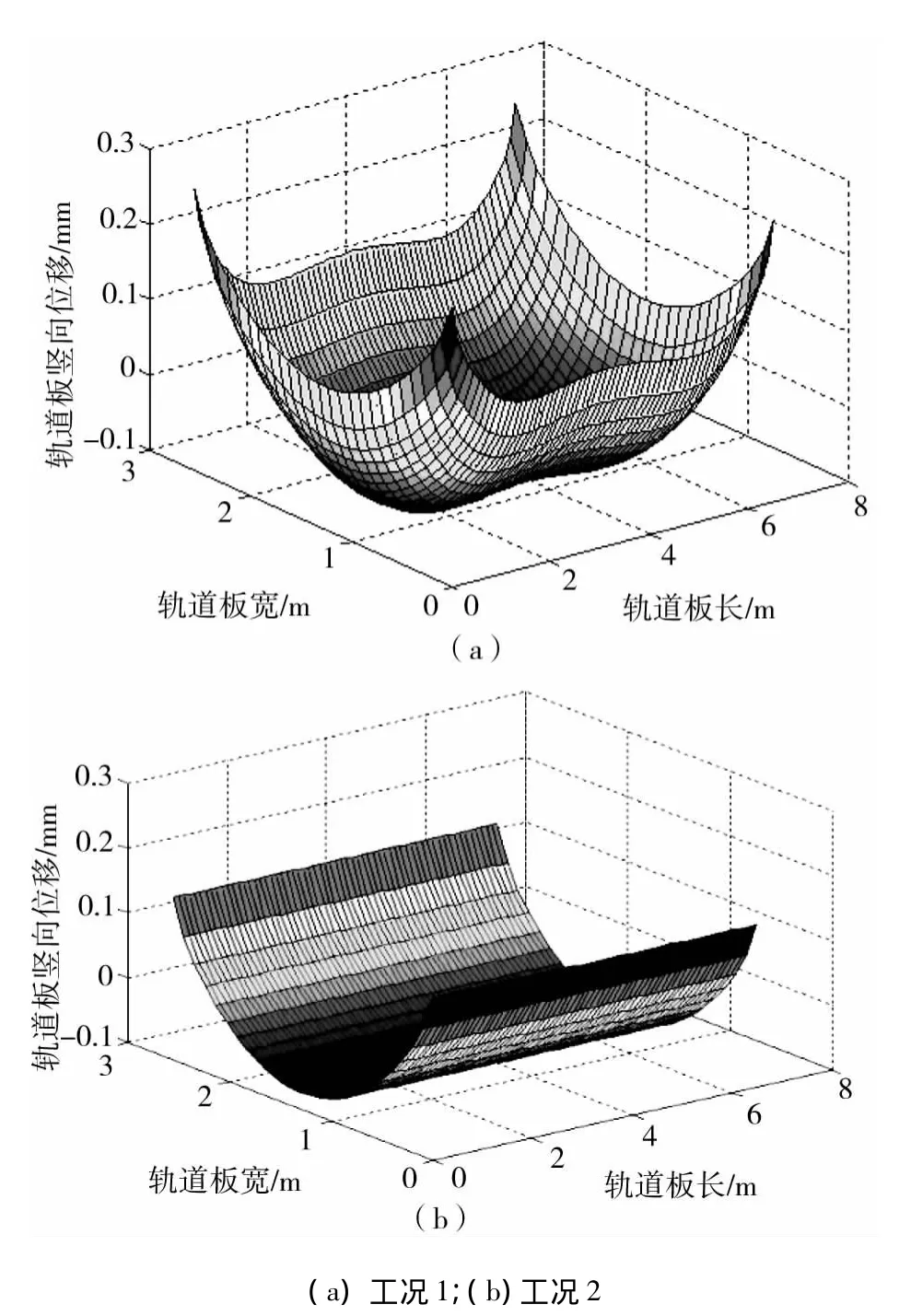
图2 工况1和工况2轨道板翘曲变形(－10℃)Fig．2 Slab warping deformation of the first and second working condition(－10℃)

由表2～表4可知:同种工况下轨道板的翘曲变形、砂浆的最大变形量和最大拉应力均随着温度梯度的增大而增长。对比表2和表3，我们可以看出:当轨道板纵连后，轨道板的变形、砂浆的最大拉伸量和最大拉应力都有显著的减小;再对比表3和表4，我们发现:当轨道板纵连后再对轨道板进行钢轨和扣件的约束，轨道板的变形、砂浆的最大拉伸量和最大拉应力并没有得到很大的抑制。同时，由图2(b)和图3所示的轨道板的翘曲变形图也可以发现钢轨和扣件对轨道板的变形几乎没有影响。另外，由表4可知钢轨的上翘与下沉位移都很小，这说明负温度梯度对钢轨平顺性影响很小，体现了无砟轨道平顺性好的优点。

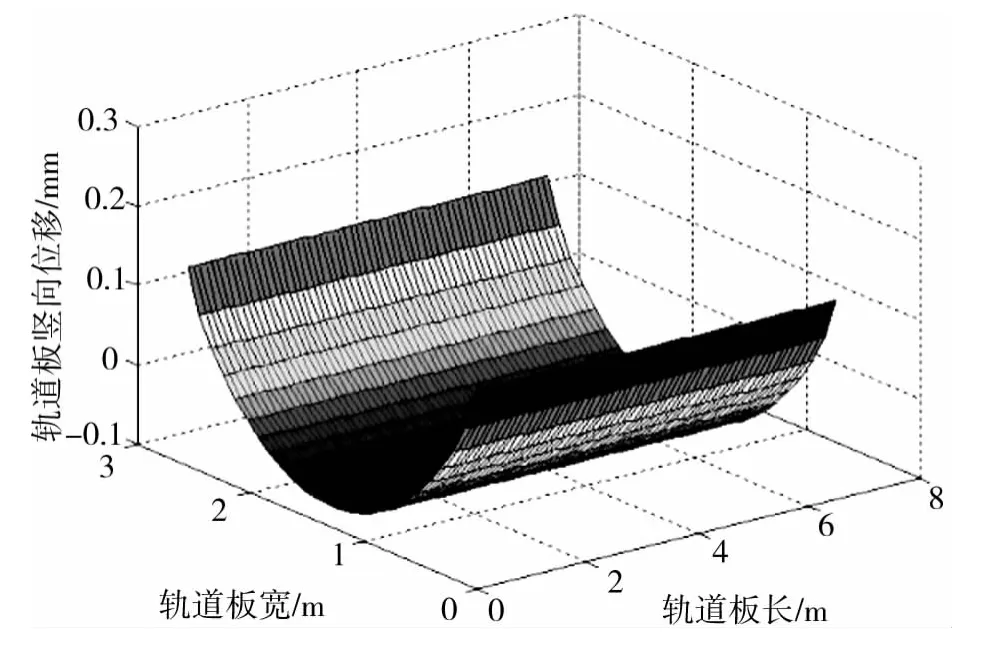
图3 工况3轨道板翘曲变形(－10℃)Fig．3 Slab warping deformation of the third working condition(－10℃)

3 轨道板与砂浆沿轨道板四周脱黏情况下轨道系统受力与变形分析

当轨道板与砂浆不再完全黏结而是沿轨道板四周出现了脱黏，即脱空现象，我们选取脱黏10 cm和20 cm 2种情况。仍然以桥上的CRTSⅡ型板式轨道为例，轨道板上下表面的温差还是－5℃，－10℃和－15℃ 3种，依然计算第2节中所述的3种约束工况条件下轨道板的翘曲变形，轨道板与底座之间的竖向相对位移和砂浆的应力。具体的计算结果如表5～表7所示(表中括号外为脱黏10 cm时的计算结果，括号内为脱黏20 cm时的计算结果)。

由表5～表7发现:同一工况下轨道板的翘曲变形和板边、板端、板角处的砂浆的最大拉应力仍然随着温度梯度的增大而增长;脱黏20 cm时轨道板的变形和砂浆最大拉应力(除板边外)均比脱黏10 cm时要大一些，但板边的数值很接近。再对比表5与表6可以发现:轨道板之间的纵向连接对轨道板变形和板边、板端、板角处的砂浆最大拉应力依然影响很大;表6和表7的对比结果说明:钢轨和扣件的约束对这些影响都很小。表7中钢轨的变形量依然很小，再次说明即使轨道板与砂浆层的脱黏后，负温度梯度对钢轨的平顺性影响仍然很小，进一步体现了无砟轨道高平顺性的优点。

表5 工况1的轨道竖向变形与砂浆竖向应力Table 5 Slab vertical deformation and mortar vertical stress of the first working condition

表6 工况2的轨道竖向变形与砂浆竖向应力Table 6 Slab vertical deformation and mortar vertical stress of the second working condition

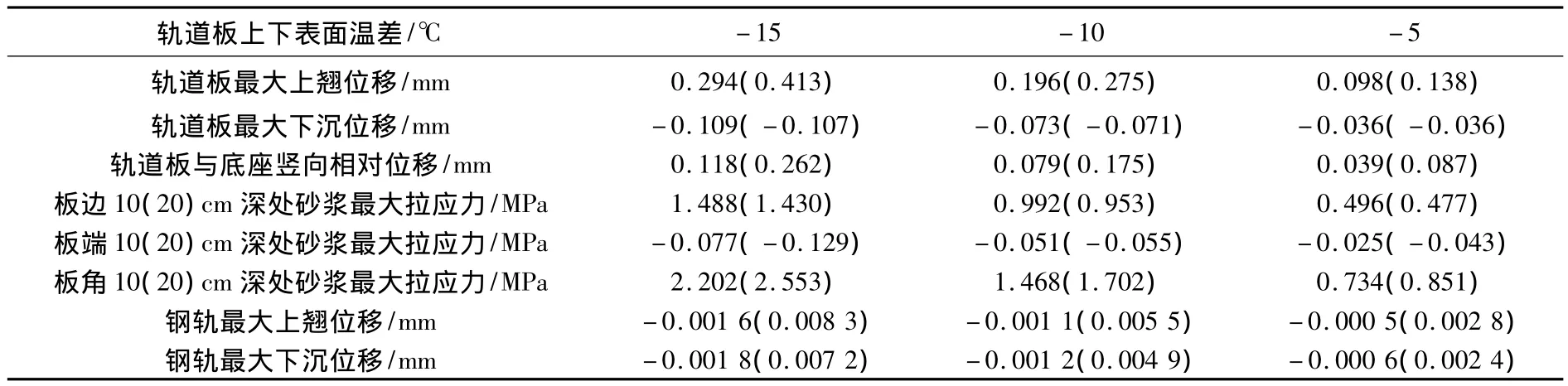
表7 工况3的轨道竖向变形与砂浆竖向应力Table 7 Slab vertical deformation and mortar vertical stress of the third working condition

4 砂浆离缝条件分析

由于轨道板与水泥沥青砂浆不可能是黏结得牢不可分，它们之间只是存在一定的黏结应力而连接在一起的。轨道板内部的温度梯度荷载使轨道板产生的翘曲变形将由轨道板的自重和轨道板与砂浆层之间的这种黏结应力来抵抗，当温度梯度超过一定的数值时轨道板与砂浆之间就会出现裂缝，所以，研究这个产生离缝的临界温度梯度就具有非常重要的意义。

根据前述的对轨道板变形和砂浆应力的计算研究，我们发现了温度梯度与砂浆的拉应力成线性关系，故可以通过前面计算得到了不同工况不同黏结条件下砂浆拉应力反推出某一黏结强度下的临界温度梯度。通过试验室一系列试验和实践经验，我们取轨道板与砂浆层之间的黏结强度为0．5，0.6，0．7 和0．8 MPa 4 种情况，在不同工况不同黏结条件下，板边、板端(工况2和3由于轨道板已经纵连，故板端不产生离缝)及板角处砂浆离缝时所对应的临界轨道板上下表面温差(℃)如表8所示。表8中①为轨道板与砂浆完全黏结;②为轨道板与砂浆沿轨道板四周脱黏10 cm;③为轨道板与砂浆沿轨道板四周脱黏20 cm。

由表8可知:在工况1条件下，轨道板板角的临界温度梯度最小，板边的临界温度最大;在工况2和工况3条件下，当完全黏结时板角与板边的临界温度梯度相等，当沿轨道板四周脱黏时，板角的临界温度比板边的小很多。在同一种工况条件下，与轨道板和砂浆层完全黏结相比，轨道板与砂浆层沿轨道板四周脱黏10 cm或20 cm时，板端和板边砂浆所允许的温度梯度均大大提高，但板角处砂浆所允许的温度梯度则提高的很少;而与轨道板与砂浆层沿轨道板四周脱黏10 cm相比，若轨道板与砂浆层沿轨道板四周脱黏20 cm，板端和板边砂浆所允许的温度梯度有所提高，但板角处砂浆所允许的温度梯度却反而降低了。

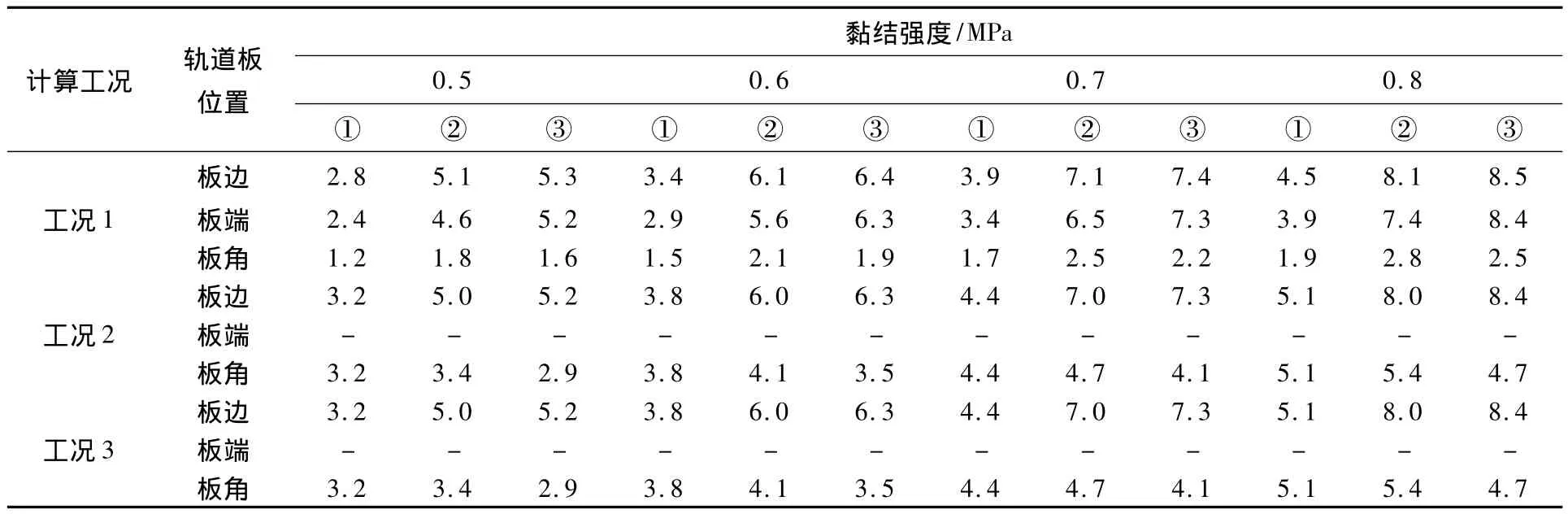
表8 不同黏结条件不同工况砂浆离缝所对应的临界温度梯度Table 8 Critical temperature of different bond condition in different working condition

5 结论

(1)对于不同约束工况和不同黏结条件，在温度梯度荷载作用下，轨道板翘曲变形，砂浆的最大拉伸量和最大拉应力均随着温度梯度增加而增大。

(2)不同的黏结条件下，轨道板之间的纵连均可以显著减小轨道板翘曲位移(减小约40%)和板角砂浆拉应力(减小约60%)，对板边砂浆最大拉应力影响不明显;同时钢轨和扣件的约束对轨道板翘曲位移与砂浆最大拉应力的影响很小，抑制砂浆离缝的作用很微弱。

(3)当轨道板之间不纵连时板角处最容易离缝，其次是板端，最后是板边;轨道板之间纵连后，板端基本上不会出现裂缝，而板角依然比板端更容易出现裂缝，但较轨道板不纵连时已有很大的提高。

(4)不同的约束工况条件下，轨道板与砂浆层沿轨道板四周脱黏情况下各处的临界温度梯度均比完全黏结时有所提高。

(5)不同的工况与不同的黏结条件下，增加轨道板与砂浆层之间的黏结强度，均有利于提高轨道板所允许的温度梯度而使轨道板不容易产生离缝。

(6)当轨道板板角处的砂浆一旦出现离缝，则其离缝的深度很容易继续扩大。

建议:(1)严禁在昼夜温差较大的季节或时间进行砂浆灌注施工;(2)砂浆灌注完毕，轨道板纵连之前，注意将轨道板进行覆盖，尽量减小轨道板的温度梯度的产生;(3)优化水泥沥青砂浆的性能，提高施工质量，从而获得其与轨道板之间较高的黏结强度。

［1］何华武．无砟轨道技术［M］．北京:中国铁道出版社，2005．HE Huawu．Ballastless track technology［M］．Beijing:China Railway Press，2005．

［2］高亮．轨道工程［M］．北京:中国铁道出版社，2010．GAO Liang．Track engineering［M］．Beijing:China Railway Press，2010．

［3］韩志刚，孙立．CRTSII型板式轨道轨道板温度测量与变形分析［J］．铁道标准设计，2011(10):41－44．HAN Zhigang，SUN Li．Temperature measurement and deformation analysis for CRTSⅡballastless track slabs［J］．Railway Standard Design，2011(10):41 －44．

［4］刘学毅，赵坪锐，杨荣山，等．客运专线无砟轨道设计理论与方法［M］．成都:西南交通大学出版社，2010．LIU Xueyi，ZHAO Pingrui，YANG Rongshan，et al．Design theory and method of ballastless track of passenger dedicated railway line［M］．Chengdu:Southwest Jiaotong University Press，2010．

［5］夸克工作室．有限元分析［M］．北京:清华大学出版社，2002．Quark Studio．Finite element analysis［M］．Beijing:Tsinghua University Press，2002．

［6］朱伯芳．有限单元法原理及应用［M］．北京:中国水利水电出版社，2004．ZHU Bofang．Application of the finite element method［M］．Beijing:China Water Power Press，2004．

［7］王继军，尤瑞林，王梦，等．单元板式无砟轨道结构轨道板温度翘曲变形研究［J］．中国铁道科学，2010，31(3):10－14．WANG Jijun，YOU Ruilin，WANG Meng，et al．Research on the slab temperature warping of the unit slab track system［J］．Chinese Railway Technology，2010，31(3):10－14．

［8］唐进锋，尹华拓，曾志平，等．温度梯度作用下板式无砟道岔岔区板力学特性分析［J］．铁道科学与工程学报，2011，8(1):24－28．TANG Jinfeng，YIN Huatuo，ZENG Zhiping，et al．Mechanical characteristic of slab track on switch area under temperature gradient［J］．Journal of Railway Science and Engineering，2011，8(1):24 －28．