基于马尔可夫转换模型的违约风险溢价预测研究

赵 峰，张 杰

（山东科技大学 经济管理学院，山东 青岛266590）

一、引 言

2007年7月美国爆发的次贷危机，其危害性正通过信用衍生品迅速向欧洲、日本、澳洲乃至全球蔓延，对全球金融市场造成了严重的影响。在全球金融市场剧烈动荡之际，国际热钱跨国流动频繁，信用衍生品一时间成为国际炒家狙击一国经济和牟取暴利的主要工具，致使全球金融交易市场风波迭起，信用衍生品对世界经济的冲击日益明显。从目前情况看，2013年世界经济有望延续复苏态势，但国际金融危机的深层次影响还在不断显露，凸显了长期性、艰巨性和复杂性，世界经济增速可能长期低位徘徊和面临下行的严重风险。当前的金融危机对金融业有明显的影响，并产生了较高的违约风险，虽然有些学者讨论次贷危机如何影响经济，但到目前为止，学术界、监管机构及各国央行对资本市场与汇率变动如何造成危机期间的违约风险溢价问题一直缺乏必要的研究。因此，深入研究金融违约风险溢价问题，对于信用风险的预防和有效管理等都具有重要的意义。

二、文献综述

违约风险溢价是财务管理模型中的一个重要内容，早期研究一般采用动态、连续的默认边界和随机利率模型，该结构模型的主要缺陷是公司价值的不确定性［1－2］。更早期的简化模型将单一跳跃过程中的违约强度归结为依赖于一些外生状态变量［3－4］。此外，已有大量研究成功解释了企业债券价格或单一名称 CDS（Credit Default Swap，CDS）利差违约风险溢价的驱动原理，如Longstaff等人指出债券息差是由于流动性不足造成的［5］；Elton等人提出不同企业和政府对违约风险债券息差的影响较大［6］；Blanco等人认为CDS息差作为公司敏感的特定要素而不能成为债券的利差［7］；Dupuis等人根据单一CDS息差流动性较低指数的信贷息差，推断出公司债券价格与税收及其流动性不足方面的关联关系［8］。总之，现有研究虽已构建了众多的期限结构模型来预测违约风险溢价，但效果仍不理想。

同时，有些学者用大量实证来寻找违约风险和宏观经济变量之间的关系，如Friedman等人指出企业破产和拖欠等的上升都在一个经济衰退的周期内，经济衰退的信息应该对应违约风险溢价的增加而起推动作用［9］；Stokes等人认为通货膨胀影响违约风险溢价，因为通货膨胀影响投入和产出价格，从而影响公司的业绩和盈利能力及未来违约的概率［10］113－117；Ewing认为货币政策冲击并导致违约风险溢价的即时波动，但随后风险溢价将趋于稳定［11］。

此外，对于通货膨胀所引发的违约风险溢价问题，国外学者也进行了大量研究。如Estrella指出收益曲线是未来实体经济活动的一个重要指标，向上倾斜的收益率曲线预示将来更高的经济活动和违约概率的减少［12］；Tang认为宏观经济影响企业现金流的过程，并有助于显著降低违约概率和信贷息差［13］；Duffie等人运用宏观经济变量，如工业生产增长来预测企业违约风险溢价问题［14］；Gharghori等人研究了违约风险和股票回报率之间的关系，得出了违约概率是负相关的观点［15］。简言之，现有的研究成果还需要进一步深入，即没有将违约风险溢价与随时间变化的动态因素联系起来。基于此，笔者利用马尔可夫转换模型来估算金融危机期间违约风险溢价问题，剖析在经济周期不同阶段的交替过程中违约风险溢价的变化。

三、马尔可夫违约风险溢价转换模型的构建

金融危机期间的违约风险溢价、股票的市场状况与宏观经济变量之间的关系可以由经济模型中的变量来解释，CDS指数息差成为首选的变量，其本质上代理违约风险溢价而不是债券的息差。若所构建经济模型具有潜在的生成周期，并能结合股市与宏观经济变动的概率，可用于预测违约风险溢价变化的信号；同时，该模型应允许违约风险溢价在不同经济周期下的方差切换，而且经济周期在任何给定的日期可推定为马尔可夫链，则可得如下马尔可夫转换的异方差和不同时间的参数模型：

现假设有两个阶段（经济稳定增长和经济危机）代表一个不可观测的过程表示为S，根据现行宏观经济状态让St的值为0或1，即St∈｛0，1｝为观察到的两种状态的马尔科夫转换变量，其演变的转移概率如下：

汉密尔顿假设S为一个一阶马尔可夫过程，这意味着现有经济发展阶段St仅仅依赖于前一时期St－1的发展阶段，完成该过程通过定义转换从一个阶段到另一个阶段的转移概率，此时违约风险溢价的变化或波动的概率状态为0或1，状态为0的马尔可夫模型意味着低波动的情况，即经济平稳发展［16］；状态为1则意味着极高波幅，即经济危机或经济很不景气。由于P01＝1－P00和P01＝1－P00的转换概率被完全定义为P00和P11，根据公式（1）～（6），如果定义经济周期内的稳定发展阶段为St＝0、经济危机阶段为St＝1，则可得结论：当βst＝时，经济处在平稳发展阶段；当βst＝时，经济处在危机或剧烈动荡阶段。

结合丁东洋等人的研究成果，在经济周期阶段转换之间，违约风险溢价和股票市场条件的关系可构建为如式（7）所示模型［17－18］。需要补充说明的是，对于公司违约风险以及违约风险与股票市场之间的关系则由经济主体的预期来决定，这将影响到债务及股票价值的价格，现有的研究也证实了单一制度模式下的信用违约掉期和股票市场之间的这种关系：

其中ΔCDSIt为从t－1到t（基点）CDS指数息差的变化，即CDS指数息差的日变动为从t到t－1之间（ΔCDSIt＝CDSIt－CDSIt－1）的一阶差分息差；ΔIRt为股市指数收益变动率；ΔIRVt为股指收益波动率；βit，St为时变系数，即当i＝0，1，2时的马尔可夫转换过程；vit为i＝0，1，2的误差项，且St∈ ｛0，1｝为观察到的两种状态的马尔可夫转换变量。因此，宏观经济变量之间的关系模型可扩展为：

其中ΔCPIt为居民消费价格变动指数，ΔIPIt为工业生产变动指数。

四、马尔可夫违约风险溢价预测转换模型的实证仿真

（一）数据描述

本文采用香港恒生指数（Hang Seng Index，HSI）CDS息差代理违约风险溢价作为实证对象。HSI CDS系列是在亚洲市场上流动性最强的单一名称信用违约掉期，而选择最有代表性的5年期恒生CDS是基于其高流动性的缘故。所收集的数据包括恒生CDS指数的每日收盘报价（引用买入价和卖出报价之间的中点），涵盖恒生指数有限公司从2006年3月至2009年11月期间所有的数据。香港恒生银行编制并公布的反映香港股票市场股价变动的股票价格指数，其构成并非以全部上市股份来计算。

恒生指数的计算方法是将选定的33种成分股票按其当天的收盘价，分别乘以上市股票数，加权合计出当天成分股的总市值，再用同样的方法算出基期日成分股的总市值，二者相比再乘以100，即得出当天的恒生指数。每日股价指数收益率计算如下：ln（SIt／SIt－1），运用 GARCH（1，1）模型来观察和计算每日股票收益指数波动情况［18］。GARCH（1，1）模型的定义如下：

其中α为滞后收益平方所分配的权重，β为滞后方差所分配的权重，ω为常量。因其简要且易于估计，并具有在随时间变化的各种波动情况下的成功建模经验，GARCH模型通常为预测的首选模型。对于宏观经济变量，通常使用月度数据来研究重要的经济指标，如居民消费价格变动指数（CPI）、工业生产变动指数（IPI）等，第一个变量通常用来观测通货膨胀的指标，第二个变量作为经济增长的预测指标，实证数据来源于恒生指数有限公司，表1总结了原始数据的统计信息。

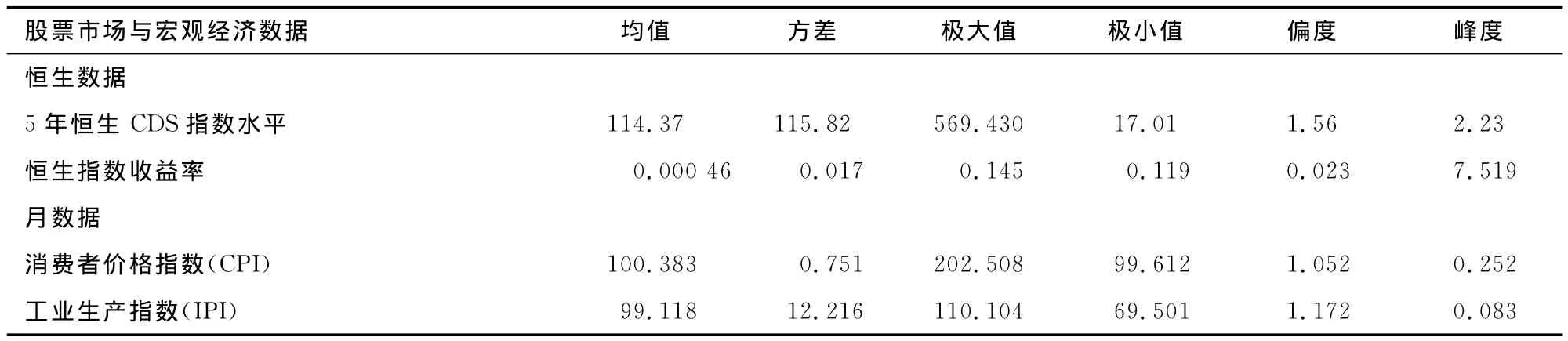
表1 初步统计表

5年期恒生CDS指数的标准差是很重要的数据，该CDS系列呈现出了正偏态特征，这表明所得到的回报为非正态分布。表1显示了恒生指数的一个正的超额峰度，突出了一个尖峰厚尾的特征（即相对尖顶的高斯概率分布）。

（二）参数估计

考察两个时期的数据：次贷危机前一个时期与次贷危机时期。作为实证调查，本文绘制了4年期每天香港恒生CDS指数水平和恒生33指数水平，见图1。这两个系列都经过标准化处理，其时间涵盖2007年1月21日至2010年8月30日。

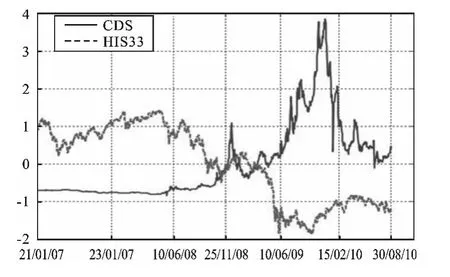
图1 HSI CDS水平和股指水平图

对于香港股市指数，从图1中可以发现恒生33指数从2008年6月大幅下跌，CDS指数息差扩大和暴跌共有三个阶段：第一个阶段在2008年6月10日之后，法国巴黎银行的附属公司暂停清算了两家对冲基金资产，这个日期标志着在CDS市场危机的开始；第二阶段从2009年开始，香港HSI CDS指数的价差在2008年12月中旬达到250个基点（然而在2006年3月的利差为28个基点）；第三阶段在2009年6月10日股市的CDS市场反应是异常迅速的。此外，笔者还注意到CDS利差水平与股价估值为负相关关系，当股票价格有明显增加趋势时CDS利差减少，反之亦然。通常情况下CDS溢价上升，公司的财务会遇到困难，因此应该限制其股价的跌幅。

金融危机的一般特点是经济波动性上升，因此应注意到HSI CDS指数波动的变化。为了更准确地测量危机期间的变化，可以运用指数加权移动平均波幅EWMA来定义和加权二次收益率与随着时间的推移指数递减的比重，EWMA模型被广泛用于危机期间的识别和预测。该模型被定义为：

其中λ为分配滞后差异的权重，且ω＝0、α＝1－λ、β＝λ。EWMA为GARCH模型的一个特殊情况，这两种模型之间的主要区别是GARCH模型采用均值回归，而EWMA模型不是，此特征能识别到波动性的突然增加，HSI CDS指数波动轨迹见图2。从图2中可以观察到HIS CDS指数波动在2008年6月突然增加，据此可以认为危机发生期间对应于这一时期的波动非常明显。表2是在危机开始期间计算每月CDS市场的EWMA波动情况，具体时间为2007年1月至2010年8月。

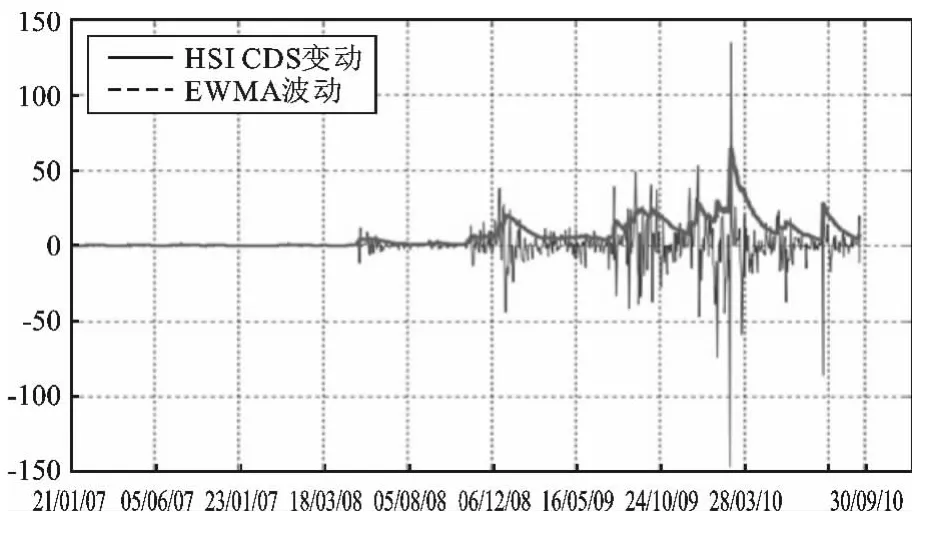
图2 HSI CDS指数的变化与EWMA波动曲线图

表2 EWMA每月波动变化表 单位：%

从表2可以看出，2008年5月开始的危机期间CDS利差指数的波动性已经明显增加，从2008年4月的28．73%增加到2008年5月的84．15%，从而可以识别两个子阶段：危机发生前的阶段，此时HSI CDS利差波动率特别低，这个阶段为从2007年1月至2008年4月；经济危机发生阶段，时间跨度为2008年5月至2010年9月。在第一阶段CDS溢价不仅低而且稳定，平均为23个基点，在此期间违约率很低，投资者的风险偏好较高；在危机阶段CDS保费呈现急剧增加的状态，2010年1月达到569．28个基点。

（三）马尔可夫转换过程

根据式（7）与式（8）对香港市场CDS利差指数进行测算，结果见表3。表3中模型1的数据采用了每日数据，模型2的数据采用了月度数据。若在相同的市场状态下，处在t时刻经济稳定状态下的概率（p＝P00）与t－1时刻的概率相同，为0．668 512；在t时刻经济处在危机状态下的概率（q＝P11）与处于高度波动状态t－1时刻的概率为0．652 384。这些高概率情况说明市场要么大幅波动、要么平稳发展，整个经济运行始终要保持这种规则，这也符合马尔可夫转换过程。同时，表3显示该指数回报率的方差波动在1%的水平（0．012 016），但在统计学上该显著性指数收益率的方差并不明显（0．011 325）。调查结果表明，在金融危机期间的违约风险溢价及股票市场条件之间的关系与经济波动的幅度有关，与经济所处的状态并不紧密。在金融危机期间，HSI CDS指数息差的股票指数收益率的波动变得高度敏感，时变参数的估计值如股指回报系数ΔIRt（β1t，0和β1t，1）、股指回报系数波动值 ΔIRVt（β2t，0和β2t，1）的变动过程如图3～5所示。在各图中，纵轴代表参数值，横轴代表观测值。由于这些参数遵循了马尔可夫转换过程，因此图中的每个参数有两种情况：状态1（经济危机期）和状态2（非经济危机期）。

表3和图3～5显示，违约风险溢价的变化、股市水平同宏观经济变量之间的关系与经济周期是相关的。图4表明在经济周期阶段交替变动的情况下，股票收益率对CDS利差变化的影响并不明显，股指收益率变动对CDS利差变动在危机前与危机期间也无影响。根据表3和图5中的实证结果，股指收益率的波动正好印证了经济周期阶段转换期间CDS利差的变动趋势。

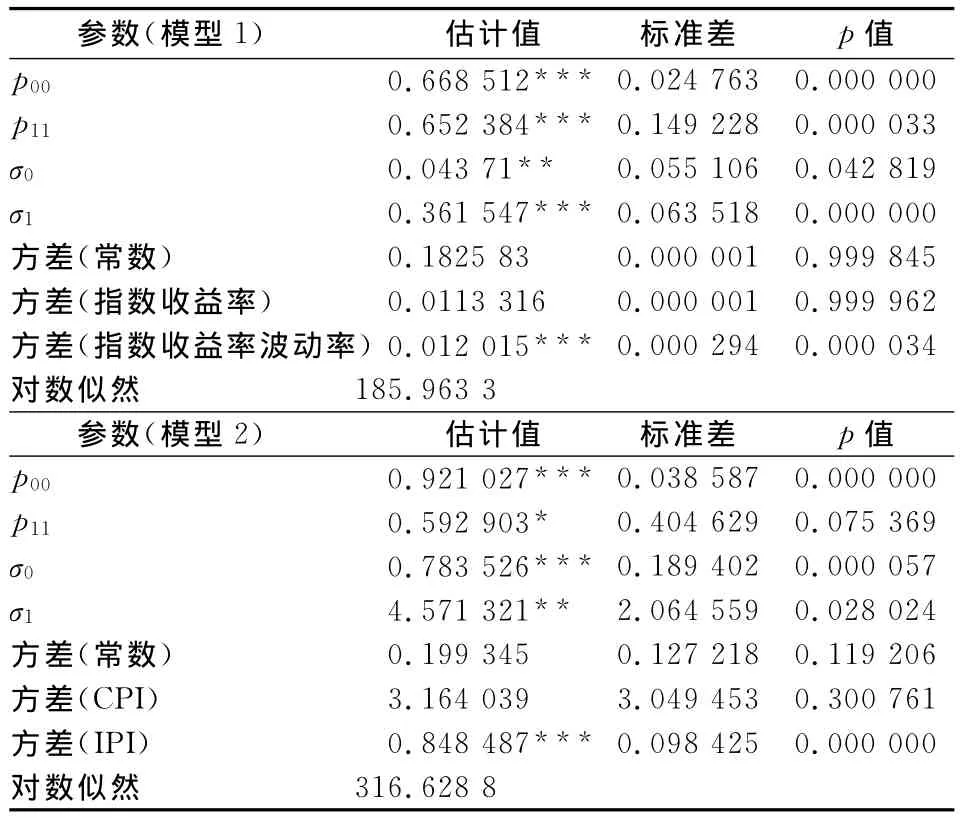
表3 香港市场估计结果表

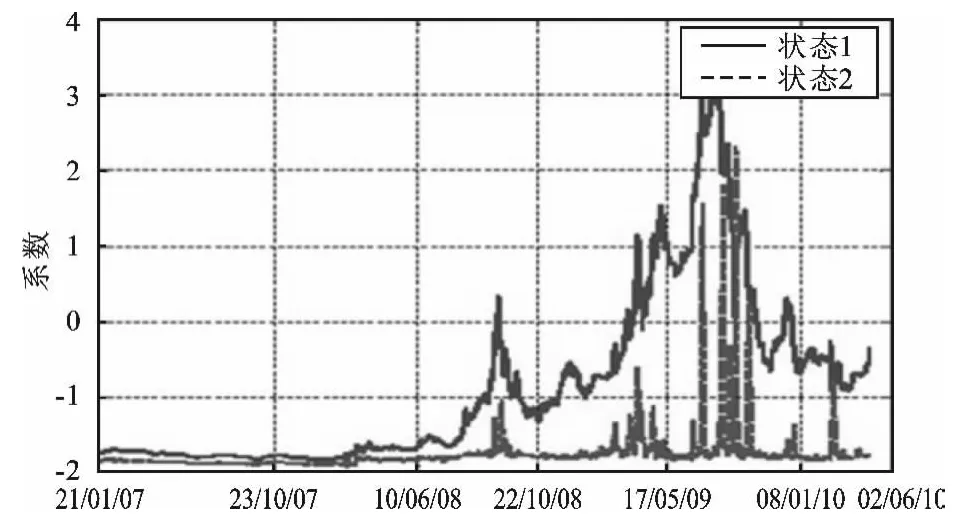
图3 经济阶段交替下时变常量估计值图

图4 马尔可夫转换过程中时变系数ΔIRt估计值图

图5 马尔可夫转换过程中时变系数ΔIRVt估计值图

模型2的估算结果表明，经济状态为0与经济状态为1的波动性不同，在统计学上更具有显著性特征。同时，模型1、2的估算结果还表明金融危机与整个经济运行态势相关，违约风险溢价和宏观经济变量之间紧密相关。然而，此时的工业生产指数在统计上具有显著性，达到了1%的水平（0．848 561），而居民消费价格指数并不显著，时变参数估计值的变化如图6～8所示。

图6 马尔可夫转换过程中时变参量估计值图

图7 马尔可夫转换过程中时变系数ΔCPIt估计值图

图8 马尔可夫转换过程中时变系数ΔIPIt估计值图

（四）实证结果的讨论与分析

当模型参数估计值测定后，CDS每日收盘价的息差与当时利差方差估计概率表现出了较高的相关性，考虑到整个样本的观测计算，这些概率即为所谓的平滑概率，作为一个马尔可夫转换的例证，图9表明平滑概率具有高度波动性规律，即在给定的t－1时间内，市场也呈现高度波动性规律。

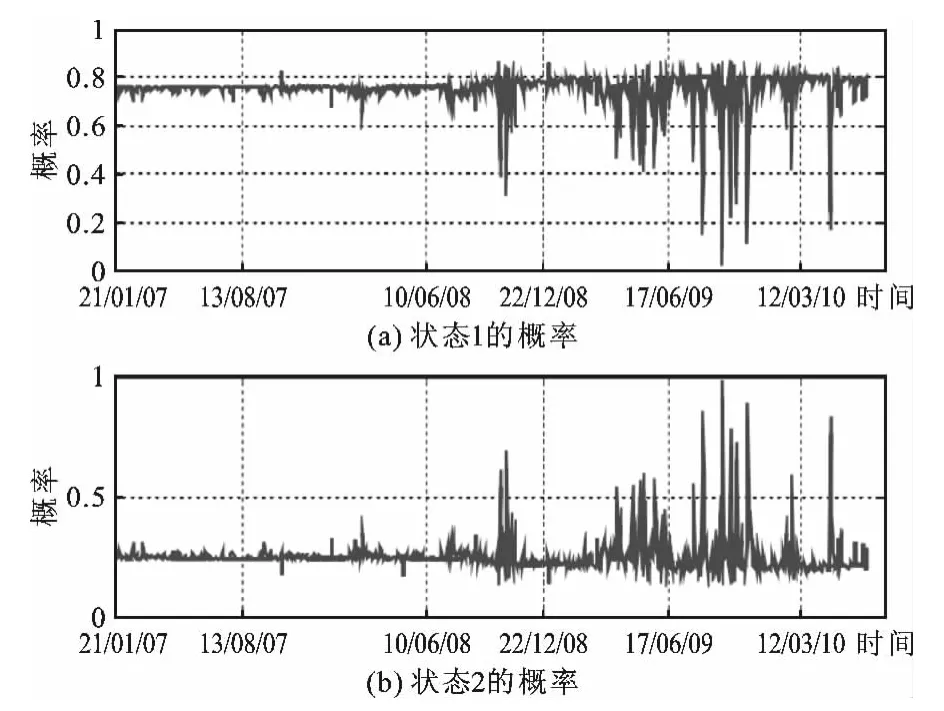
图9 马尔可夫转换过程中的平滑概率图

图9中所示的平滑概率揭示了经济周期转换阶段的时机，也表明经济发展呈现了高度波动性规律。图9中（a）图的实线代表跳跃情况，与次贷危机对香港CDS市场影响相匹配。在2008年7月以后，图9中（b）图显示的平滑概率以不规则的时间间隔大幅冲高，这也表明从低到高的波动状态的过渡发生在很短的一段时间。

2008年6月以来，CDS市场上受次贷危机的影响不断加深，金融危机影响背后存在许多结构性和技术性的因素冲击着香港CDS市场，并导致CDS价格指数剧烈波动，结合当时香港市场的实际情况，这些因素主要包括以下方面：

第一，政策制定者非常担忧CDS价格的上升可能导致卖家的自利性保护，造成没有足够的储备来支付未来的索赔，违约的一方在整个金融系统中可能会导致一连串的问题。

第二，当CDS保护的抵押贷款所支持的证券于2008年开始失去价值时，投资者开始担心CDS市场可能突然面临着巨大的负债及风险。

第三，自2009年夏季以来的债务抵押债券（CDO）市场已明显转弱，导致销售与合成CDO及相关产品连接的保护需求下降。

第四，香港CDS市场投资者买卖保险以防止债券市场上的违约行为，当投资者越来越关心企业的生存能力时，相应的保护成本则会上升。

第五，诸如第n期违约掉期结构性产品的损失，由多个企业信贷构成的CDS被频繁使用，对其损失信用保障需求有了很大的增加，故需要通过反向交易进行对冲平仓。

五、结 论

前几年的次贷危机所诱发的金融危机对金融市场造成了强大的冲击，引发了整个银行业的危机和持续的信贷紧缩，造成全球经济增长的减速。基于此，本文剖析了违约风险溢价的变化对股市状况的灵敏度以及通过使用马尔可夫转换模型的两个状态来剖析宏观经济变量与信贷违约上升及非经济危机之间的关系，针对HSI CDS指数利差为代表的违约风险溢价问题，通过马尔可夫转换模型研究了香港HSI CDS指数的马尔可夫转换过程，分析了敏感股指波动与金融危机期间的工业生产指数等宏观经济变量的关系，揭示了在金融危机期间的信用违约风险溢价、股市波动与宏观经济变量的内在联动性，进而对违约风险溢价的深层次问题进行了深入研究和探讨。

［1］ Hsu J C，Santa Clara P．Bond Pricing With Default Risk［C］．Working Paper，Anderson School，UCLA，2002．

［2］ Collin Dufresne P，Goldstein R S，Martin J S．The Determinants of Credit Spread Changes［J］．Journal of Finance，2001（8）．

［3］ Lando D．On Cox Process and Credit Risky Securities［J］．Review of Derivatives Research，1998（2）．

［4］ Duffee G．Estimating the Price of Default Risk［J］．Review of Financial Studies，1999（6）．

［5］ Longstaff F A，Mithal S，Neis E．Corporate Yield Spreads：Default Risk or Liquidity？New Evidence From the Credit Default Swap Market［J］．Journal of Finance，2005（5）．

［6］ Elton E J，Gruber M J，Agrawal D，Mann C．Explaining the Rate Spread on Corporate Bonds［J］．Journal of Finance，2001（1）．

［7］ Blanco R，Brennan S，Marsh I W．An Empirical Analysis of the Dynamic Relation Between Investment－grade Bonds and Credit Default Swaps［J］．Journal of Finance，2005（5）．

［8］ Dupuis D，Jacquier E，Papageorgiou N，Rémillard B．Empirical Evidence on the Dependence of Credit Default Swaps and Equity Prices［J］．Journal of Futures Markets，2009（8）．

［9］ Friedman B，Kuttner K．Indicator Properties of the Paper－bill Spread：Lessons From Recent Experience［J］．Review of Economics and Statistics，1998（11）．

［10］Stokes H H，Neuburger H M．New Methods in Financial Modeling：Explorations and Applications［M］．Westport，CT：Quorum Books，1998．

［11］Ewing B T．The Response of the Default Risk Premium to Macroeconomic Shocks ［J］．The Quarterly Review of Economics and Finance，2003（5）．

［12］Estrella A．Predicting US Recessions：Financial Variables as Leading Indicators［J］．Review of Economics and Statistics，1998（1）．

［13］Tang D Y．Macroeconomic Conditions，Firm Characteristics，and Credit Spread ［J］．Journal of Financial Services Research，2006（3）．

［14］Duffie D，Saita L，Wang K．Multi－Period Corporate Default Prediction with Stochastic Covariates ［J］．Journal of Financial Economics，2007（5）．

［15］Gharghori P，Chan H，Faff F．Default Risk and Equity Returns：Australian Evidence［J］．Pacific－Basin Finance Journal，2009（9）．

［16］Hamilton J D．A New Approach to the Economic Analysis of Nonstationary Time Series and the Business Cycle［J］．Econometrica，1989（2）．

［17］丁东洋，周丽莉．基于贝叶斯方法的信用评级模型构建与违约概率估计［J］．统计与信息论坛，2010（9）．

［18］Dooley M，Hutchison M．Transmission of the U．S．Subprime Crisis to Emerging Markets：Evidence on the Decoupling－Recoupling Hypothesis［J］．Journal of International Money and Finance，2009（12）．