基于q－高斯分布的投资组合实证分析

刘遵雄，刘江伟，郑淑娟，陈 英

（1．华东交通大学 信息工程学院，江西 南昌330013；2．江西财经大学 科研处，江西 南昌330013）

一、引 言

一般分布已经不能满足复杂系统和交叉学科的研究要求，自从Tsallis提出q－分布以来，q－分布理论已经得到广泛研究并且成功应用于各种复杂系统中［1］。q－高斯分布是q－分布家族中重要的一员，实质上可以看作是在约束条件下Tsallis熵最大化而得到的一种概率密度函数，亦可以看作是一种广义高斯分布［2］。q－高斯分布可以由多种模型或随机微分方程推导出来，而且表达形式也稍有差异。其中由线性随机微分方程推导出的密度函数表达形式易于理解和应用，参数对分布的影响也很直观［3－4］。q－高斯分布比高斯分布更加灵活，其参数可以灵活地控制其尖峰厚尾分布，这对研究具有尖峰厚尾分布特性的金融时间序列有重要意义。

为了研究方便，学者们在研究金融市场股票收益率时通常假设其服从正态分布，然而从统计检验结果来看，股票收益率并不能很好的服从正态分布，再加上人们对金融市场的分析结果要求越来越严格，因此在研究如何改进金融模型时，改进其分布假设成为一个重要的研究方向。随着全球经济一体化进程的加快和中国金融市场的发展与完善，中国金融机构对投资组合理论的应用实践提出了具体要求。投资组合理论主要研究投资者如何利用分散投资来优化他们的投资组合，在最小风险的期望下获得最大的收益［5］。经典的投资组合模型包括均值－方差模型和均值－VaR模型［6－7］。虽然以期望度量收益，方差度量风险的均值－方差模型被广泛应用于资产组合优化，然而由于方差作为度量测度具有“对称”性，即在最小化方差的同时，也限制了可能的收益。VaR作为一种简便、易于理解的风险度量方法，代替方差作为均值－方差模型的风险度量，构成了均值－VaR模型，成为目前流行的资产组合优化模型。

考虑到股票收益率分布的尖峰厚尾特性，本文将q－高斯分布引入到投资组合模型中，并和基于高斯分布的投资组合模型进行了实证比较，结果表明，基于q－高斯分布假设的投资组合模型具有更高的风险预测能力，并能带来较大的收益。

二、q－高斯分布

（一）q－高斯分布密度函数的推导

已有研究表明，可以利用不同的随机微分方程或模型推导出q－高斯分布密度函数，如非线性随机微分方程，马尔科夫转换模型，带有卡方分布的高斯处理过程，有噪声的线性随机微分方程等［8－10］［3］。本文从含有噪声的线性随机微分方程出发，推导出q－高斯分布概率密度函数的表达形式。含有白噪声的一种线性随机微分方程可以表示为：

为便于求解，将式（1）写成伊藤福克尔－普朗克方程（Ito－Stratonovich Fokker－Planck equation）的形式：

其中β＞0，q＞1。

随机变量为N维情况时，含有噪声的线性随机微分方程根据式（1）可以写成：

（二）q－高斯分布的参数估计

多元q－高斯分布的概率密度函数表达式中，需要估计的参数有正交矩阵Q，形状参数βj，qj。q－高斯分布的参数估计方法很多，有矩估计法、最大似然估计法、曲线拟合参数估计方法等。下面以矩估计法为例，给出q－高斯分布概率密度函数的参数估计方法。

首先根据抽样方法，计算样本协方差Sspl，估算总体协方差S，对S做对角化运算，根据QSQ＇＝diag（λ1，λ1，…，λ1）求出Q。

（三）参数对q－高斯分布的影响

为能直观地考察q－高斯密度函数中参数对分布的影响，以二元q－高斯函数为例进行研究。由式（13）知，二元q－高斯的密度函数为：

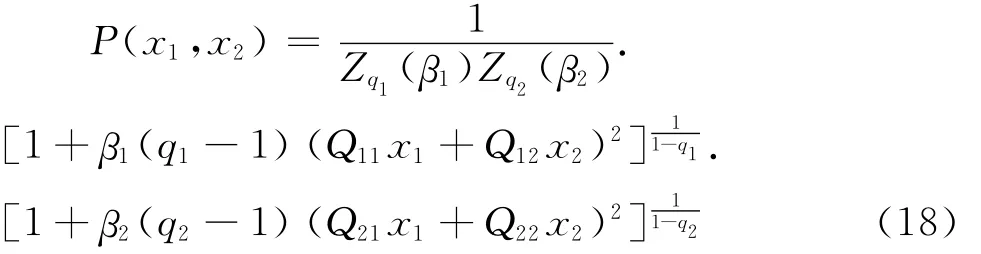
其中Q为单位正交矩阵，β1＞0，β2＞0，1＜q1＜3，1＜q2＜3。根据启发式算法思想，选取不同的q，β画出二元q－高斯分布的图形以便比较参数对分布的影响，可以得到如下两条结论：第一，选取β1＝β2＝1，Q＝ ［1，0；0，1］不变，q1＝q2分别取2．9，2．2，1．6，1．1，观察其分布图形和垂直截面图可以看出，当β，Q不变，q越小时，图形越尖；第二，选取q1＝q2＝2，Q＝［1，0；0，1］不变，β1＝β2分别取1，2，5，10，观察其分布图形和垂直截面图可以看出，当q，Q不变，β越大时，图形越尖。考虑到金融市场股票收益率分布的尖峰厚尾性，可以通过调整q－高斯分布密度函数中的参数，更加准确地拟合收益率的分布，这为研究股票收益率提供了更好的统计分析工具。

三、投资组合模型

（一）均值－方差模型

Markowitz投资组合理论认为，投资者进行决策时，总希望以尽可能小的风险获得尽可能大的收益，或在收益率一定的情况下，尽可能降低风险［11］，因此现代投资组合理论主要研究投资者如何利用分散投资来优化他们的投资组合比例。Markowitz均值－方差模型，是用于估计投资者投资组合风险与收益的一种有力的工具［6，12］。假设有n个资产，他们的收益率分别为R1，R2，…，Rn，用向量表示为R＝（R1，R2，…，Rn），其均值为μ＝（μ1，μ2，…，μn），协方差为 Σ（n阶 方 阵），Ri、Rj的 协 方 差 记 为 cov（Ri，Rj），向量w＝ （w1，w2，…，wn）T为投资组合的投资比例，则Markowitz均值－方差模型形式化地表示为：

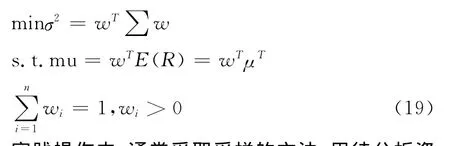
实践操作中，通常采取采样的方法，用待分析资产收益率数据的均值和方差S来估计整体均值和方差，即：

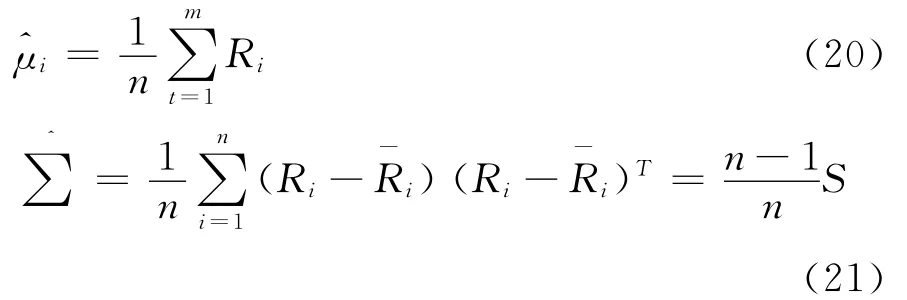
（二）均值－VaR模型

均值－方差模型利用收益率的方差作为风险测度，这种方法虽然可以有效的减小组合收益的波动，但由于方差是一种“对称”的度量，方差的最小化不只会减少收益向下的偏离，同时也会减少收益向上的偏离，所以它同时也限制了可能的收益［5］。VaR（Value at Risk）指的是在正常的市场条件中，在一定持有期及置信水平下，某一资产或投资组合所面临的最大的损失［13］。用VaR代替方差作为风险的测度就得到了均值－VaR模型［7］，可以形式化地表示成如下形式：

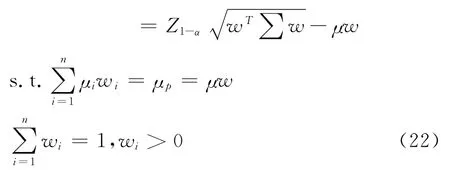
相关研究表明，约束条件下均值－VaR的有效解集是均值－方差有效解集的子集，且均值－VaR的最优解为［5］：

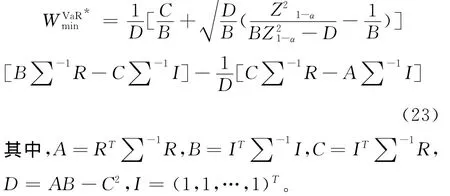
四、实证分析

一般情况下，均值－方差模型和均值－VaR模型都是在高斯分布假设下对投资比例进行估算，为了获得更优的投资比例，本文将对实际的收益率数据进行统计检验并验证将q－高斯分布应用于该投资组合模型的有效性。选取沪市三只股票（海信电器HXDQ600060，三一重工SYZG600031，同方股份TFGF600100），选取2011年6月2日到2012年12月31日共388个日收益率数据（数据来源：锐思数据库http：／／www．resset．cn／cn），其基本检验统计量如表1所示。

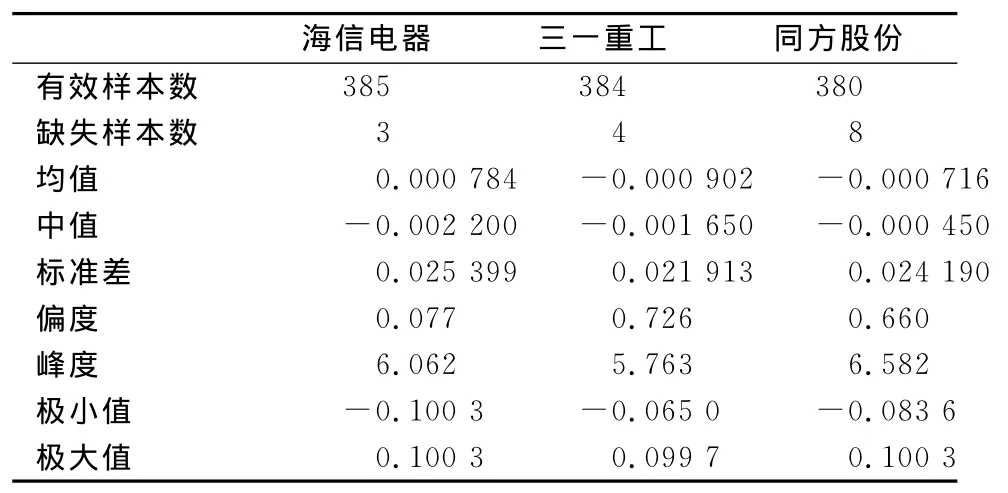
表1 频率检验统计量表

从表1知，三支股票峰度分别为6．062，5．753，6．582，均大于标准正态分布的峰度值3，说明三只股票不服从标准正态分布。卡方检验和QQ图检验的结果也说明三支股票不服从标准正态分布。绘制出三只股票的直方图，分别用正态分布（均值方差参数见表1）和q－高斯分布拟合三只股票的收益率分布如图1－3所示（其中计算出来的q－高斯分布的参数分别为βHXDQ＝907，qHXDQ＝1．214 8；βSYZG＝1 462．3，qSYZG＝1．269 7；βTFGF＝3 111，qTFGF＝1．307 8）。从图上可以看出，q－高斯拟合曲线比高斯曲线有更高的尖峰，更厚的尾部，更接近收益率数据的实际分布，说明用q－高斯分布拟合收益率分布的效果更好。

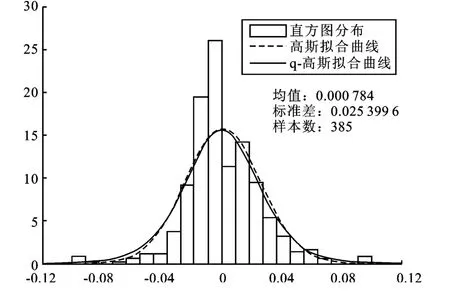
图1 海信电器直方图及拟合曲线图

图2 三一重工直方图及拟合曲线图

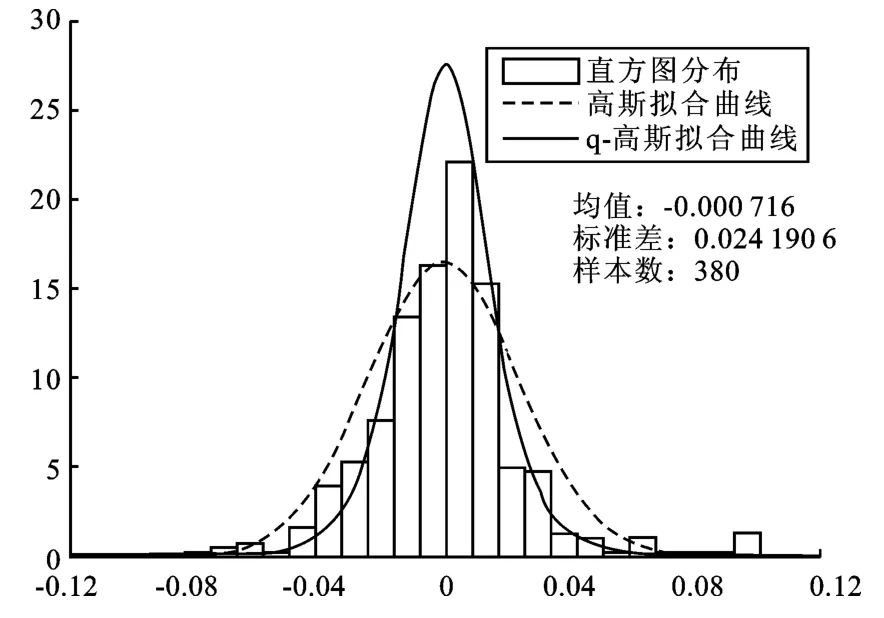
图3 同方股份直方图及拟合曲线图

分别用高斯分布和q－高斯分布拟合三只股票的收益率分布，采用均值－方差模型和均值－VaR模型分别解出该模型所对应的投资比例见表2，并同时画出均值－方差模型和均值－VaR模型有效前沿如图4所示。从图4可以也可以看出，均值－VaR模型的解是约束条件下均值－方差模型的有效子集。用计算出来的投资比例投资于所选三只股票，用2013年1月4日到2013年1月31日的收益率数据做实证比较，实际收益如表2中“实际收益”所示。

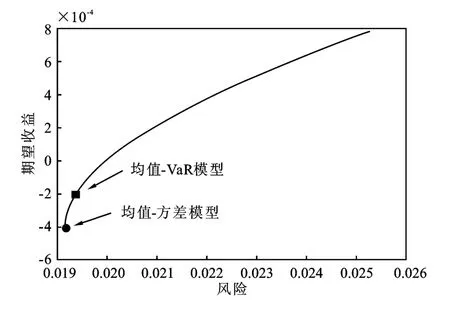
图4 均值－方差和均值－VaR模型有效前沿图

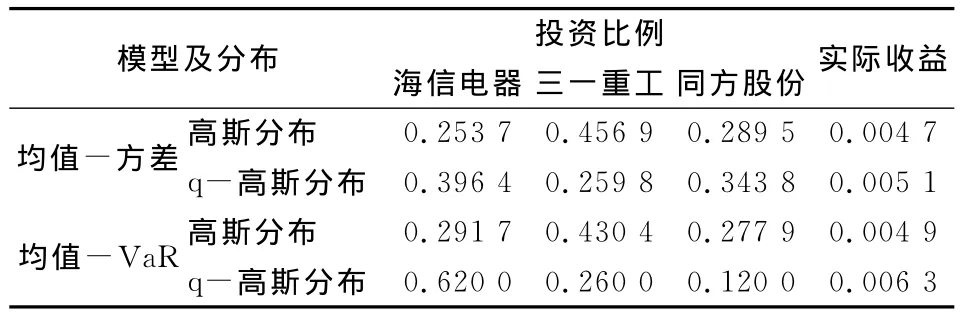
表2 不同分布假设下投资组合模型的投资比例与实际收益表

从表2可以看出，基于q－高斯分布的均值－方差模型投资比例为［0．396 4，0．259 8，0．343 8］，实际收益为0．005 1，大于高斯分布假设下的0．004 7；基于q－高斯分布的均值－VaR模型投资比例为［0．620，0．260，0．120］，实际收益为0．006 3，同样大于高斯分布假设下的0．004 9；并且基于q－高斯分布的均值－VaR模型是表2中四种模型中最优的。实证结果表明将q－高斯分布应用于投资组合模型中，可以提高模型解的有效性，同时基于此解做投资，可以有效提高预期收益。

五、结 论

本文从含有白噪声的线性随机微分方程中推导了q－高斯分布密度函数的表达式，并研究了其尖峰厚尾的特性。考虑到通常股票收益率分布具有尖峰厚尾特性，因此将q－高斯分布应用于投资组合理论的均值－方差模型和均值－VaR模型。选取沪市三支股票进行实证分析和求解，并与基于高斯分布假设下的求解做了比较，结果表明将q－高斯分布应用于投资组合模型可以更准确的拟合收益率的分布，并且按照基于q－高斯分布的投资组合模型的投资比例选择股票，可以带来更多实际收益。

［1］ Vignat C，Plastino A．Why is the Detection of q－Gaussian Behavior Such a Common Occurrence？［J］．Physica A：Statistical Mechanics and its Applications，2009，388（5）．

［2］ Ghoshdastidar D，Dukkipati A，Bhatnagar S．q－Gaussian Based Smoothed Functional Algorithms for Stochastic Optimization［C］．Cambridge：IEEE International Symposium on Information Theory Proceedings，2012．

［3］ Sato A，Takayasu H，Sawada Y．Power Law Fluctuation Generator Based on Analog Electrical Circuit［J］．Fractals，2000，8（3）．

［4］ 刘君．多元q－高斯分布在投资组合模型中的应用［D］．武汉：武汉理工大学硕士学位论文，2012．

［5］ 荣喜民，武丹丹，张奎廷．基于均值－VaR的投资组合最优化［J］．数理统计与管理，2005（5）．

［6］ Fabozzi F J，Markowitz H M，Kolm P N，et al．Mean－Variance Model for Portfolio Selection［M］．New York：John Wiley ＆Sons，Inc．，2012．

［7］ Baixauli－Soler J S，Alfaro－Cid E，Fernandez－Blanco M．Mean－VaR Portfolio Selection Under Real Constraints［J］．Computational Economics，2011，37（2）．

［8］ Kaulakys B，Ruseckas J，Gontis V，et al．Nonlinear Stochastic Models of Noise and Power－law Distributions［J］．Physica A：Statistical Mechanics and Its Applications，2006，365（1）．

［9］ Timmermann A．Moments of Markov Switching Models［J］．Journal of Econometrics，2000，96（1）．

［10］Beck C，Cohen E G D．Superstatistics［J］．Physica A：Statistical Mechanics and Its Applications，2003（322）．

［11］孟勇．Markowitz模型与Black－Litterman模型比较研究——投资人情绪对资产组合的影响［J］．统计与信息论坛，2013，28（8）．

［12］Fontana C，Schweizer M．Simplified Mean－Variance Portfolio Optimisation［J］．Mathematics and Financial Economics，2012，6（2）．

［13］Daníelsson J，Jorgensen B N，Samorodnitsky G，et al．Fat Tails，VaR and Subadditivity［J］．Journal of Econometrics，2013，172（2）．