基于ANSYS的小型赛车车架的有限元分析
马泽宏, 纪飞, 傅蔡安
(江南大学 机械工程学院,无锡214122)
1 引 言
FSAE 大学生方程式(Formula SAE,FSAE)汽车大赛旨在由学生自主构思,设计和制造出符合规则的赛车来参加比赛。参赛车辆将在一系列的静态和动态项目中进行测评,其中包括:技术检查、制造成本分析、营销报告、赛车设计、单项性能测试和良好的赛道耐久性。
2 车架设计
车架是FSAE 赛车的重要组成部分,车架设计的一般步骤是车架形式的选择、空间结构的设计、钢管规格的选择以及验证是否符合人机工程学。为了减轻车架的重量,车架采用了不同壁厚的圆管,当然,这都是在满足车架拥有一定的强度并且符合规则的前提下。车架的设计主要用CATIA 软件零件设计模块完成,然后使用塑料管搭建出1∶1 的模型以验证是否符合人机工程学并进行优化。FSAE 赛车车架CATIA 模型见图1。

图1 FSAE 赛车车架CATIA 模型
3 有限元模型的建立
首先在ANSYS Workbench 中建立一个静态结构分析流程,利用ANSYS 中CATIA 接口,将在CATIA 里建立三维模型导入到ANSYS 中。
导入的几何模型可能会有一些重复的单元,对其进行一些清理后,采用默认的设置,对车架进行网格划分,划分的结果如图2 所示。
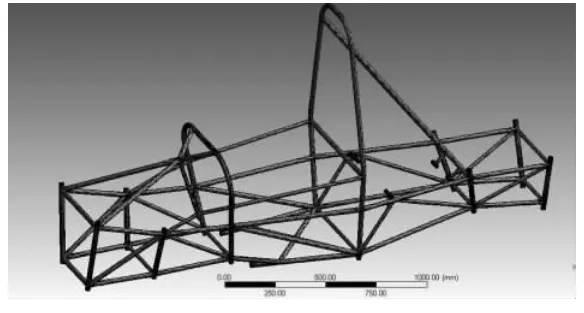
图2 车架的网格划分
4 车架刚度分析
划分完网格后,就可以对车架进行受力分析。参考国内外FSAE 车队的资料,对四种工况下车架进行有限元分析,分别为弯曲、制动、转弯和扭转工况。发动机重量为60kg,车手重量取60kg,刹车系统部件取5kg,后轮传动部件取10kg。
4.1 弯曲工况
赛车匀速行驶在水平路面上的受力情况为弯曲工况,车架主要受到车手、发动机和其它零部件在竖直方向上的力。
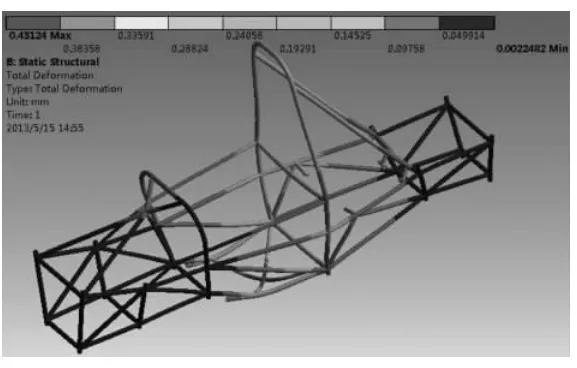
图3 弯曲工况车架变形图
有限元分析时,需要为车架所承受的载荷乘以一个动载系数(一般不超过3.0),因为路面状况良好,我们取动载系数为2.0。车架所受的静载荷主要来自于车架自重、车手重量、发动机重量和零部件的重量,进行有限元分析时,这些力通过相应节点作用在车架上。设置好边界条件后,就可以进行分析,分析结果如图3 所示。
从分析结果可知,车架最大变形发生在座椅与车架连接的地方,为0.43mm,其次主环与主环斜撑也出现了0.2mm 左右的变形。车架最大应力也是出现在座椅与车架连接处,最大应力为33.6MPa,远小于4130 铬钼钢的屈服极限(485MPa)。因此,车架强度满足要求。
4.2 制动工况
赛车在紧急制动时,车架除受与弯曲载荷一样的赛车自重外,同时受制动产生的惯性力的作用,车架内部应力也发生变化,并发生轴荷转移。假设赛车以1.4×9.8m/s2的加速度制动,并取1.5 倍动载因数,受力分析时,在发动机、座椅与车架连接处施加大小为1260N,方向沿-X 方向,在车架上施加1.4×9.8m/s2的纵向加速度来模拟赛车紧急制动时车架承受载荷情况。分析结果如图4 所示。
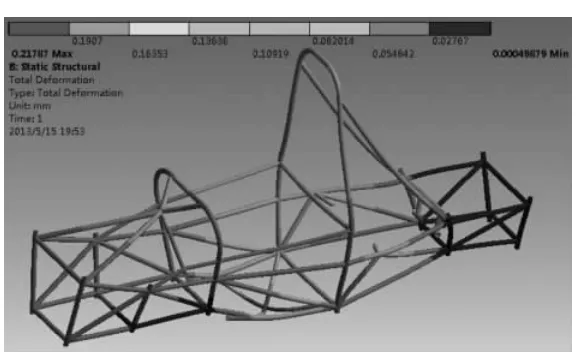
图4 制动工况车架变形图
从上述分析结果可知,车架最大变形为0.21mm,发生在发动机、座椅与车架连接处。主环和其斜撑变形量均较小。车架最大应力为29.3MPa,出现在发动机、座椅与车架连接处,但是其值远小于4130铬钼钢的屈服应力(485MPa),故可知制动工况下车架强度符合要求。
4.3 转弯工况
比赛中经常会出现赛车高速过弯的情况,因此需要对高速转弯工况进行校核。紧急转弯时,车架将会因为离心力而承受侧向载荷,本文模拟赛车以1.4×9.8m/s2向心加速度过弯,动载因数取1.5,受力分析时,在发动机、座椅与车架连接处施加大小为1260N,方向沿Y 方向。在车架上施加1.4×9.8m/s2的横向加速度来模拟赛车高速右转弯时车架承受载荷情况,分析结果如图5 所示。
从上述分析结果可知,车架最大变形为2.4mm,发生在主环顶端。前环顶端变形量为2.1mm 左右,其余部分变形较小,均小于1mm。车架最大应力为77.3MPa,出现在车架底部与座椅连接处,但是其值远小于4130 铬钼钢的屈服应力(485MPa),故可知转弯工况下车架强度符合要求。
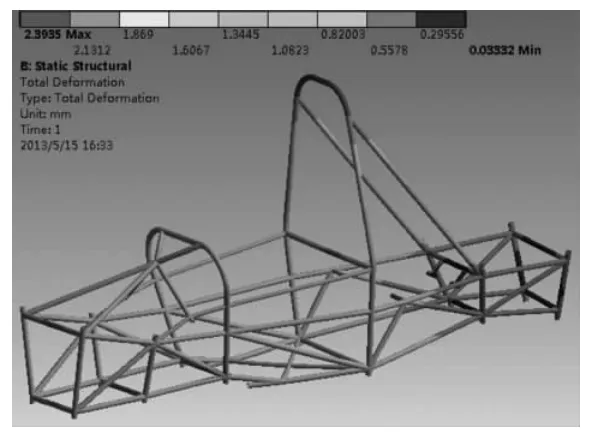
图5 转弯工况车架变形图
4.4 扭转工况
扭转工况是指赛车在转弯或者遇到不平路面时,四个轮子不在同一个平面而使车架产生扭转弯曲。而车架结构的抗扭转刚度对整部赛车的性能发挥影响较大,因此有必要对车架的扭转工况进行分析。赛车满载时前轴荷为110kg,动载系数取1.5,分别在前轴所在位置对应车架的最下端加载,分别加载±825N。分析结果如图6 所示。
从上述分析可知,车架最大变形发生在前环处,为0.34mm,其余部分均较小。车架最大应力出现在悬架与车架铰接点处,值为72.3MPa,远小于4130 铬钼钢的屈服应力(485MPa),故可知车架扭转工况强度满足要求。
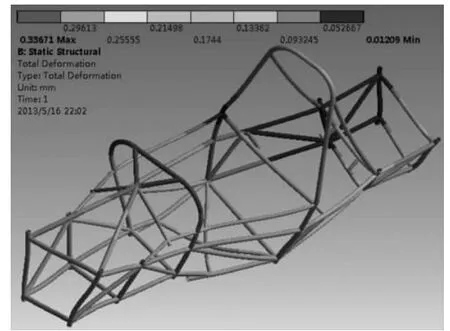
图6 扭转工况车架变形图
5 车架模态分析
赛车在赛道行驶的过程中,会因为路面的不平整、车轮动态不平衡、发动机的振动而产生随机的激振。为了避免车架因为共振而产生破坏,就要使车架的固有频率避开激振的频率。本文通过对车架的固有振动频率和振型的分析,并对车架的结构进行必要的调整。
赛车不平的路面上行驶所引起的激励频率多集中在5~20Hz,因车轮不平衡引起的激振频率一般低于11Hz。根据爆发频率计算公式
f=2in/60τ
其中,f 为激振频率;τ 为 冲 程;i 为缸数;n 为发 动机的转速。
对于我们所选用的本田CBR600发动机,i=4,τ=4,n=3000r/min,因此计算出发动机的爆发频率为100Hz。在进行车架设计时,为避免发生共振,要使车架的低阶频率介于路面激励和发动机爆发频率之间。
在ANSYS 中建立一个模态分析流程,其与静态结构分析共用有限元模型,设置模态阶数为6,寻找范围为0~200Hz(图7)。求解完成后,对每一阶绘出变形结果图,通过对车架模型进行模态分析,得到车架在侧向扭转、弯扭组合、侧向弯曲、弯扭组合等情况下的振动频率和振型,如图8~图13 和表1 所示。
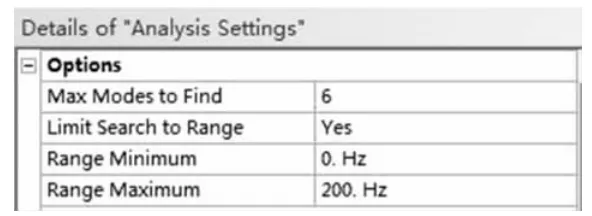
图7 参数设置

图8 侧向扭转
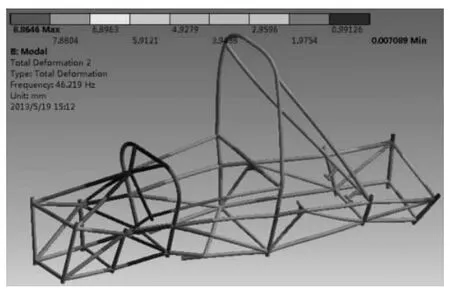
图9 弯扭组合

图10 侧向弯曲

图11 弯扭组合
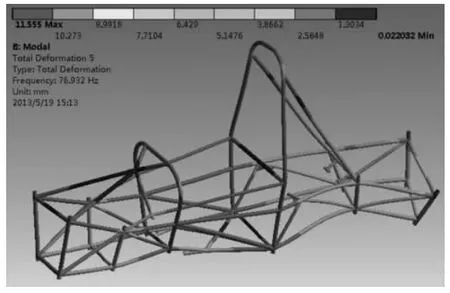
图12 弯扭组合
从上述分析可以看到,该车架结构的前6 阶固有频率在32.348~80.068Hz 之间,低阶模态大于20Hz,高阶模态小于100Hz,这样就在很大程度上避免了共振。所以,车架的设计是满足要求的。

图13 弯曲振型
6 结 语
本文在简单介绍模态分析理论的基础上,在ANSYS 中建立模态分析流程,让其与静态结构分析共享有限元模型,这样就省去了重新建立有限元模型的步骤。设置分析参数后,通过对车架模型进行模态分析,得到了车架的前6 阶模态,从分析结果可以得出车架的动态特性较为理想的结论。
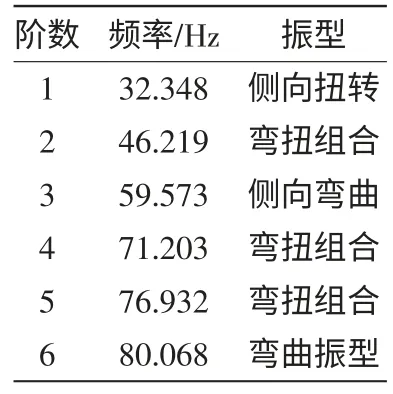
表1 车架前六阶固有频率及振型
[1] 2013FSC 油车规则(公示版)[Z].北京:中国汽车工程协会,2013.
[2] MILLIKEN W F,et al. Race Car Vehicle Dynamics[M].Warrendale,PA:SAE International,1995.
[3] EDMUND F,et al. Introduction to Formula SAE? Suspension and Frame Design[R]. PA:SAE International,1997.
[4] 王望予.汽车设计[M].北京:机械工业出版社,2006.
[5] 刘松涛,刘云龙,吴宁宁,等.天津大学2010 年赛车设计报告[R].上海:中国汽车工程学会,2010:3-28.
[6] 李嫚.FSAE 赛车悬架的优化设计及分析[D].哈尔滨:哈尔滨工业大学,2010.
[7] 王家豪.FSAE 管阵式车体骨架结构设计与分析[D].广州:华南理工大学,2010.
[8] 邝坤阳.FSAE 赛车车架的结构分析与优化[D].合肥:合肥工业大学,2009.
[9] 居小凡.Formula SAE 赛车的设计制造及测试[D].上海:上海交通大学,2009.
[10] 姜胜男.悬架测试试验台的研究[D].长春:长春理工大学,2006.
[11] 刘美燕.FSAE 赛车悬架仿真分析及操纵稳定性虚拟试验[D].长沙:湖南大学,2008.
[12] 刘晨曦.FSAE 大学生方程式赛车操纵稳定性的研究[D].合肥:合肥工业大学,2011.
[13] 吕亚云.旋喷泵的振动特性分析与研究[D].镇江:江苏大学,2011.
[14] 杨红平,等.基于有限元法对结合面实验箱模态分析研究[J].天水师范学院学报,2010(2):82-84.
[15] RILEY W B,GEORGE A R. Design,analysis and testing of a formula SAE car chassis [C]//Motor sports Eng Conf &Exhibition,Indianapolis,2002:382-399.

