基于CORDIC算法的线性调频信号产生*

朱双兵，杨维明，吴 恙，胡 晶

(湖北大学物理学与电子技术学院，武汉430062)

线性调频信号，又称为chirp信号，其突出优点是对多普勒频移不敏感，即具有较大频移的回波信号通过匹配滤波器后仍能得到较好的脉冲压缩性能，并且输出响应会出现与多普勒频移成正比的附加时延，利用这一特性可以简化信号处理系统的设计［1］。

在通信、雷达和导航系统中高精度的DDS有着广泛的应用。近年来随着电子技术的迅速发展，传统的查表、多项式展开或近似实现DDS的方法需占用较多的存储单元、高精度乘法运算需花费较多的运算时间，不适应现代电子系统在速度、精度和集成度实现方面的要求，而采用CORDIC［2］算法(坐标旋转数字计算机算法)实现的DDS系统不需要查表、以移位和加法运算代替乘法运算，便于软硬件实现，能满足高性能系统的设计要求，因此受到人们的广泛关注［3］。但现有文献大多仅从理论上对CORDIC算法进行了分析与仿真，缺乏基于该算法的硬件实现报道。

本文分析了CORDIC算法的原理，研究了该算法的硬件设计与实现方法，将调制后的相位进行CORDIC算法处理后获得线性调频信号，通过在ModelSim上进行RTL仿真，结果表明本设计方法是完全可行的。

1 线性调频信号

1.1 线性调频信号的时域特性

线性调频信号LFM的信号频率对时间的导数为常数［4］:

f(t)为瞬时频率，u为调频斜率，则相应瞬时相位函数为:

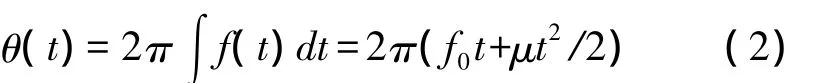
时间宽度T的复数信号为:

其中u(t)为信号复包络，u=B/T为频率变化率，B为信号频率，T为信号时间宽度，f0为信号的中心频率。若令f0=0，得到零中频信号即基带信号，而复信号的实部和虚部则分别构成两路正交信号。

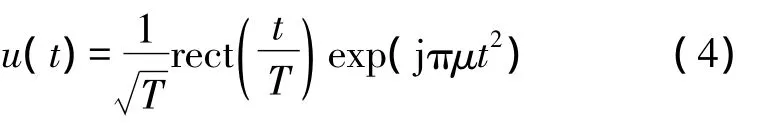
图1给出了B=20 MHz，T=10 μs的 LFM 信号基带波形。

图1 LFM的实部和虚部

1.2 线性调频信号的相位调制

根据上述线性调频信号的相位调制函数，可以得出相位与时钟之间的数学关系，在本设计中的时钟频率为50 MHz，即时钟周期为20 ns。调频信号的带宽为B=20 MHz，脉冲宽度为T=10 μs，故可得频率变化率为u=B/T=2×1012，瞬时相位(基带信号)为:

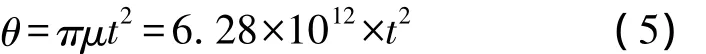
将连续时间t离散化:t=n×20 ns(其中n=0，1，2，3…表示时钟周期的个数)，则有:

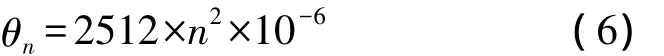
使用Verilog硬件描述语言在FPGA上实现相位调制时，运用有符号数的乘法即可实现。

2 CORDIC算法的原理与实现

CORDIC(坐标旋转)算法的基本思想是:若要将一平面向量旋转θ°，可以将此角度值分解成一系列基本角度，以这些基本角度值对向量进行多次小角度旋转，最终逼近角度θ。该算法的巧妙之处在于基本角度的选取恰好使得每次旋转后，使中间向量的坐标值可以用简单的移位和加减法操作得到。由于需要经过多次旋转以逼近角度θ，因而CORDIC算法是一种迭代算法。

2.1 CORDIC的旋转模式

假设直角坐标系内有一初始向量OA1逆时针旋转角度θ后到目标向量OA2，如图2所示。

图2 CORDIC算法原理图

用坐标可表示为:

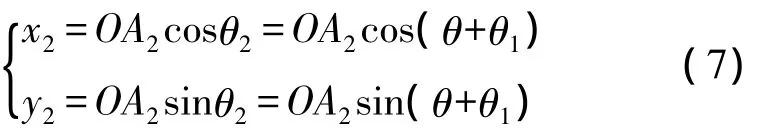
将上式展开有:

并用矩阵形式可表示如下:

若将OA1旋转到OA2的过程分成n次旋转，其中第i次旋转角度为θi，那么第i次旋转的表达式为:

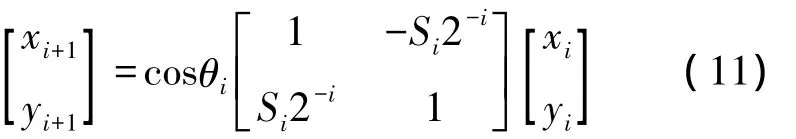
式中cosθi=cos(arctan(2-i))。随着旋转次数的增加(本设计共旋转15次)，该式收敛为一个常数:

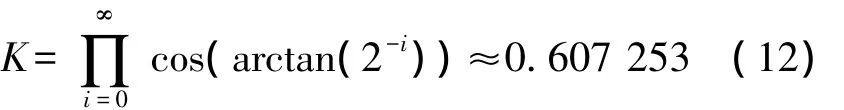
2.2CORDIC算法实现DDS

本文使用CORDIC算法来产生正弦和余弦信号，采用Verilog硬件描述语言［6］实现15级流水线结构［7］。

设初始向量坐标为(x0，y0)，与目标向量(xn，yn)的夹角为z0。这里用zi表示第i次旋转后与目标角度之差，则有:

其中zi大于0时，Si=+1;zi小于0时，Si=-1;zi等于0时，Si=0。经过n次旋转以后得到以下结果［8］:

式中，x0，y0，z0为初始值，如果取x0=K，y0=0，z0=θ则迭代结果为:

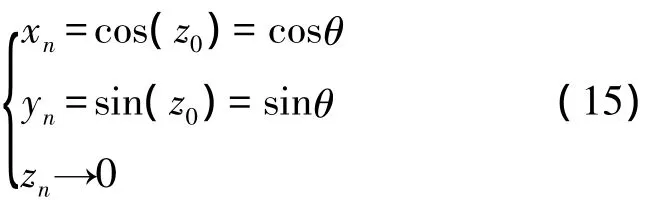
所以将角度值(z0)输入，最后的迭代结果xn和yn就是需角度θ的余弦和正弦值，在式(13)的迭代公式中，由于乘以2-i相当于被乘数右移i位，因此乘法运算在电路实现时可以简化为移位运算，因此只需要加减法和移位运算即可实现CORDIC算法。

每次旋转的角度值是固定的，即2-i的反正切，将此角度值预先算出，根据流水线的级数直接调用相应旋转角度的值，相应Verilog代码如下:

在旋转过程中需要对角度的反正切进行移位操作，而在移位过程中必须保证移位结果的正确性，特别是负数的移位操作，而对于Verilog中有数据的算术移位操作(＞＞＞)，在计算过程中会出错，例如在计算0度的正弦时，第八级流水线单元的输入为Xi=32 767，Yi=-25，经计算后输出为Xo=32 767-(-25＞＞＞7)，其理论结果应仍为Xo=32 767，即-25右移7位后结果应为零，但算术移位运算对-25操作后并不为零，由此算出的Xo溢出，导致后续流水单元相继出错。改进算法通过判断输入符号位，当符号位为1，即负数时，先对输入取反加1后再逻辑右移相应位数，然后将右移后的结果取反加1，即可正确快速地实现负数移位操作;当符号位为0，则直接进行逻辑右移。Verilog移位操作函数如下:

15级流水线的CORDIC算法模块经QuartusⅡ综合后的RTL如图3所示。其中每一级单元如图4所示。

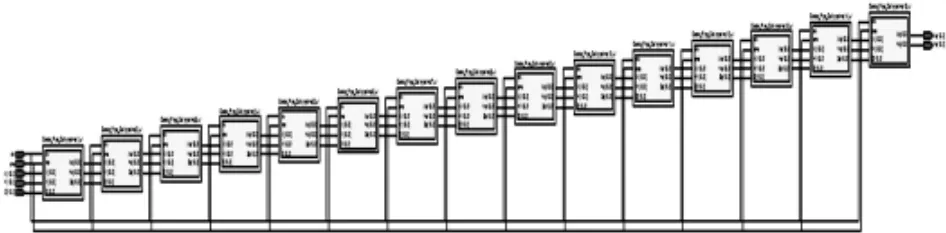
图3 流水线结构的CORDIC算法RTL图

图4 每一级流水线单元

在输入端输入相应的相角值即可算出相应的正弦和余弦幅值。在本设计中相角输入为20位宽度，则1度对应的相角值为:

使用CORDIC算法产生正余弦信号的RTL仿真结果如图5所示。

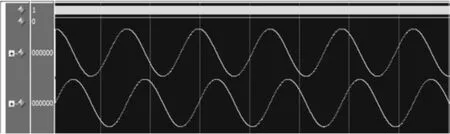
图5 CORDIC算法实现DDS波形

3 线性调频信号的产生

在上节中的DDS模块输入线性调频信号的已调制相位后，即可得出线性调频信号。首先需要相位调制模块，本设计中时钟频率为50 MHz，根据1.2节中相位与时钟之间的关系:θn=2 512×n2×10-6，通过时钟计数后得出瞬时相位。

由此得到的相位还需要进行相位映射，因为CORDIC的输入范围(经15次旋转的角度之和)为:98.883°～+98.883°，这里将调制后的相位θn映射-在-90°～ +90°范围内。当0°≤θn≤90°，相位值不变;当90°＜θn≤180°时，相位值映射到第一象限为(180-θn)即0°＜θn≤90°;当180°＜θn≤270°，相位值映射到第四象限为(180°-θn)即-90°≤θn＜0°;当 270°＜θn≤360°，相位值映射到第四象限为(θn-360。)即-90°＜θn≤0°。象限的映射转换如图6所示。

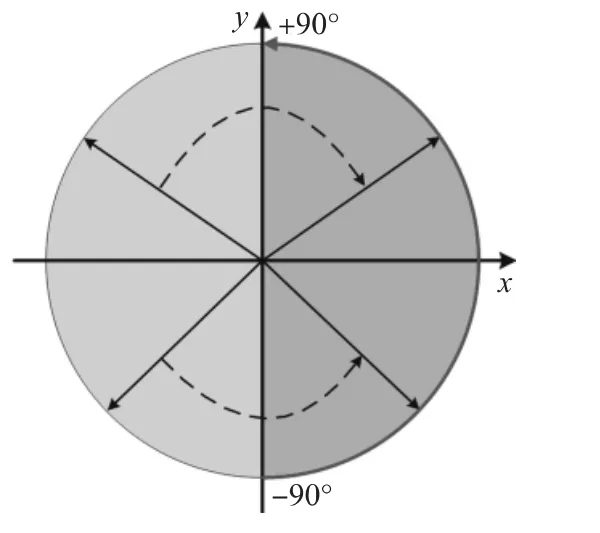
图6 象限映射转换图

象限映射后，在整个2π周期内的相位都可以通过CORDIC模块得出正确的正弦和余弦值。而在-90°～+90°范围内，余弦输出只能为正，所以当90°＜θn≤270°时，还需将 CORDIC 的余弦输出值求反。将线性调制后的相位先映射至CORDIC的输入范围内，即可输出线性调频信号。整个工程在QuartusⅡ中综合得出的RTL如图7所示。

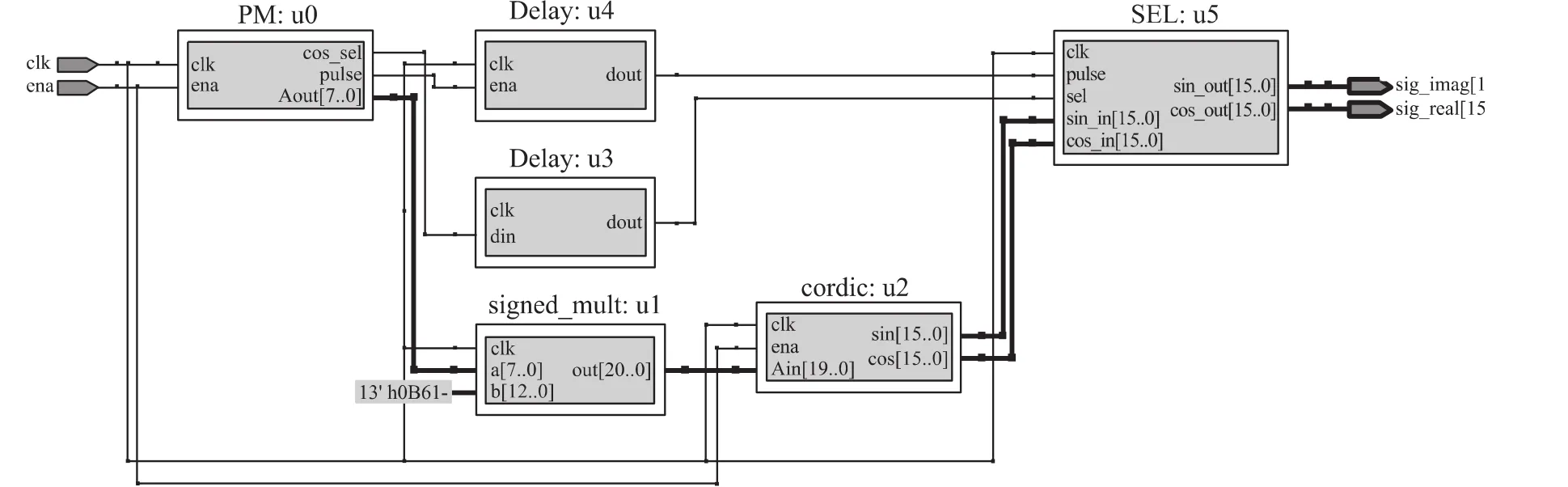
图7 线性调频信号产生的RTL图

在ModelSim中的RTL仿真结果如图8所示，图中上为实部波形，下为虚部波形。

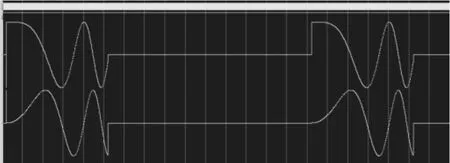
图8 脉冲线性调频信号的波形

4 结论

本文分析了线性调频信号和坐标旋转算法的基本原理，采用Verilog硬件描述语言设计实现了基于坐标旋转算法的 DDS，并产生了线性调频信号。ModelSim仿真结果表明:该方法与传统查表法实现DDS的LFM信号产生方法相比，更节省硬件资源，并具有更高的精度和运算速度。

［1］阮黎婷.非线性调频信号的波形设计与脉冲压缩［D］.西安电子科技大学，2010.

［2］Volder，Jack E.The CORDIC Trigonometric Computing Technique［J］.IRE Transactions Electronic Computers，1959，(8):330-334.

［3］夏少峰，黄世震.基于System Generator的CORDIC算法DDS的FPGA 实现［J］.电子器件，2010，33(1):128-131.

［4］李康.非线性调频信号设计［D］.西安电子科技大学，2009.

［5］刘欣.基于CORDIC的数字下变频电路的ASIC设计与实现［D］.电子科技大学，2007.

［6］夏宇闻.Verilog数字系统设计教程［M］.北京航空航天大学出版社，2008.

［7］Meyer-Baese U.数字信号处理的FPGA实现［M］.清华大学出版社，2011.

［8］赵锦江.基于CORDIC算法的数字调制器设计与实现［D］.国防科技大学，2009.