用于语音降噪的级联滤波器的设计与实现*
包永强
(南京工程学院通信工程学院,南京210096)
目前的一些语音信号识别系统在安静的实验室环境下已达到很高的性能,但在实际的带有噪声的环境下,由于训练模型和识别环境的失配,系统的识别性能往往会有较大幅度的下降。为了提高语音识别系统的抗噪性,研究者提出了很多方法,除了对语音识别模型进行噪声补偿等方法外[1],许多学者致力于研究更具鲁棒性的语音特征。Hwang T H和Lee L M[2]研究了噪声对LPC倒谱系数的影响,并对其进行噪声补偿,提高了其抗噪性。Mansour和Juang[3]提出了短时修正的相干系数 SMC(Short-Time Modified Coherence Coefficient)作为语音特征参数,Javier Hernadot[4]提出了 OSALPC(One-Sided Autocorr-elation Linear Predictive Coding)倒谱系数作为语音特征参数,它们都是基于单边自相关函数序列的线性预测技术,实验证明它们对加性白噪声具有较好的抗噪性。
由于通过单一的变换很难实现语音和噪声完全分离,1999年,Agarwal A[5]等人提出了两级维纳滤波的方法用于克服有色噪声的干扰,获得了很好的效果。两级维纳滤波方法的提出从某种程度上说明了采用两种抗噪算法的系统普遍比只采用一种算法的要好,这种以复杂度换取性能飞跃的算法成为了欧洲电信标准化协会2002年10月颁布的分布式语音识别前端标准中的语音降噪的核心算法[5]。
两级维纳滤波算法的思路说明了存在着这样一种可能——以其寻找一种复杂的变换,达到语音和噪声的最大可能分离,不如将两种普通的降噪算法通过某种方法结合起来,同样可以达到很好的效果。目前国际上正展开对这方面的研究[5-6],因此,寻找这样一种结合方法同时又兼顾其复杂度的算法成为本章讨论的主要内容。
分数阶的概念最早应用于傅里叶变换中,1980年Namias V用Hermite多项式构建了分数傅里叶变换[7-8],第一次给出了分数傅里叶变换的定义,20世纪90年代,Shih C C基于态函数重新给出了一种分数傅里叶变换的新定义[9],Qzatkas H M[10]等人研究发现信号的幂次为α的分数傅里叶变换相当于信号在时频面内角度απ/2的旋转。分数傅里叶变换成为了研究热点,在量子力学、光学、信号处理等领域内得到了广泛的应用。
分数阶理论的引入使得傅里叶变换成为分数阶傅里叶变换的特例,通过改变分数阶值,可使傅里叶变换的内涵得以扩展。由于傅里叶变换在信号处理领域内有着极其广泛的应用,可以预见,分数傅里叶变换具有非常广阔的应用前景[11]。
分数阶变换的提出为两级滤波的研究提供了一个发展方向,可以更加灵活地定义两级维纳滤波中的变换的定义。
本文把ETSI ES 202 050 V.1.1.3版本规定的Mel域上的两级维纳滤波结构推广到分数Mel域上,提出了分数Mel域上的两级维纳滤波结构,获得了性能的提高。
针对语音和噪声在时域和频域重合,而在分数余弦变换域上可能分离的特点,基于分数Mel域上的两级维纳滤波结构,提出了基于态函数的分数余弦变换域上的两级最优滤波器;与Mel域上的两级维纳滤波结构中反复的时域-频域转换带来计算量的急剧上升相比,其计算复杂度得以下降了,并且由于直接在分数余弦变换域上进行滤波,避免了由于Mel域参数较少导致的频域不连续性带来的时域截断噪声。
1 语音处理系统的DSP实现方案
系统由MIC语音输入模块、音频模块和处理模块组成,系统框图如图1所示。语音信号由麦克风输入至TLV320AIC23对语音信号进行AD转换和滤波后,再通过DSP芯片TMS320VC5502对信号进行预处理、特征参数提取、建模及识别构成。
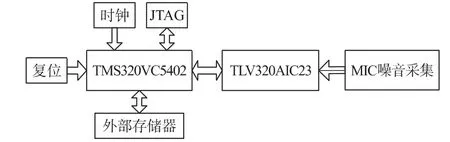
图1 语音系统框图
DSP芯片TMS320VC5502最高可在300 MHz主频下工作,具有16 kbyte的缓存和17 bit×17 bit双乘法器,并带有32 kbit×16 bit的RAM和16 kbit×16 bit的ROM。其片上外设主要包括时钟发生器、DMA控制器、外部存储器接口(EMIF)、主机接口(HPI)、I2C总线、通用输入输出GPIO口、3个多通道缓冲串行端口(McBSP)、两个64 bit通用定时器(GPT)和一个可编程看门狗定时器、通用异步收发器(UART),外部寻址空间达8 Mbyte,可扩展大容量SDRAM。音频编解码芯片TLV320AIC23是可编程芯片,内置耳机输出放大器,内部有11个16 bit寄存器,编程设置这些寄存器可得到所需的采样频率、输入输出增益和传输数据格式等。AIC23通过外围器件对其内部寄存器进行编程配置,其配置接口支持SPI总线和I2C总线接口数据传输格式支持右判断模式、左判断模式、I2S模式和DSP模式,其中DSP模式专门针对TI公司的DSP设计。降噪算法为本文所研究的主要内容。
2 分数余弦变换域上的两级滤波
图2给出了在两次滤波的示意图,图中白色不规则图形的为有用信号,灰色不规则图形为干扰信号,有用信号和干扰信号在时域和离散余弦变换(DCT)域都重叠在一起。无论从时域还是DCT域都无法简单分离有用信号和干扰信号,除非采用复杂的方法。
从图中可以看出,对于时域和DCT域都重叠的有用信号和干扰信号,在分数余弦变换域上,通过简单的两次滤波可以最大程度地消除干扰。
图2说明了这样一个事实,两次简单的变换和滤波能够更有效地消除干扰和噪声。对于噪声环境下的语音信号而言,我们分析它的时域和DCT域的特性,不难发现,语音信号和干扰、噪声无论在时域还是DCT域都是存在着重叠的可能。因此,靠一次降噪处理很难消除干扰和噪声。
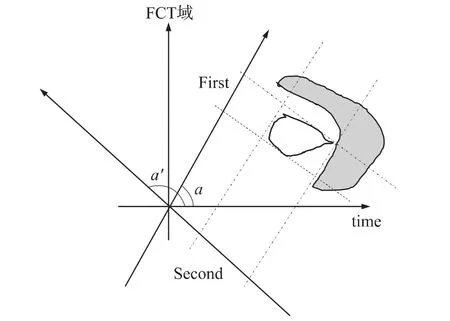
图2 分数余弦变换(FCT)域上的两级滤波示意图
对于含噪语音而言,由于噪声的非平稳性,噪声与语音在时域和DCT域都有可能重叠,如果变换到分数余弦域上,可以最大程度地将其分开。
对于3周期的离散分数余弦变换而言
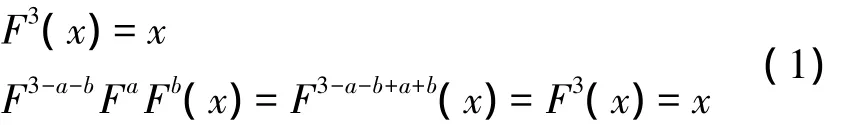
考虑到Mel域上的两级维纳滤波结构,可由两次不同的分数阶余弦变换替换其两次傅立叶变换。具体思路如下:
首先对输入信号进行分数离散余弦变换(FDCT)fa,然后进行滤波Ha(x);对滤波后的信号再进行分数余弦变换fb,再进行滤波Hb(x),然后将输出信号进行分数余弦变换f3-a-b,这样又返回到了时域,取其实部为滤波后的输出语音。
3 分数MEL域上的两级维纳滤波结构
分数Mel域上的两级维纳滤波沿用了ETSI ES 202 050 V.1.1.3版本规定的Mel域上的两级维纳滤波结构。与ETSI ES 202 050 V.1.1.3版本规定的Mel域上的两级维纳滤波不同的是,分数Mel域上的两级维纳滤波的频谱估计的是获取分数幅度谱。不同区域如图2中的灰色部分所示。
在分数余弦变换域上,最佳线性滤波比维纳滤波效果要好。无论是ETSI的Mel域上的两级维纳滤波结构还是分数Mel域上的两级维纳滤波结构,它们的结构都比较复杂,反复的时域-频域转换带来计算量的急剧上升,并且不能够避免由于Mel域参数较少导致的频域不连续性带来的时域截断噪声。
为了进一步降低计算量并提高性能,本节用最佳线性滤波器来代替维纳滤波器;为了避免由于Mel域参数较少导致的频域不连续性带来的时域截断噪声,直接在分数余弦变换域上进行最优线性滤波,该方法称为分数傅立叶域上的两级最佳线性滤波结构TSOFF(Two Stage Optimal Filter Based on FDCT:TSOFF)。
分数余弦变换域上的两级最佳线性滤波流程如图3所示。
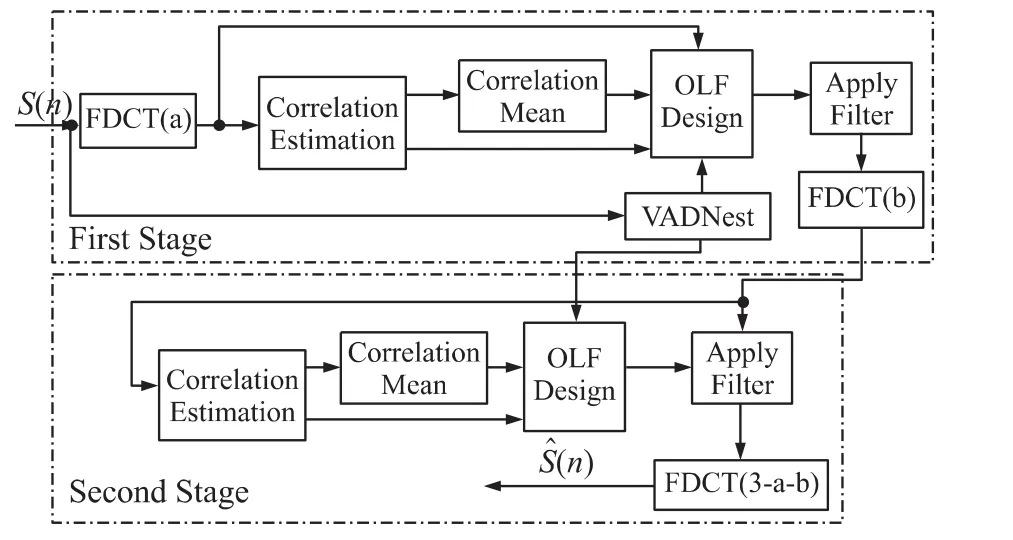
图3 分数余弦变换域的两级最优线性滤波的结构图
与分数Mel域上两级维纳滤波相比,分数余弦变换域上两级最优滤波有以下不同:
(1)采用3周期的离散分数余弦变换代替了分数傅里叶变换;
(2)相关值估计代替了频谱估计;
(3)最优滤波代替了维纳滤波;
(4)滤波直接在分数余弦变换域上进行,省去了一次傅立叶变换,从而使得结构更加简单。
4 噪声环境下分数余弦变换域上滤波器的性能分析
为了分析上提出的分数余弦变换域上TSMWFF、TSOFF滤波器的性能,本节针对不同噪声环境下的语音进行分析。
在本章所有实验中,语音数据为在实验室内录制的语音,采样频率是8 kHz,采样位数8 bit。在纯净语音上叠加高斯白噪声和非平稳噪声(噪声源由英国TNO感知学会所属的荷兰RSRE语音研究中心提供)。
Mel域上的两级维纳滤波在各种实际噪声环境下可以取得良好的性能,本章将其作为基线系统,将本章提出的分数Mel域上的两级维纳滤波与之比较。
表1给出了Mel域两级维纳滤波器(TSMWF)、分数Mel域两级维纳滤波器(TSMWFF)、分数余弦变换域上的两级最佳线性滤波(TSOFF)在高斯白噪声(White Noise)、粉红色噪声(Pink Noise)、Volvo汽车噪声(Volvo Noise)和工厂车间噪声(Factory Noise)下的性能比较。
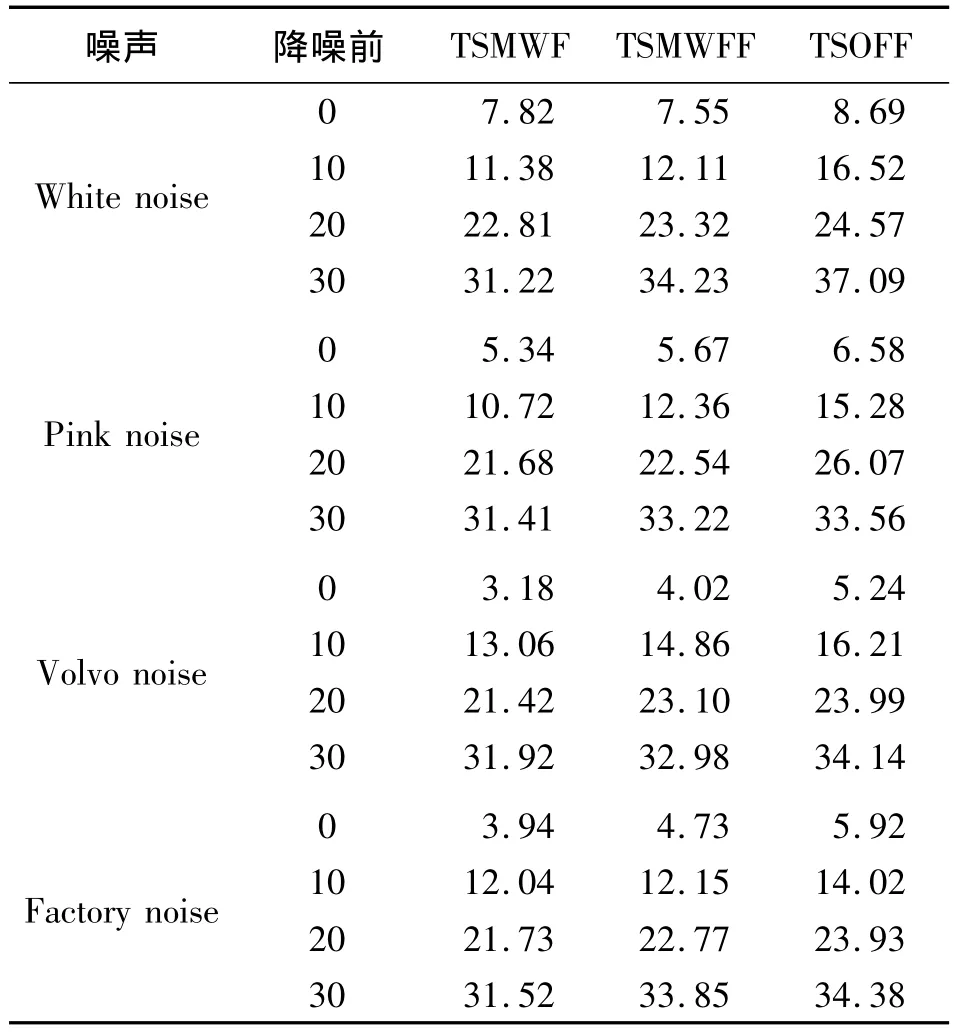
表1 滤波器性能比较 单位:dB
对照表1可以看出,TSOFF法最佳,TSMWFF法其次,TSMWF法最差。与 TSMWF相比,TSMWFF对pink噪声的降噪效果要比其他噪声要更好一些。
5 小结
本文针对语音和噪声在时域和变换域重合,而在分数余弦变换域上可能分离的特点,把ETSI ES 202 050 V.1.1.3版本规定的Mel域上的两级维纳滤波结构推广到分数Mel域上,提出了分数Mel域上的两级维纳滤波结构,获得了性能的提高。
[1]Ivandro Sanches.Noise-Compensated Hidden Markov Models[J].IEEE Trans on Speech and Audio Processing,2000,8(5):533-540.
[2]Hwang T H,Lee L M,Wang H C.Cepstral Behavior Due to Additive Noise and a Compensation Scheme for Noisy Speech Recognition[J].IEE Proc on Vis Image Signal Process,1998,145(5):316-321.
[3]Mansour D,Juang B H.The Short-Time Modified Coherence Representation and Its Application for Noisy Speech Recognition[J].IEEE Trans Acoust,Speech,Signal Processing,1980,28(4):357-366.
[4]Javier Hernando,Climent Nadeu.Linear Prediction of the One-Sided Autocorrelation Sequence for Noisy Speech Recognition[J].IEEE Transactions on Speech and Audio Processing,1997,5(1):80-84.
[5]Agarwal A,Cheng Y M.Two-Stage Mel Warped Wiener Filter for RobustSpeech Recognition[C]//The 1999 International Workshop on Automatic Speech Recognition and Understanding(ASRU’99),December,1999,Keystone,Colorado,USA.
[6]Li Jinyu,Liu Bo,Wang Renhua,et al.A Complexity Reduction of ETSI Advanced Front-End for DSR[C]//Acoustics,Speech,and Signal Processing,2004.Proceedings.(ICASSP '04).IEEE International Conference on Volume 1,17-21 May 2004:I-61-4.
[7]Namias V.The Fractional Order Fourier Transform and Its Application to Quantum Mechanics[J].J Inst Math Applic,1980,25:241-265.
[8]Shih C C.Fractionalization of Fourier Transform[J].Opt Commun,1995,118:495-498.
[9]Pei S C,Tseng C C,Yeh M H,et al.Discrete Fractional Hartley and Fourier Transforms[J].IEEE Trans Circuit SystⅡ,1998,45:665-675.
[10]Pei S C,Yeh M H.Discrete Fractional Hadamard Transform[C]//IEEE Int Symp Circuits Syst,June 1999,1485-1488.
[11]Lohmann A W,Mendlovic D,Zalevsky Z,et al.Some Important FractionalTransformations for SignalProcessing[J].Opt Commun,2003,125:18-20.

