基于CPLD的88键电子琴的设计与实现

付梦婷，付永庆

(哈尔滨工程大学信息与通信工程学院，哈尔滨150001)

电子琴是现代电子技术高度发展并与传统音乐有机结合在一起的一种新乐器。目前市场上有很多种音乐模块，可以直接产生各种曲子，多数集中在使用单片机［1］、555 定时器、逻辑器件组合、LDQ852 集成块、CPLD/FPGA等，这些设计方法各有优缺点，比如使用单片机实现简单、成本低，但是产生的音频过少，很难满足标准电子琴的设计要求及市场需求，而使用CPLD/FPGA器件设计的电子琴虽然实现起来相对复杂，但是设计产生的音频数量能很好地满足标准电子琴的要求，可以说是性价比较高的一类设计［2-4］。随着电子琴设计技术的不断发展，功能更强大，音质更好的电子琴已经成为众多商家竞相追逐的目标。CPLD器件具有静态可重复编程和动态可在系统重构的特性，因其硬件功能可以通过软件编程来修改，故具有很好的设计灵活性和通用性［5］。此外，基于CPLD的电子琴设计还有体积小、系统可靠性高、开发周期短和研制成本低的优点。本文在CPLD器件上开发了一个88键的电子琴音产生电路，通过外部琴键控制其发音，并为CPLD输出的琴音设计了音质提纯电路，使电子琴声音听起来更加真实悦耳。

1 系统设计

基于CPLD的88键电子琴主要由4个模块组成:选择控制模块、电子琴音生成模块、音质提纯模块和电子琴发声模块。前2个模块由CPLD实现，后2个模块由CPLD器件的外部电路实现。选择控制模块支持通过按键选择音频，并对按键抖动进行消除;电子琴音生成模块基于VHDL语言［6］开发产生9个音区共88键电子琴音频;音质提纯模块为带通滤波器电路，用于对CPLD器件输出的方波音频信号进行音质提纯，使电子琴音更加圆润光滑;电子琴发声模块实现电子琴的键音合成与声音输出。

本设计采用的CPLD芯片为ALTERA公司的EPM1270T144I3，实现88键电子琴设计共使用了1079个逻辑单元和97个I/O引脚。本设计的系统原理框图由图1所示，图中BPF为带通滤波器，每个音区采用一个BPF来提纯音质。

图1 电子琴系统原理框图

1.1 选择控制模块的设计

选择控制模块由键盘选择及消抖电路和琴音选通输出部分组成。

1.1.1 键盘选择及按键消抖电路的设计

88键电子琴的键盘使用市场上常见的YAMAHA DGX505电子琴黑白键盘，其中黑键36个，白键52个。88个按键各引出一条控制线与主控芯片相连，用于通过按键对琴音进行控制。

键盘的按键操作中，由于机械触点断开/闭合时会有抖动，信号的传导不会单纯地由1直接跳到0(或由0直接跳到1)，而是会无规律地交替出现0和1的变化，这样只要按一次按键，对主控芯片来说就相当于按了若干次，表现在电子琴演奏上会造成声音的抖动，故须避免。不同类型的按键其最长抖动时间也有差别，抖动持续的时间长短与按键的机械特性有关，一般为5 ms～10 ms。

按键消抖可采用软件的或硬件的方法来解决。常用的硬件消抖电路有计数器型、D触发器型、RS触发器型和状态机型［7-9］。本文采用计数器型消抖电路，假设放开按键产生的键值信号为0，按下为1，计数器数值从0增加到N时代表计时累积达10 ms，则具体消抖过程如下:在每个计数时钟的上升沿到来时，如果按键信号为1，则计数器加1，否则计数器为零，若计数过程中检测到按键信号为0，则计数器清零，判定之前出现的高电平信号为抖动。当计数器数值达到 N时，判定按键按下有效。取CPLD主时钟频率为100 MHz，若直接对其计数，则达到10 ms需计数1 000 000次，故会占去大量逻辑单元，而88个键都要消抖，所需逻辑单元数会远超1 270个。为节省逻辑单元，本设计取小字二组频率为698.456Hz的#f2音作为计数时钟，因此只需计数7次便可达到10 ms计时。

因计时达10 ms后直至按键松开一直都要输出该键对应的音频信号，故需另外定义一个在该时间范围内为高电平，而其余时间均为低电平的按键输出选通信号。记计数变量为Count，按键输出选通信号为Key，则以VHDL语言设计的消抖电路工作流程如图2所示。

图2 消抖电路的工作流程图

1.1.2琴音选通输出部分的设计

在选择输出部分，当电子琴键盘的按键被按下时，主控芯片从88个基本琴音中选择相应的音频输出。根据电子琴弹奏原理，电子琴的琴音存在和弦现象，即当电子琴的不同琴键同时被按下时，产生的琴音应由所按键盘选出的琴音合成产生。琴音的合成即信号的相加，数字信号的相加可通过异、或运算实现，而模拟信号的相加可通过模拟加法器实现。为实现这一功能，设计中同一音区琴音的和弦通过软件中数字信号的异、或运算实现，不同音区琴音的和弦通过硬件电路中带通滤波器后的加法器实现。

1.2 电子琴音生成模块的设计

对电子琴音生成模块的设计即对分频器的设计，利用分频器对100 MHz的晶振时钟分频可依次得到所需的88个琴音。

音乐的十二均率规定:每两个相邻八度音之间的频率相差一倍;在两个相邻八度音之间，又可分为十二个半音。这里设计9个音区共88个音的音频，频率范围从27.5 Hz～4 186 Hz，这九个音区分别是大字二组、大字一组、大字组、小字组、小字一组、小字二组、小字三组、小字四组、小字五组，其中大字二组只包含A2、#A2和B2 3个音，小字五组只有c5一个音，其余音区各含12个音。88键电子琴的小字一组的音符与琴音频率的对应关系如表1所示。

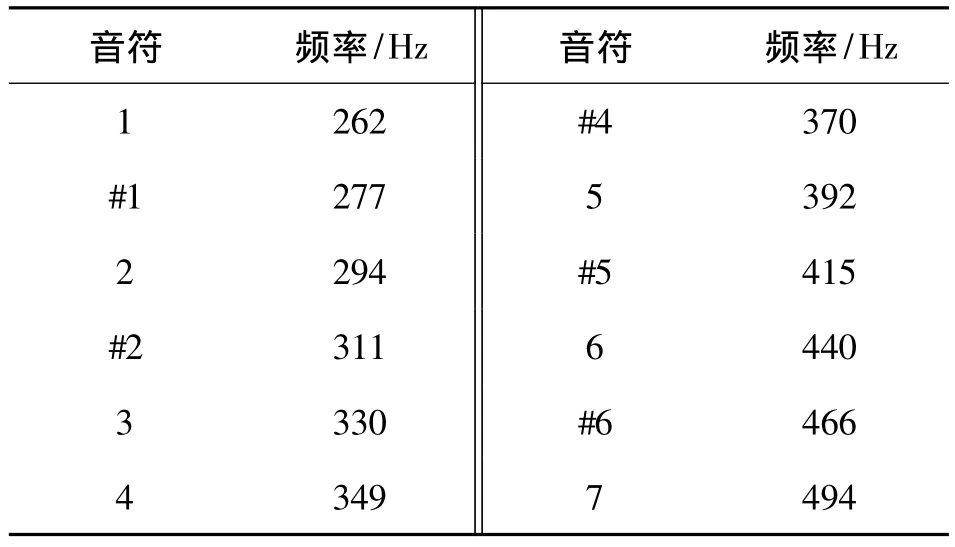
表1 小字一组电子琴琴音频率对照表

表中，带#号的音符表示半音，其他的音符为全音。这里用Ck(k=1，2，…，12)表示小字一组的12个琴音频率，即C1=262 Hz，C12=494 Hz。因每两个相邻音区之间的频率相差一倍，故若对比小字一组频率高几倍音区的琴音频率用在Ck上方加几点的方式表示，对比小字一组频率低几倍音区的琴音频率用在Ck下方加几点的方式表示，则可给出以小字一组琴音频率表达的各音区的琴音频率为:

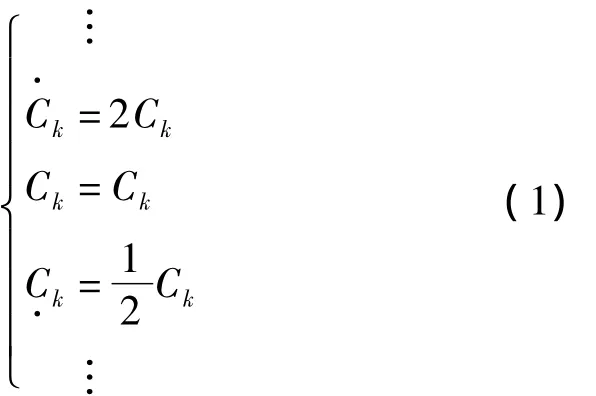
由式(1)知，琴音生成时只须先产生最高音区的12个琴音频率信号，然后采用逐次二分频的方法可获得所有音区的琴音频率信号。这样做既能降低设计工作量也能减少对CPLD芯片逻辑单元的需求量，因此可取得节约硬件设计成本的目的。

通过分频获得小字一组琴音频率(分频器)的设计原理是:将系统主时钟作为加法计数器的计数时钟，每当主时钟的上升沿到来时，让加法计数器计数一次，当计数累积结果达到N时，计数器复位且使输出取反，如此反复就能得到所要的琴音频率。由于通过两次取反方能得到输出信号的一个完整周期，故N的数值应等于系统主时钟频率与所要输出琴音频率比值的一半。以产生4 186 Hz的琴音频率为例，N值应为100 MHz/4 186 Hz/2=11 994。

1.3 音质提纯电路设计

由于分频器输出的琴音信号为方波，含高次谐波成分较多，故音质不纯，所以，需要把它转换成音质柔和且纯正的正弦波琴音信号。按照傅立叶分析，任何周期信号都可以用一组三角函数的组合表示。

不失一般性，假设方波琴音信号的时域表达式为:

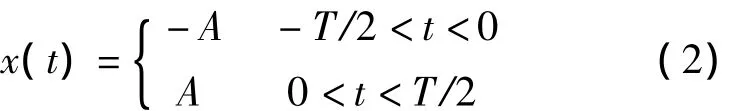
则由傅立叶变换可得其三角函数展开式为:

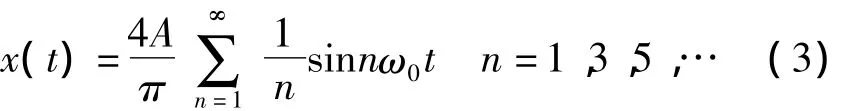
可见，周期方波是由一组频率成分成谐波关系、幅值成一定比例，相位角为零的正弦波叠加合成的。因此只需要将方波信号的高次谐波滤除，剩下基波信号输出，就能达到将方波转换为正弦波的目的。

为提纯琴音信号，采用美国Burr-Brown公司的通用型集成有源滤波器UAF42设计成带通滤波器来完成该项任务。该芯片在使用时，只要根据设计公式计算合适的外接电阻，再经简单连接就能很好地满足设计要求［10］。UAF42芯片工作频率在10 Hz～100 kHz范围内时不需要外接匹配电容，因电子琴的88个琴音频率均在此范围内，故UAF42的同相输出二阶带通滤波器设计公式为:

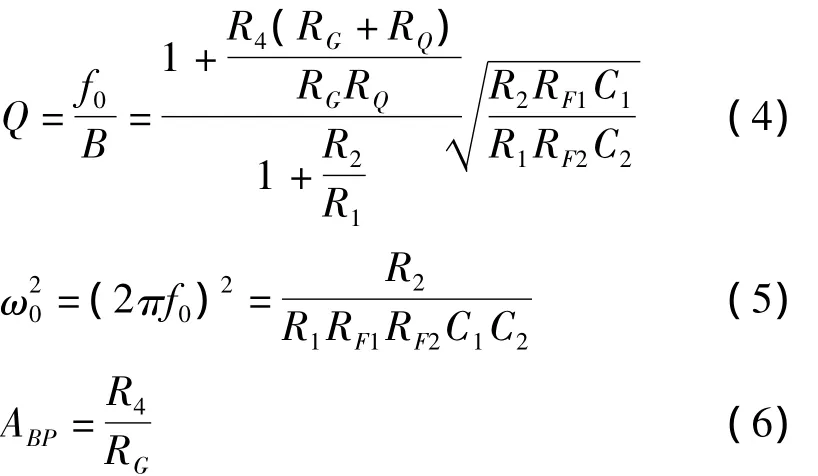
由UAF42内部电路知，若取R1=R2=R4=R=50 kΩ，C1=C2=C=1 000 pF，则只需根据滤波器的中心频率、带宽及所需放大倍数即可算出四个电阻RF1、RF2、RG和RQ。为方便计算，取RF1=RF2，则式(4)可化简为:

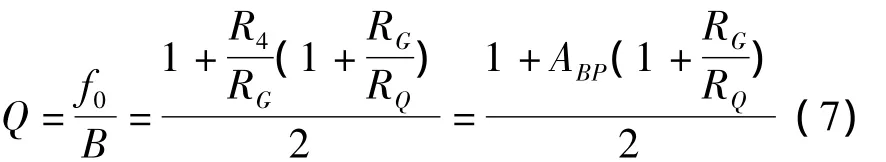
取放大倍数ABP=1，则由式(5)～式(7)得:

式(8)为带通滤波器设计的基本计算公式，只需提供带通滤波器的中心频率及带宽即可计算出相应的带通滤波器的外接电阻值。

设计时，若对每个音频输出都设计一个滤波器，输出的声音信号固然很好，但需设计88个带通滤波器，显然电路将过分复杂且成本也过高。但若只设计一个滤波器，则因带宽相对于中心频率来说太大，滤波效果也会不够理想。为减少电路复杂性和成本又不使滤波效果受到明显影响，可把每个音区的12个琴音频率划分为一组用一个带通滤波器滤波。因相邻音区的琴音频率相差一倍，故每组琴音中最小频率琴音的二次谐波频率大于最大频率琴音的频率，因此理论上经带通滤波器后可滤除组内所有琴音频率的谐波分量，只剩下基波分量，从而使音色纯净。由于小字五组只有c5一个音，分组时将其归到小字四组，则88个琴音共分为8组，将最高音区组记为第8组，其含有13个琴音，而第2组～第7组均含有12个琴音，第1组含有3个琴音，因此需要设计8个带通滤波器来实现音质提纯。

经测试发现经带通滤波器输出的正弦波仍有一定程度的失真，其频谱主要为二、三次谐波分量，故在带通滤波输出后加入了一阶低通滤波器做进一步的滤波处理以提高琴音音质质量。

1.4 电子琴发声模块

在完成了对音频信号的提纯设计后，需将各路音频信号合并，使其合成为一路信号作为最终的输出信号，并送给扬声器发出声音。这里基于LM324设计了一个同相加法器［11］，如图3所示。

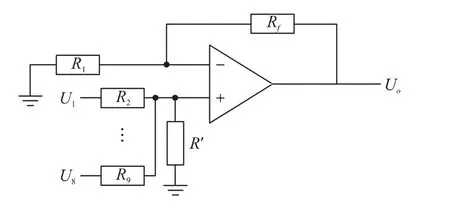
图3 同相加法器电路

图中，U1～U8是滤波器输出的8路提纯信号，Uo是最终的合成信号，满足:

取R1=R2=R3=…=R9=R'=R，则:

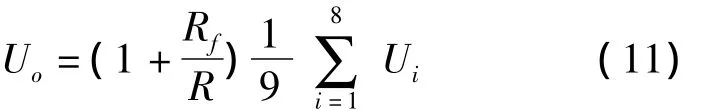
由式(11)知，它给出的不只是一个加法器，同时也是一个电压放大器。考虑到多键按下时的和弦情况，8路信号加起来可能会出现高电平同时叠加，导致输出电压被限幅，产生信号失真，因此反馈电阻Rf阻值不宜过大。设计时取R=10 kΩ，Rf采用10 kΩ的滑动变阻器。由于8路带通滤波器的放大倍数均为1，则U1～U8的幅度相同，若设为U，则8路同时有信号输入时，Uo可输出的电压幅度范围为，少于8路信号时则输出的电压的幅度变化范围更小些。经测试，1倍放大的单路滤波器输出信号经过加法器电路后不会出现波形失真，则调节Rf的值使Uo输出的电压幅度为U或更小即可避免超出限幅电压的情况，同时要保证输出电压也不能过小，以保证扬声器正常发声，因此试验时需要反复调节，边观看示波器上的输出波形有无限幅失真同时监听扬声器的输出音量，以达到最佳平衡状态为宜。

2 功能验证

验证本文的设计有两种途径，进行 QuartusⅡ［12］环境下的波形仿真和由示波器观测电子琴系统的实际输出波形。

2.1 琴音生成功能验证

以小字三组的最高音频b3为例，该琴音的实际频率为1 975.53 Hz。将CPLD对该琴音的输出接示波器，得到的波形图、频率值及频谱特性如图4所示。

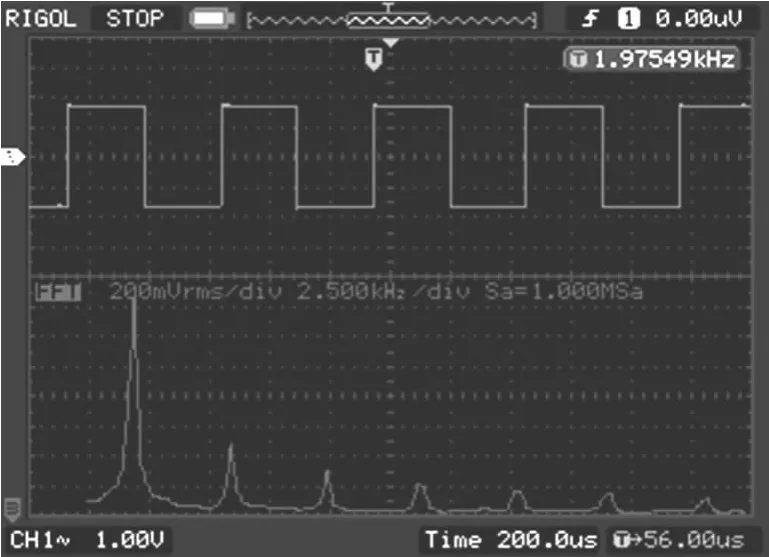
图4 分频生成的小字三组的最高音频b3特性

由图可见，输出波形为方波，频率约为1 975.49 Hz，与设计要求基本一致。频率上的微小差异，除与分频器N值四舍五入取法有关外，与示波器测频精度也有一定关系，因频率误差很小故对琴音的听觉感受基本无影响，即电子琴的音准性能达到了设计要求。

2.2 消抖功能验证

由2.1.1节可知，以#f2琴音作为计数时钟，计数7次可消除持续时间小于10 ms的抖动。假设计数变量为Count，则其取值范围为0～6，仿真结果如图5所示。

图中，key_in为高电平有效的按键信号，key_xiaodou为去抖后的按键输出选通信号，key_signal为与之对应的音频信号，music为按键选出的琴音信号。

图5 琴键消抖波形图

由图可见，所设计的消抖电路消除了按键按下和松开时的抖动。另外，key_in下降沿到来时，music信号没有立刻输出低电平，而是延迟了一段时间才输出低电平，这由消抖电路本身存在的延时所引起。

2.3 同一音区多键按下时和弦功能验证

2.3.1 从波形仿真上验证

为便于仿真，设音区中含有三个按键，按键信号分别为key_in1、key_in2和key_in3，对应的方波音频信号分别为key_signal1、key_signal2和key_signal3。设与key_in1和key_in2相应的按键同时按下，music为输出信号，按键信号高电平有效，则在QuartusⅡ［12］环境下仿真得到的波形如图6所示。

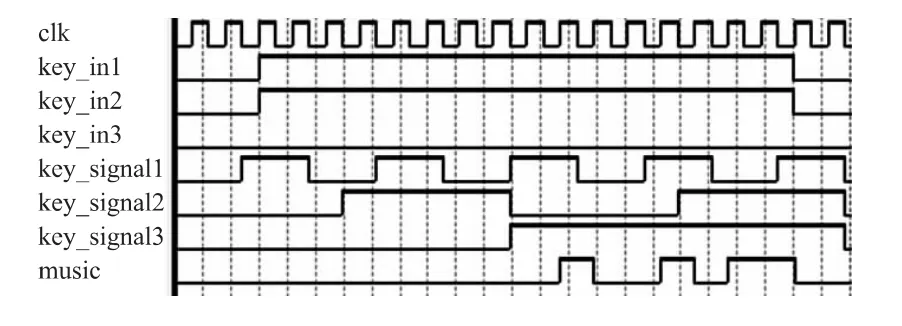
图6 同一音区两键按下时和弦波形图

由图6可见，music为key_signal1与key_signal2的异或，实现了同一音区多键按下时输出和弦音信号的功能。此处仍考虑了消抖，因此输出相对于按键按下有一定的延时。

2.3.2 从系统输出波形上验证

以小字三组为例，该组琴音频率范围是1046.5Hz～1975.53 Hz，选取与其中的7个全音对应的按键同时按下。由于示波器给出的频谱结果精确不够，故利用示波器的数据存储功能，先导出这7个音和弦的时域波形数据，再用MATLAB做频谱分析，得到的结果如图7所示。

由图7可见，在滤波器的频带内含有7根较高的谱线，即7个琴音都通过了音区带通滤波器，因此实现了和弦的功能。不过带外仍有少量谐波频谱存在，这是由7个琴音之间形成的组合频率干扰，加之滤波器无法达到理想带通滤波性能所致，但其干扰程度已受到一定的抑制。

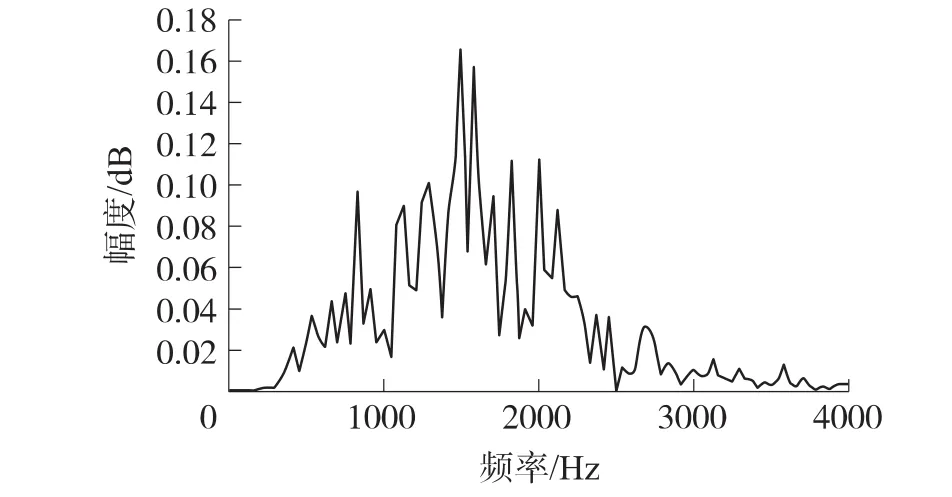
图7 同一音区两键按下时和弦波形及频谱图

2.4 滤波器的音质提纯功能验证

2.4.1 带通滤波器的幅频特性测试

对带通滤波器幅频特性的测试采用信号发生器和示波器进行。以小字三组对应的第7组滤波器为例，滤波器的滤波范围是1 046.5 Hz～1 975.53 Hz，中心频率约为1 502 Hz，带宽约为929 Hz。由信号发生器输出一个幅度为500 mV，频率可变的正弦信号，将信号送入滤波器，用示波器观测其输出。边调节正弦信号的频率，边观察与记录不同频率输入信号所对应的输出信号的幅度，并以此数据用MATLAB画出其幅频特性曲线如图8所示。

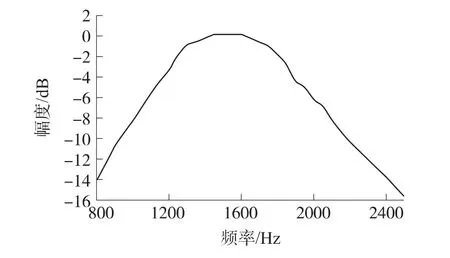
图8 第7组带通滤波器幅频特性图

由图8可以看出，滤波器中心频率约为1 500 Hz，且将频率在1 500 Hz左右的信号放大了1倍，1 000 Hz以下及2 000 Hz以上频率的信号衰减较大，起到了滤除带外谐波的作用。

2.4.2 音质提纯电路的滤波效果测试

采用示波器分别测CPLD输出的音频波形和该音频信号经过滤波器后的输出信号，仍以小字三组的最高音频b3为例，该琴音的实际频率为1 975.53Hz，测试结果如图9所示。其中，图(a)为滤波前的方波信号及滤波后的正弦波信号，从时域波形图上看，滤波前后频率一致，且正弦波较理想，滤波效果较好。图(b)对所得到的正弦波进行了频谱分析，可见二、三次谐波分量相比基波分量已极其微弱，更高次的谐波分量已经基本上不存在了，显然，频域数据也证明了滤波器的滤波效果。

另外，将不通过滤波器发出的声音与通过滤波器后发出的声音进行比较，能明显听出音质的差异。不接滤波器时声音比较尖锐刺耳，而接上滤波器后，声音变得圆润悦耳。这就从实践上证明了滤波器设计的有效性。

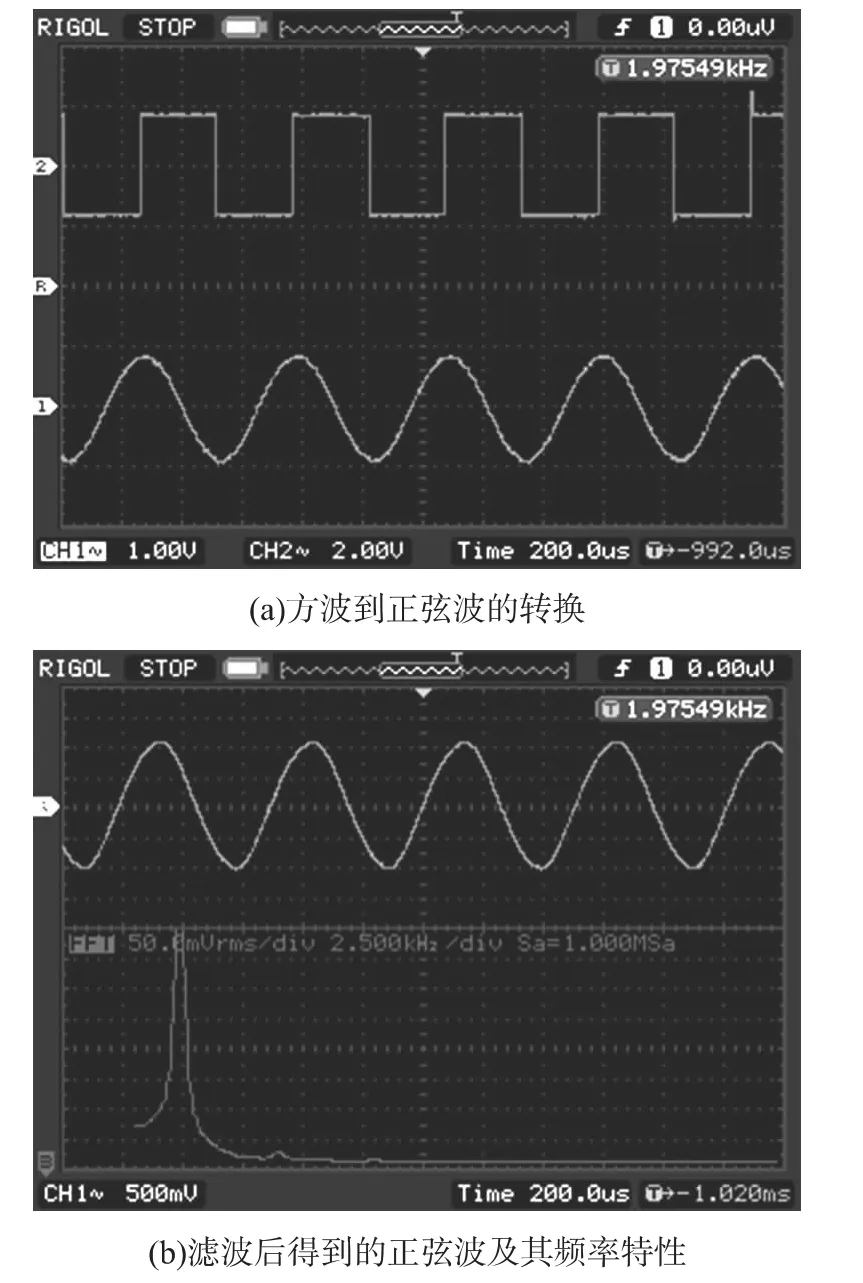
图9 滤波器滤波效果图

3 结束语

本系统采用Altera公司的CPLD芯片EPM1270T144在QuartusⅡ平台上设计了88键电子琴，将电子琴的核心部分集成在了CPLD芯片上，简化了外围电路，设计成本较低。理论仿真及实验测试结果均表明，计数器型消抖电路能很好地消除键盘抖动，设计的琴音音色提纯滤波器起到了使琴音圆润悦耳的目的，同时本设计也实现了电子琴的和弦功能。综上可见，本文设计的电子琴很好地实现了预期设计目标，可为基于CPLD芯片设计电子琴提供有益的理论参考和实践指导。

［1］任肖丽，王骥.基于STC89C51单片机的电子琴设计［J］.电子元器件应用，2010，12(7):27-31.

［2］安雪娥，潘汉怀.基于CPLD的电子琴系统设计［J］.信息与电脑，2009，21(11):25.

［3］姬晔.基于 FPGA的音乐合成器设计［D］.吉林:吉林大学，2010

［4］张卿.基于FPGA的音乐演奏电路及电子琴的设计［J］.现代经济信息，2009(16):285-287

［5］刘延飞.基于Altera FPGA/CPLD的电子系统设计及工程实践［M］.北京:人民邮电出版社，2009:1-17.

［6］付永庆.VHDL语言及其应用［M］.北京:高等教育出版社，2005:55-56，133-138，171-173.

［7］张友木.基于VHDL语言的几种消抖电路的设计［J］.山西电子技术，2011(1):1674-4578

［8］候继红.基于VHDL语言的按键消抖电路设计及仿真［J］.现代电子技术，2009(23):201-202

［9］许德成.基于FPGA的按键消抖动设计［J］.吉林师范大学学报(自然科学版)，2009(4):154-156

［10］杨振江，余进.多用途有源滤波器UAF42的应用［J］.电子技术应用，1997，7(9):47-49

［11］谢红.模拟电子技术基础［M］.哈尔滨:哈尔滨工程大学出版社，2002:226-228.

［12］徐刚.Altera QuartusⅡ软件使用教程［Z］.芳园电子工作室，2006.