卫星490N发动机安装位置优化研究
胡伟 金煌煌 王庆华
(北京空间飞行器总体设计部,北京 100094)
1 引言
490N 轨道控制发动机是中国于20世纪90年代初研发的用于地球同步轨道卫星远地点变轨的发动机,也是现有各种高轨道卫星平台通用的主推发动机[1-3]。由于其自身结构及地面调校不完全精准,490N 发动机会产生偏离主推力方向的斜向推力,通过地面试验可以标定出发动机推力矢量在发动机坐标系中的位置。当发动机安装到卫星上后,根据其安装位置可获得发动机坐标系和卫星坐标系之间的转换关系,从而确定发动机推力矢量在卫星坐标系中的位置。
如果490N 发动机推力矢量通过卫星质心,则推力不会对卫星姿态形成干扰力矩;但由于发动机推力矢量自身的偏斜,加之在变轨过程中卫星质心位置不断变化,致使发动机推力矢量不能始终通过卫星质心,从而对卫星的姿态产生干扰[4-5],引起额外的推进剂消耗;当干扰力矩过大时,甚至会导致卫星姿态失控,造成严重的后果。为尽量减小变轨过程中的这一干扰力矩,满足姿态控制要求,减少推进剂消耗,应综合考虑卫星质心位置变化的范围,通过调整发动机安装位置,使其推力矢量指向优化的方向,确保干扰力矩满足使用要求。
本文首先描述了490N 发动机的推力矢量及其对卫星产生的干扰力矩的计算过程;然后提出了一种优化方法,即在满足工程装配约束条件下,根据卫星质心位置变动范围选取推力指向,并通过调整发动机安装位置来减小干扰力矩;结合实际工程中发动机安装实施的过程,对比了优化安装位置前后干扰力矩的变化情况,并进行了分析,可为工程中确定卫星变轨发动机安装位置及实施安装提供参考。
2 坐标系定义及推力矢量描述
2.1 坐标系定义
在计算发动机推力产生的干扰力矩时,涉及到发动机坐标系和卫星坐标系,如图1所示。发动机坐标系是以发动机安装平面的几何中心为原点O,以安装平面为YOZ平面,并以安装平面的垂线为X轴,形成与发动机固连的直角坐标系。发动机推力矢量F的作用点P和指向是在发动机坐标系中定义的。卫星坐标系以星箭分离平面的几何中心为原点O′,以星箭分离平面为Y′O′Z′平面,并以星箭分离平面的垂线为X′轴,形成与卫星固连的直角坐标系。卫星质心C的位置是在卫星坐标系中定义的。
当发动机对接到卫星后,发动机坐标系的X轴与卫星坐标系的X′轴重合,发动机坐标系的Y轴和Z轴分别与卫星坐标系的Y′和Z′轴平行,即发动机坐标系原点O相对于卫星坐标系原点O′只存在X轴方向的一段平移,平移距离称为发动机的安装距离d。安装发动机时,通常要在此对接位置的基础上进行调整,优化两个坐标系之间的相对位置,以减小推力对卫星质心的干扰力矩。
2.2 发动机推力矢量的测量
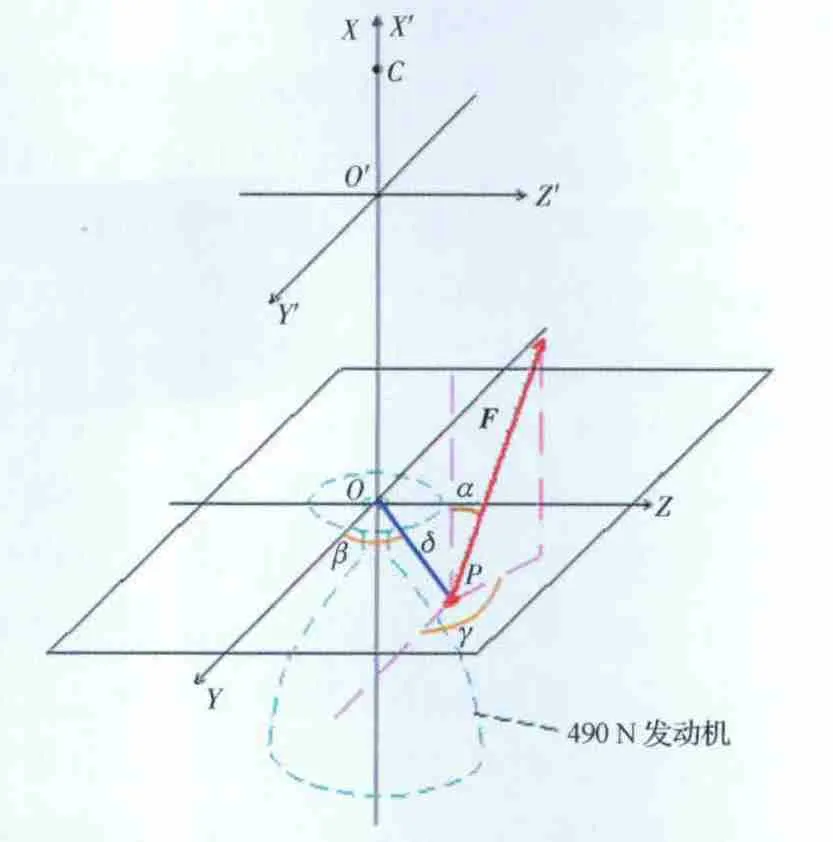
图1 发动机坐标系与卫星坐标系示意Fig.1 Thruster coordinates and satellite coordinates sketch
由于制造和个体的差异性,每台490N 发动机都具有不同的推力矢量,且都会进行地面热试车试验,并将相关试验数据作为发动机性能参数。其中,一部分参数用于描述发动机推力矢量F在发动机坐标系中的大小、方向和作用点(见图1),其中,真空推力|F|用于描述推力矢量的大小;推力偏斜角α用于描述推力矢量与发动机坐标系X轴的夹角;横移距离δ用于描述推力作用点P到发动机坐标系原点O之间的距离;横移位置角β用于描述推力作用点P在发动机坐标系YOZ平面内的位置角;偏斜位置角γ用于描述推力矢量的方位角,即推力矢量在发动机坐标系YOZ平面内投影与Y轴的夹角。
在理想情况下,发动机的推力只作用在主推方向(X轴方向),即推力作用点与发动机坐标系原点重合,发动机推力矢量F与坐标系X轴重合;但实际上,由于生产调校不完全精确,推力矢量会存在偏差,通过上述标定参数可确定每台发动机实际的推力矢量。
3 减小干扰力矩的优化方法
3.1 推力方向的优化目标确定
设L为质心C指向推力作用点P的矢量,则发动机推力对卫星质心的干扰力矩M[6]可由式(1)计算,干扰力矩M的模可由式(2)计算。
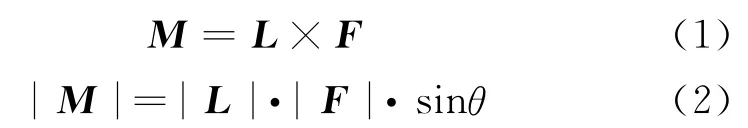
式中:θ为矢量L与推力矢量F之间的夹角。
当发动机对接到卫星进行安装位置调整时,由于装配接口的限制,发动机坐标系沿卫星坐标系X′轴的平移和旋转都受到限制,因此发动机安装距离d和横移位置角β的可调整范围很小,|L|的大小在安装位置调整过程中基本保持不变,而推力大小|F|也是固定的,所以要减小干扰力矩的大小|M|,只能通过减小矢量L与推力矢量F之间的夹角θ来实现。在卫星变轨过程中,质心C的位置在不断变化,通常,在对卫星质量进行特性分析时,会给出卫星每次变轨开始和停止时的质心位置Cib和Cie(i=1,2,3,…n,表示第几次变轨,n表示变轨总数)。本文根据质心位置变化的范围,选取变轨过程中各阶段质心位置Cib和Cie的中心Cc(即质心位置坐标的平均值)作为推力矢量F的目标指向,以达到在变轨全过程中减小θ的目的。
3.2 发动机安装位置的调整与测量
发动机安装位置调整过程是将推力矢量F调整到指向质心变化范围中心Cc的过程。由于受到装配约束,调整只能由在YOZ平面内的小范围平动和绕Y、Z轴的小范围旋转组成,在此约束条件下,可使推力矢量F绕其作用点P作定点旋转指向中心Cc来实现。在发动机安装的工程实施过程中,此调整是通过精测镜测量发动机坐标系原点O在卫星坐标系中的位置,以及发动机坐标系-X轴在卫星坐标系中的方向角来确定的[7]。为了便于在卫星坐标系中使用矩阵表示调整的过程,并计算出调整后上述工程测量的目标值,可将调整分解为以下3步。
(1)平移发动机坐标系,使推力作用点P与卫星坐标系原点O′重合;
(2)以卫星坐标系原点O′为中心旋转发动机坐标系,使推力矢量F指向转到原推力作用点P与卫星质心Cc的连线方向;
(3)平移发动机坐标系,使推力作用点P回到最初在卫星坐标系中的位置。
在卫星坐标系下,每一步调整均可用坐标变换矩阵来表示(为了用矩阵表示平移,可用计算机图形学中归一化的坐标变换方式增加一个坐标维度,因此坐标变换矩阵是4×4方阵[8]),分别将3步调整的坐标变换矩阵记为T1,T2,T3,则安装位置优化调整的坐标变换矩阵为T=T3T2T1。由坐标变换矩阵T可计算出发动机安装位置调整后,在卫星坐标系中发动机坐标系原点O的位置坐标及-X轴的方向角,作为工程中发动机安装调整的要求。
4 发动机安装调整实例
以某卫星490N 发动机的安装为例,其地面热试车试验数据如下:真空推力|F|为489.18N,推力偏斜角α为0.18°,横移距离δ为0.36mm,横移位置角β为123°,偏斜位置角γ为109°。发动机的安装距离d为84.60 mm;卫星在3 次变轨过程中质心位置坐标(单位:mm)分别为(1 056.90,0.00,0.00)T,(1 033.50,0.00,0.00)T,(1 033.90,0.00,0.00)T。
根据发动机与卫星对接后发动机坐标系与卫星坐标系之间的位置关系,以及发动机的地面热试车试验数据,可计算出在优化安装位置前卫星坐标系中,推力作用点P的坐标(单位:mm)为(-84.60,-0.20,0.30)T,推力矢量F的坐标(单位:N)为(489.177,-0.500,1.453)T,对应3次变轨质心位置的干扰力矩坐标(单位:N·m)分别为(-0.000,1.806,0.667)T,(- 0.000,1.772,0.655)T,(-0.000,1.773,0.656)T。质心变化范围中心Cc的坐标(单位:mm)为(1 041.40,0.00,0.00)T。
按照上述发动机安装位置优化方法,3 步调整的坐标变换矩阵分别为

由坐标变换矩阵T,可计算出调整后在卫星坐标系中推力作用点P的坐标(单位:mm)为(-84.60,-0.20,0.30)T,调整后推力矢量F的坐标(单位:N)为(489.179,0.085,-0.131)T。安装位置优化后对应3次变轨质心位置的干扰力矩坐标(单位:N·m)分别为(0.000,-0.002,-0.001)T,(0.000,0.001,0.001)T,(0.000,0.001,0.001)T。表1中对比了发动机安装位置优化前后的3次变轨质心位置所对应干扰力矩,可见,调整安装位置后,干扰力矩显著减小。

表1 优化前后的干扰力矩对比Table 1 Comparison of interference torque before and after optimization
由坐标变换矩阵T,也可以计算出安装位置优化后发动机坐标系原点O在卫星坐标系的位置坐标(单位:mm)为(-84.60,0.10,-0.27)T,发动机坐标系-X轴在卫星坐标系中的方向角分别为179.802°、90.069°和89.814°,可作为490N 发动机安装的工程实施要求。
5 结束语
490N 发动机推力对卫星形成的干扰力矩,与发动机安装位置和卫星质心位置密切相关。本文提出的发动机位置优化方法,综合考虑了发动机地面热试车试验数据和卫星质心位置变化等影响因素,不仅适用于490N 发动机安装位置的调整,也可用于其他变轨发动机安装位置的优化,以减小干扰力矩。不过,该方法是基于方便工程安装实施的目标提出的,其中确定推力最优指向的方法也较简单,所确定的发动机安装位置并不是使卫星变轨全过程中干扰力矩最小的最优位置。最优安装位置要结合卫星质心位置变化的空间分布进行复杂解算,并且还要进一步研究如何保证其工程实施的可行性。
(References)
[1]陈健,曹永,潘海林,等.双模式化学推进技术发展研究[J].火箭推进,2006,32(4):31-37
Chen Jian,Cao Yong,Pan Hailin,et al.The development of dual-mode chemical propulsion systems[J].Journal of Rocket Propulsion,2006,32(4):31-37 (in Chinese)
[2]姜文龙,杨成虎,林庆国.高性能卫星用490N 轨控发动机研究进展[J].火箭推进,2011,37(6):9-13
Jiang Wenlong,Yang Chenghu,Lin Qingguo.Development of high performance 490Napogee engine for satellites[J].Journal of Rocket Propulsion,2011,37(6):9-13(in Chinese)
[3]Liu Changguo,Chen Jie,Han Hongyin,et al.A long duration and high reliability liquid apogee engine for satellites[J].Acta Astronautica,2004,55(3):401-408
[4]王寨,李铁寿,王大轶.探月卫星变轨时的姿态控制研究[J].航天控制,2005,23(1):11-14
Wang Zhai,Li Tieshou,Wang Dayi.Attitude control during lunar satellite orbit maneuver[J].Aerospace Control,2005,23(1):11-14(in Chinese)
[5]向东,杨庆俊,包钢,等.三轴气浮平台常值干扰力矩的分析与补偿[J].宇航学报,2009,30(2):448-452
Xiang Dong,Yang Qingjun,Bao Gang,et al.Research on analysing and compensation of the steady disturbing torque of the three axis air bearing table[J].Journal of Astronautics,2009,30(2):448-452(in Chinese)
[6]屠善澄.卫星姿态动力学与控制[M].北京:中国宇航出版社,2001
Tu Shancheng.Satellite attitude dynamics and control[M].Beijing:China Astronautics Press,2001(in Chinese)
[7]马海全,李竞蔚.复合材料桁架式发动机支架改型设计分析[J].强度与环境,2006,33(4):39-43
Ma Haiquan,Li Jingwei.Retrofit design and analysis of composite truss structure of orbit maneuver motor bracket[J].Structure & Environment Engineering,2006,33(4):39-43(in Chinese)
[8]Rogers D F.Procedural elements for computer graphics[M].New York:The McGraw-Hill Companies,1998

