一种在轨卫星质量特性计算方法
张洪波 武向军 刘天雄 丛飞 周耀华
(北京空间飞行器总体设计部,北京 100094)
1 引言
卫星需要通过高精度轨道和姿态控制,来实现星体及有效载荷的高精度指向,以完成复杂的空间任务。为了实现卫星姿态高精度控制,需要已知星体准确的质量特性参数(包括质心、转动惯量和惯性积)。在国内外实际航天工程应用中,卫星质量特性参数多源于地面测量,但地面质量特性测量虽耗费大量人力、财力和研制周期,却无法实现高精度、全生命周期和状态的测量[1],这是由于:第一,重力和测试装置本身的影响无法完全消除;第二,太阳翼、天线等部件展开状态质量特性无法测量;第三,卫星惯性积量级较小,与一些系统测量误差量级相当,导致惯性积测量结果不可用。为此,可借助星上敏感器和执行机构计算卫星在轨质量特性,这样不仅可以实时反映质量特性在轨变化情况,控制系统可自动适应变化来实现卫星高效、高精度的姿态控制,而且计算分析结果对于卫星总体构型布局优化、卫星表面展开部件设计优化、地面测量系统误差修正也具有指导意义。
截至目前,国外已有一些学者开展了卫星在轨质量特性计算方法研究。Bergmann等人提出了一种基于高斯二阶滤波的计算方法[2-3],此算法逻辑复杂、计算量大,并对动力学模型进行了简化,只适用于卫星转动角速度足够小的情况;Wilson和Rock等人提出了一种基于指数加权递归的最小二乘法[4-5],此算法需要卫星配置线加速度计,且计算过程中通过动力学方程的线性近似,人为割裂了质量、惯量和质心的内部耦合关系,虽然采用“递归”方法可以逐步减小或忽略耦合引起的误差,但在卫星角速度较大的情况下误差也较大;Tanygin 和Williams等人提出了一种使用最小二乘法在自旋卫星执行在轨机动时辨识其质量特性的方法[6],不适用于三轴稳定卫星;Kim 等人提出利用递归最小二乘法辨识三轴航天器的惯量和质心位置[7-8],存在与Wilson等人算法类似的问题。国内在该方面的研究还不多[9],王书廷等人提出了一种基于递归最小二乘法的卫星惯量和质心位置计算方法[10],思路和问题与文献[5]类似;徐文福等人提出了基于POS优化的计算方法[9]。对于国内外的上述计算方法,有以下4点因素限制了其精度和应用范围:①需要卫星配置线加速度计;②割裂参数内部耦合关系,需要假设卫星旋转足够慢;③未考虑星体与飞轮的动量交换,并假设星体采用零动量控制方式来简化耦合关系;④一些不进行在轨姿态大角度机动(连续转动,且绕三轴均有角速度和角加速度分量)的卫星,不适用递归算法。
基于上述问题,本文提出一种基于批量最小二乘法的质量特性计算方法,仅需要卫星配置陀螺,针对偏置动量控制方式建模并考虑星体与飞轮动量交换,通过交互迭代的方式逐步消除耦合误差,计算基于若干离散喷气运动状态,不需卫星连续喷气转动。此方法对于卫星配置和运动状态要求低,充分考虑了参数耦合关系,适用范围更广。
2 在轨卫星姿态动力学建模
2.1 坐标系定义
卫星坐标系定义[11]如下:
(1)星体坐标系ObXbYbZb:原点Ob位于星箭分离面中心,对地模式下ObXb轴指向飞行方向,ObZb轴指向地心,ObYb轴指向根据右手定则确定。星体坐标系是星上几何参考基准,推力器安装方位、卫星质心等均以此为参考;
(2)质心坐标系OmXmYmZm:原点Om位于星体质心,三轴指向与星体坐标系相同;
(3)轨道坐标系OoXoYoZo:原点Oo位于星体质心,OoZo轴由星体质心指向地心,OoXo位于轨道平面内,垂直于OoZo轴且沿向飞行方向,OoYo轴指向根据右手定则确定。
本文所有参量均在星体坐标系ObXbYbZb下定义。
2.2 卫星姿态动力学模型
假设卫星采用偏置动量控制方式,卫星配置n个推力器、p个飞轮和q个磁力矩器,卫星采用陀螺测量三轴角速度。卫星角动量[11]可以表示为
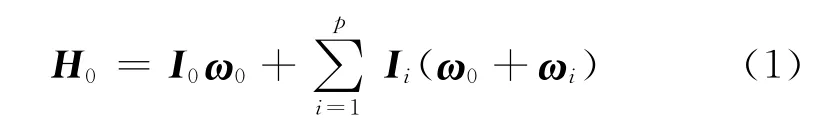
式中:I0为卫星转动惯量矩阵(包括飞轮);ω0为星体角速度;Ii为第i个飞轮的绕自身转轴的转动惯量矩阵;ωi为第i个飞轮相对于星体的角速度。
根据角动量定理,可得
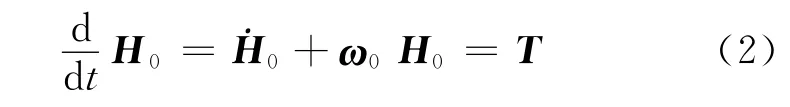
式中:T为除飞轮控制力矩以外卫星受到的其他所有外力矩之和,本文模型中指推力器和磁力矩器引起的力矩,则有

式中:ri为第i个推力器喷口中心点坐标,rm为卫星质心坐标,Fi为第i个推力器的推力矢量,τi为第i个磁力矩器产生的卸载力矩,ῶ0为角速度ω0的叉乘操作数,对于ω0=有ῶ0=
将式(1)代入式(3)可得

即
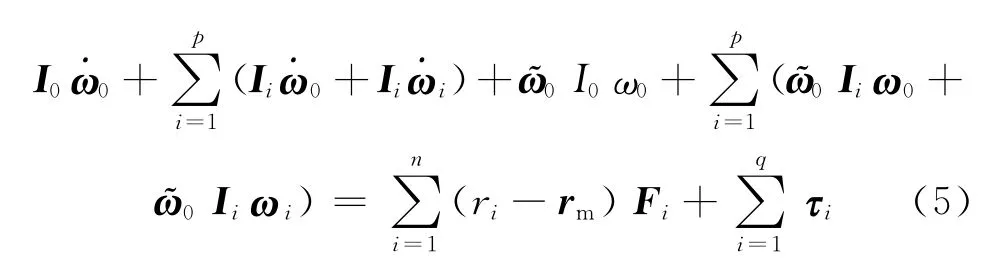
式(5)中Ii、ω0和˙ω0量级均较小,因此其乘积项可以忽略,由式(5)简化可得
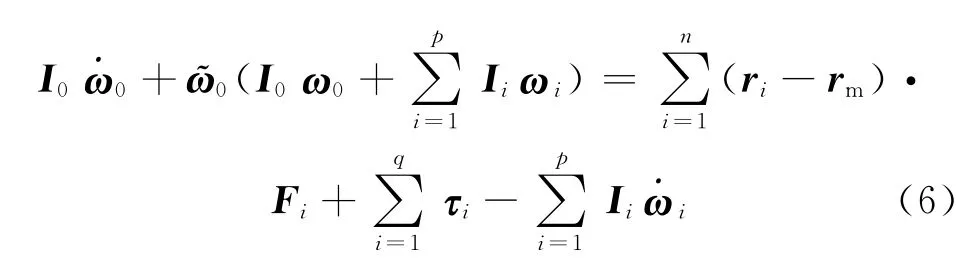
3 质量特性计算方法
式(6)中共含有9个未知数:Ⅰ0xx、Ⅰ0yy、Ⅰ0zz、Ⅰ0xy、Ⅰ0xz、Ⅰ0yz、rmx、rmy、rmz,耦合关系强,计算复杂;文献[2-3]等假设星体运动足够慢,从而忽略ῶ0、I0、ω0项来简化模型,但同时也降低了计算精度。本文提出一种基于交互式迭代和批量最小二乘法的计算方法,先给定卫星转动惯量初值,根据I00计算r1m,然后根据计算,再根据I10计算r2m…… 以此类推,最终算法收敛可以得出I0和rm;每一步计算都使用多元线性批量最小二乘回归算法,其标准形式[12]为

式中:A为由已知量组成的参数矩阵,x为待求解未知向量,b为无噪声测量已知量,ξ为测量噪声矢量。最小二乘算法的目标是求解,使得-b平方和达到最小。对于式(7)所示的标准形式可以直接使用批量最小二乘算法求解:
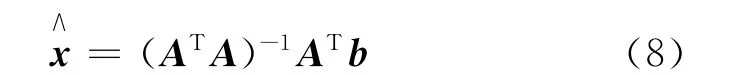
本文算法的核心就是将式(6)的姿态动力学方程转化成式(7)的标准形式,并通过式(8)的模式进行求解。
本文提出的批量最小二乘法与文献[10]提出的递归最小二乘法相比,可以适用于在轨不进行连续大角度姿态机动的卫星。这类卫星只在地球捕获等工况进行间歇喷气姿态调整,推力器单次喷气时间约为几十至几百毫秒,而喷气间隔时间可达几秒、十几秒甚至几十秒,如使用递归算法,往往会由于相邻帧数据中含有不喷气的无效数据而导致ATA病态,无法求逆。
3.1 质心坐标计算方法
质心坐标计算时假设I0为已知,由式(6)可得
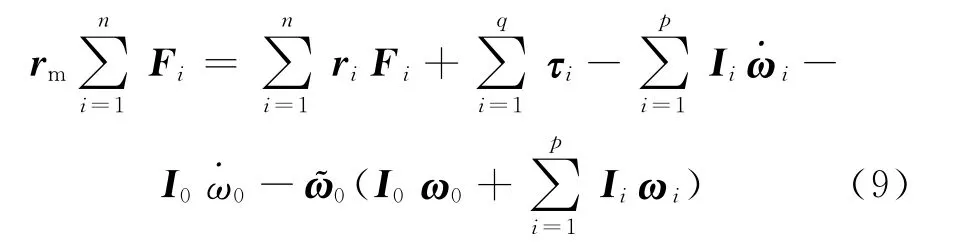
根据矩阵叉乘交换律有
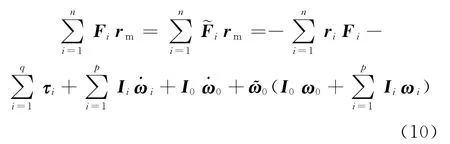
其中~Fi为Fi的叉乘操作数,对于
令

则根据(8)式可以求解质心坐标rm。
3.2 转动惯量矩阵计算方法
转动惯量计算时假设质心rm为已知,根据式(6)有

接下来对I0˙ω0和ῶ0I0ω0两项进行转化:


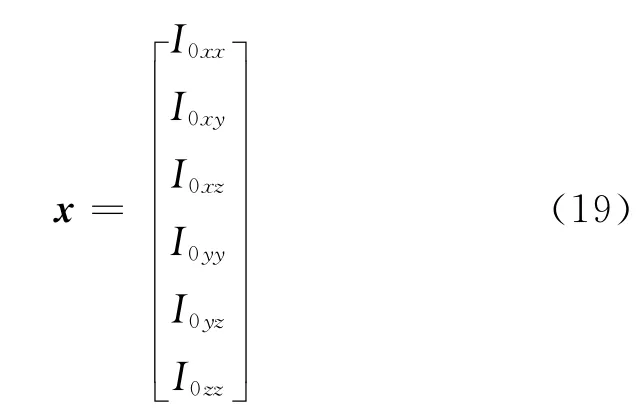
综合式(15)、式(18)和式(19)即可利用批量最小二乘法求出x,即求卫星转动惯量矩阵中的6个未知参数。
4 在轨数据分析与验证
利用某卫星在轨实际飞行数据对本文算法进行验证,通过Matlab仿真软件进行数值仿真。验证状态选取为星箭分离后卫星进行地球捕获的工况,此工况下卫星绕三轴均有角速度分量,姿控推力器虽为间歇喷气,但会在三轴上均产生角加速度。
卫星姿控推力器喷口中心点位置和安装角度见表1,其中安装角度指推力器轴线(沿羽流方向)与星体坐标系三轴的夹角;推力指向如图1所示。卫星陀螺角速度和推力器喷气累计时间见表2。

表1 卫星姿控推力器指向及喷口中心点坐标Table 1 Directions and coordinates of attitude control thrusters

图1 卫星姿控推力器推力指向示意图Fig.1 Directions of attitude control thrusters
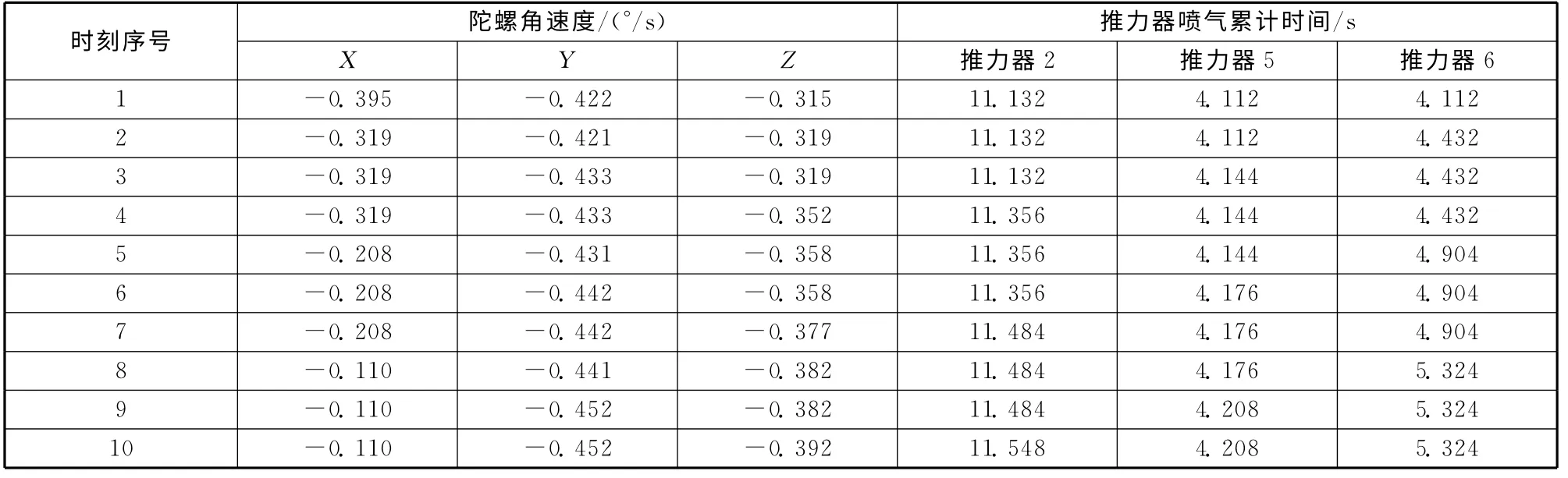
表2 陀螺角速度和推力器喷气累计时间Table 2 Angular velocity of gyro and accumulative working-time of attitude control thrusters
根据地面质量特性测试结果推算和根据本文件算法计算的在轨质量特性参数对比见表3。
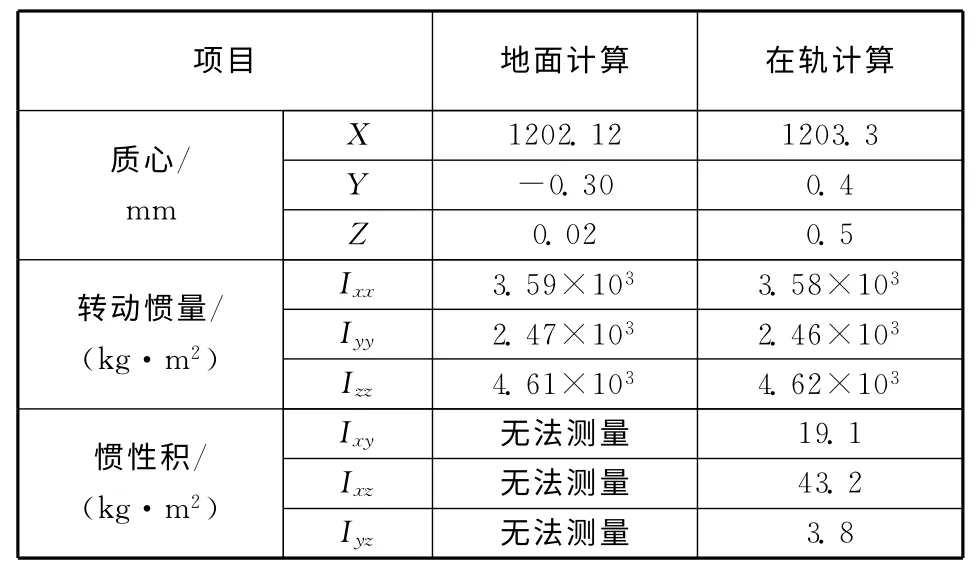
表3 地面与在轨质量特性计算结果对比Table 3 Results of measurement and calculation
在轨计算结果与地面计算结果略有差异,但非常相近,综合考虑两种计算过程的误差(包括地面测量系统误差、太阳翼展开模型和推进剂微重力模型与真实状态差异、卫星在轨姿态机动引起推进剂晃动等),可以认为本文提出的算法正确并具备较高精度。
当初值取为I0=时,质心坐标收敛曲线分别如图2~图4所示,转动惯量和惯性积收敛曲线如图5~图10所示,本文算法具有较快的收敛特性,在迭代500次左右时就已经完全收敛。
此外本文算法对于初值选取有一定的适应性。
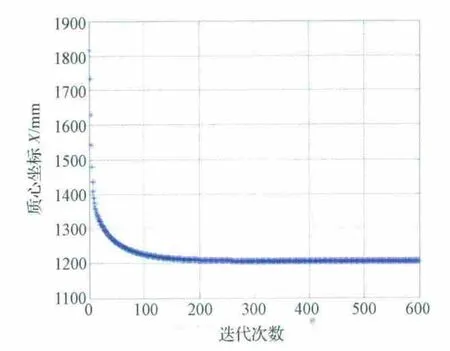
图2 质心坐标X 收敛曲线Fig.2 Curve of centroid in Xdirection

图3 质心坐标Y 收敛曲线Fig.3 Curve of centroid in Y direction
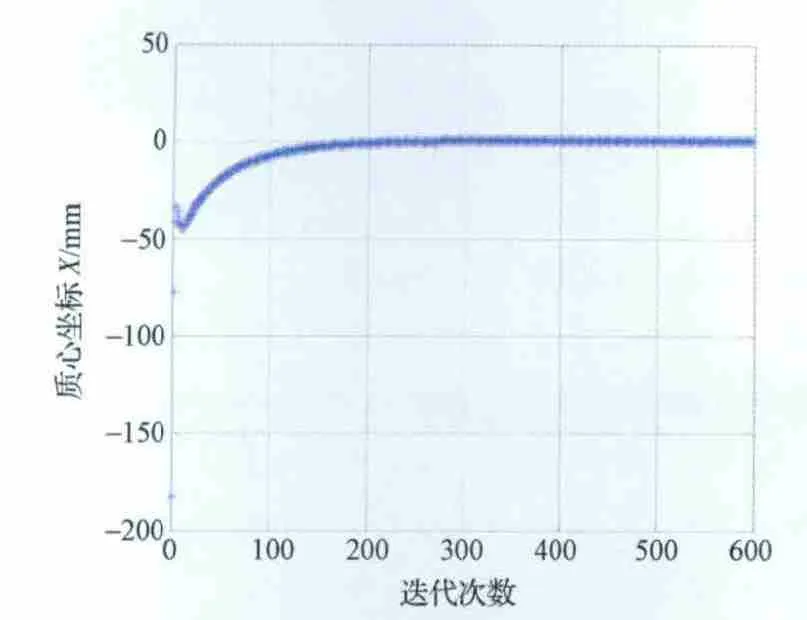
图4 质心坐标Z 收敛曲线Fig.4 Curve of centroid in Zdirection
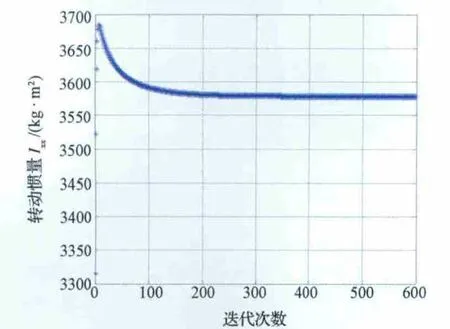
图5 转动惯量Ⅰxx收敛曲线Fig.5 Curve of Ⅰxx

图6 转动惯量Ⅰyy收敛曲线Fig.6 Curve of Ⅰyy

图7 转动惯量Ⅰzz收敛曲线Fig.7 Curve of Ⅰzz

图8 惯性积Ⅰxy收敛曲线Fig.8 Curve of Ⅰxy

图9 惯性积Ⅰzx收敛曲线Fig.9 Curve of Ⅰzx
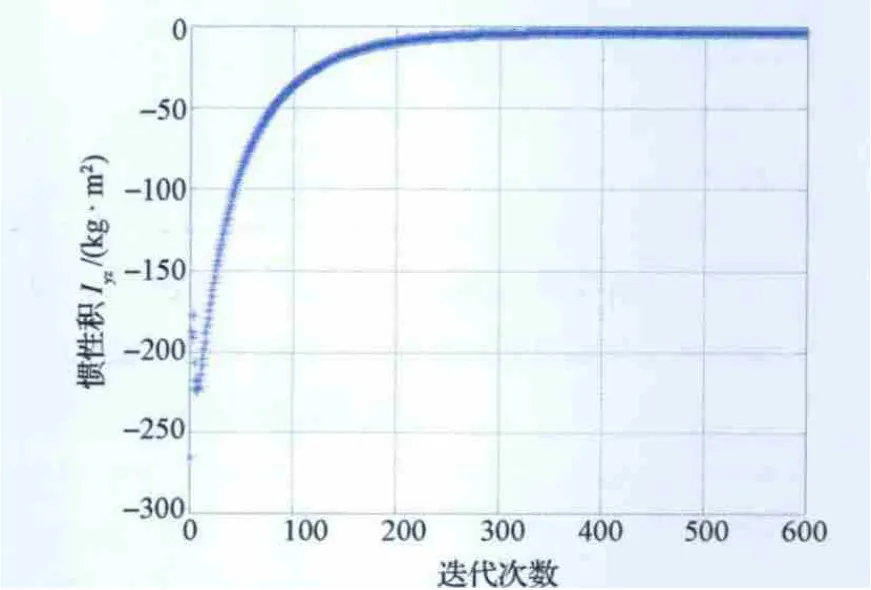
图10 惯性积Ⅰyz收敛曲线Fig.10 Curve of Ⅰyz

图11 不同初值选取情况下收敛特性对比Fig.11 Curve of different initial value
5 结束语
准确获取质量特性参数,是卫星实现高精度姿态控制进而完成复杂空间任务的基础。基于敏感器和执行机构的在轨质量特性计算方法,能够实现全真实状态下、全生命周期的质量特性实时计算。本文提出的卫星在轨质量特性计算方法,对卫星姿态传感器配置要求低,对卫星控制模型适应性强,对动力学模型参数耦合关系考虑充分,对卫星在轨运动状态要求低,适用范围更广泛。通过某卫星实际在轨遥测数据的计算,结果表明,此方法计算精度高,收敛快速、稳定,可为卫星在轨高精度轨道和姿态控制提供参考。
(References)
[1]王洪鑫,徐在峰,赵科,等.航天器质量特性测试技术新进展[J].航天器环境工程,2011,28(2):171-174
Wang Hongxin,Xu Zaifeng,Zhao Ke,et al.Recent advances of mass property measuring technology for spacecraft[J].Spacecraft Environment Engineering,2011,28(2):171-174(in Chinese)
[2]Bergmann E V,Walker B K,Levy D R.Mass property estimation for control of asymmetrical satellites [J].Journal of Guidance,Control,and Dynamics,1987,10(2):483-492
[3]Bergmann E V,Dzielski J.Spacecraft mass property identification with torque-generating control[J].Journal of Guidance,Control,and Dynamics,1990,13(2):99-103
[4] Wilson E,Lages C,Mah R.On-line,gyro-based,mass-property identification for thruster-controlled spacecraft using recursive least squares[C]//The 45thMidwest Symposium on Circuits and Systems.New York:IEEE,2002
[5]Wilson E,Sutter D W. Motion-based mass and thruster-property identification for thruster-controlled spacecraft,AIAA 2005-6907[C]//AIAA Infotech Aerospace Conference.Washington D.C.:AIAA,2005
[6]Tanygin S,Williams T.Mass property estimation using coasting maneuvers[J].Journal of Guidance,Control,and Dynamics,1997,20:625-632
[7]Kim J,Agrawal B N.System identification and automatic mass balancing of ground-based three-axis spacecraft simulator,AIAA 2006-6595[C]// AIAA Guidance,Navigation,and Control Conference and Exhibit.Washington D.C.:AIAA,2006
[8]Kim J,Agrawal B N.Automatic mass balancing of airbearing-based three-axis rotational spacecraft simulator[J].Journal of Guidance,Control,and Dynamics,2009,32(3):1005-1017
[9]徐文福,何勇,王学谦,等.航天器质量特性参数的在轨辨识方法[J].宇航学报,2010,31(8):1906-1914
Xu Wenfu,He Yong,Wang Xueqian,et al.On orbit identification of mass characteristic parameters for spacecraft[J].Journal of Astronautics,2010,31(8):1906-1914(in Chinese)
[10]王书廷,曹喜滨.卫星质量特性的在线辨识算法研究[C]//第25 届中国控制会议.北京:中国自动化学会,2006:519-524
Wang Shuting,Cao Xibin.On-line mass-property identification algorithm research for satellite [C]//Proceedings of the 25thChinese Control Conference.Beijing:Chinese Association of Automation,2006:519-524(in Chinese)
[11]屠善澄.卫星姿态动力学与控制[M].北京:中国宇航出版社,1999
Tu Shancheng.Satellite attitude dynamics and control[M].Beijing:China Astronautics Press,1999 (in Chinese)
[12]张贤达.矩阵分析与应用[M].北京:清华大学出版社,2004
Zhang Xianda.Matrix analysis and application[M].Beijing:Tsinghua University Press,2004(in Chinese)

