板钢筋应力状态对框架梁受力影响的数值模拟分析

邓 然

(重庆大学土木工程学院，重庆 400045)

钢筋混凝土框架结构由于具有用料经济、耐久性好、可灵活地配合建筑平面布置等优点，在我国得到了广泛的应用，成为近年来城乡建设中住宅、办公楼、学校等建筑优先采用的结构形式。根据施工方法不同，可分为现浇混凝土框架结构、装配式框架结构和装配整体式框架结构。这其中，现浇混凝土框架结构由于在节点处将柱、梁、楼板整体现浇到一起，使得结构的整体性较好，刚度大，抗震性能好，且随着施工水平的进步，现浇混凝土框架施工已非常方便，构件可灵活浇筑成各种形状和尺寸，故目前大多数混凝土框架结构都采用现浇的方式。

1 现浇楼板对框架梁受力的影响

试验研究表明［1-2］，楼板与框架梁现浇在一起形成整体，板可以看做梁的翼缘，增大了梁的截面和刚度;且框架梁两侧的板内配有与框架梁纵轴线平行的板顶钢筋和板底钢筋，这两层板内钢筋在一定程度上参与梁端受力，对框架梁端正截面受弯承载力有明显贡献;故由于现浇板与框架梁的共同作用，使得梁端实际承载能力得到提高。

2008年汶川地震发生后，对框架结构震害的调查发现，虽然已按照《建筑抗震设计规范》(GB50011-2001)［3］对“强柱弱梁”的要求做了设计，但很多现浇框架结构仍旧出现了柱端破坏的震害，几乎没有发现出现梁铰机制的框架。出现这种现象的主要原因之一就是由于现浇楼板对框架梁刚度和承载力的贡献，使得梁端实际受弯承载能力增强［4］。现浇楼板对框架梁刚度的增大作用，在设计过程中按照《混凝土结构设计规范》(GB50010-2010)［5］的要求将梁刚度乘以放大系数来考虑，故影响框架梁端受弯承载力的主要因素为框架梁两侧一定宽度内楼板中的钢筋参与抵抗负弯矩，这相当于增加了框架梁的负弯矩筋，显著增强了框架梁的抗负弯矩能力。按照我国规范，目前的作法是将按纯框架(即没有楼板)设计的梁刚度考虑楼板翼缘作用予以增大，然而在设计截面时却把梁钢筋全面集中在矩形梁截面内，而板内钢筋另配，造成了框架梁端实际受拉钢筋超配，从而使得框架梁实际受弯承载力显著增强，甚至超过柱端受弯承载力，致使框架结构无法实现“强柱弱梁”的梁铰破坏机制。

我国现行的《建筑抗震设计规范》(GB50011-2010)［6］针对这种现象，提高抗震设计时采用的框架柱端弯矩增大系数，通过这种方式加强了“强柱弱梁”的控制力度。但蔡龙等人［7］的研究表明，有限地提高柱端弯矩增大系数并不能取得明显的效果，除非该增大系数取的很大，但这种做法又会使框架柱的设计极为不经济。要想框架结构实现梁铰式破坏机制，应从根本上减小梁端过大的受弯承载能力，即减少框架梁端及两侧一定范围内的楼板截面中“超配”的受拉钢筋。

王依群等人认为，计算梁刚度时考虑了梁侧楼板的贡献，故梁的内力和钢筋已包括了梁侧楼板的内力和钢筋，因此梁钢筋不应全部放在梁的矩形截面内，而应有一部分放在梁侧的楼板内，文献［8］针对2个8度二级抗震框架结构，将与楼板现浇的梁上部纵筋减小30%，分配到楼板中去，同时从楼板钢筋中扣除相应的量，对罕遇地震作用下的2个实际工程进行弹塑性时程计算，结果表明可改善框架结构的抗震性能。至于板内钢筋能减少多少，梁端T形截面中的受拉钢筋应怎样进行合理的配置，尚无明确的定论。

2 板内钢筋应力状态

框架结构现浇楼板中的钢筋在地震未发生时，主要承担竖向荷载。由结构内力分布可知，在板跨中，竖向荷载引起的内力使板下部钢筋受拉，上部钢筋受拉;在靠近框架梁的位置，板上部钢筋受拉，下部钢筋受压。水平地震作用下，在框架梁上部受拉一端，梁矩形截面与两侧一定宽度的楼板共同组成T形截面，由于板截面高度相比梁截面高度较小，板内上层和下层钢筋一般都位于T形截面中和轴之上，故上下钢筋都与梁内钢筋一起共同抵抗负弯矩而受拉。地震来临时，板内上层钢筋中应已经存在先前竖向荷载引起的拉应力，下层钢筋中应已经存在竖向荷载引起的压应力。这一部分已有的应力对板内钢筋参与抵抗梁端负弯矩的程度有无影响，有多大的影响，是必需解决的问题。只有了解清楚板内钢筋的应力状态，才能知道楼板钢筋对框架梁端负弯矩承载力的贡献有多大，才可进一步为合理调整框架梁端配筋量提供理论依据，真正从根本上实现“强柱弱梁”。

为探究板内钢筋应力状态对框架梁受力性能有无影响，本文采用非线性有限元软件ABAQUS建立3个带楼板翼缘框架梁悬臂模型，分别对板内钢筋预先施加不同的应力状态并进行数值模拟，对比其分析结果，得出了楼板内钢筋在3种应力状态下对框架梁受力性能的影响，以及如何合理调整梁端截面钢筋配置的建议。

3 有限元模型说明

3.1 尺寸和配筋

采用带楼板翼缘的框架悬臂梁模型，其中，梁跨长3 m，梁截面尺寸为250 mm×600 mm;楼板厚度取120 mm，楼板宽度按照文献［9］的建议选取梁每侧6倍板厚作为板的有效宽度，如图1所示。

图1 有限元模型示意图

根据一般民用建筑荷载情况得到构件配筋如下:梁内底部纵筋采用318，顶部钢筋采用220和125，箍筋为8@200;梁两侧楼板上层、下层配筋均为双向8@120。

3.2 材料性能

3.2.1 混凝土

针对混凝土复杂多变的强度和变形性能，国内外学者基于不同的理论模型建立了多种本构关系，本文选用混凝土规范［5］建议的本构关系。

大型有限元程序ABAQUS提供的模拟混凝土的本构模型有3种:弥散裂缝模型、开裂模型和损伤塑性模型。本文采用损伤塑性模型(Concrete Damaged Plasticity Model)，该模型可以通过定义受拉、受压损伤变量dt和dc来考虑混凝土的拉、压损伤。为了防止体积自锁，混凝土的单元类型采用八节点减缩积分实体单元 C3D8R。混凝土弹性模量取3.02×104MPa，泊松比取0.2，单轴抗压强度取22.6 MPa，单轴抗拉强度取2.49 MPa。

3.2.2 钢筋

本文选用的钢筋本构关系采用理想弹塑性模型，即双直线模型，钢筋材料力学性能指标见表1。在ABAQUS中，采用三维桁架线性单元T3D2模拟钢筋。钢筋与混凝土之间的相互接触关系通过*EMBEDDED ELEMENT(内部嵌入)来进行模拟，该方法除了可以通过在inp文件进行定义外，还可以在ABAQUS/CAE中进行直接定义，并能在ABAQUS的后处理模块Visualization中直观显示钢筋的应力、应变等相关变量随着分析步的变化。

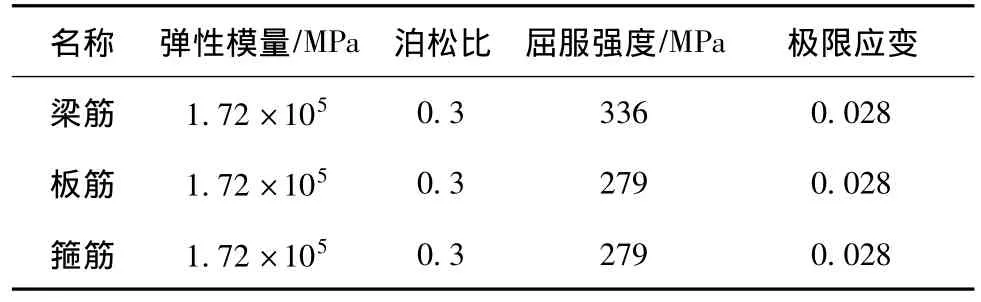
表1 钢筋材料力学性能指标

3.3 模型设置与加载方式

建立3个模型，分别命名为M1、M2和M3，均在一端施加约束成为固端，采用位移加载方式，在自由端施加竖直向下的位移。对M1的板内钢筋不做任何处理;对M2的板内上层钢筋施加大小等于材料屈服强度的初始拉应力，以模拟现浇板上层钢筋在竖向荷载下刚好受拉屈服的临界状态，下层钢筋不作任何处理;对M3的板内上层钢筋施加大小等于材料屈服强度的初始拉应力，板内下层钢筋施加大小等于材料屈服强度的初始压应力，以模拟现浇板上层和下层钢筋在竖向荷载下刚好受拉屈服和受压屈服的临界状态。

根据结构力学，梁自由端的竖向位移在固端引起的弯矩使板内钢筋和梁顶部钢筋受拉、梁底部钢筋受压，可简单有效地模拟水平地震作用下框架梁端钢筋所处的应力情况;将模型中的板内钢筋初始应力状态设为理想临界应力状态，容易得出结果，便于观察现象，可从总体上了解板内钢筋应力状态对框架梁在地震作用下受力性能的影响。

4 结果分析

4.1 荷载-位移曲线分析

模型M1、M2、M3最后达到的最大荷载分别为203 kN、164 kN和164 kN，对应的自由端竖向位移分别为19 mm，15 mm和16 mm。3个模型的荷载-位移曲线如图2所示。

图2 3个模型的荷载-位移曲线

未对楼板钢筋施加初始应力的框架梁(即模型M1)承载能力高于M2和M3，表明楼板钢筋中存在的竖向荷载引起的“初始”应力状态对水平地震作用下的框架梁承载能力有一定影响;模型M2和M3的荷载-位移曲线上升段几乎重叠，由于M3中楼板下层钢筋施加的初始应力为压应力，在加载过程中钢筋先受“预压”再受拉，提高了钢筋的延性，但抗拉强度不变，故2个模型的最大荷载差别很小，但最大荷载点之后的曲线下降段M3比M2平缓。

4.2 楼板钢筋应力分析

3个模型中与框架梁平行的楼板上层和下层钢筋在不同竖向位移下，沿着与框架梁垂直(即楼板宽度)方向的应力分布情况如图3～图8所示。其中，横坐标为离框架梁端的距离，纵坐标为楼板钢筋应力，图例为与模型对应的不同竖向位移值。

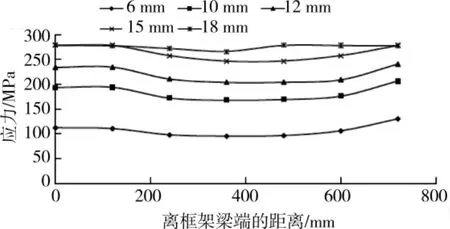
图3 M1板上层钢筋应力分布图

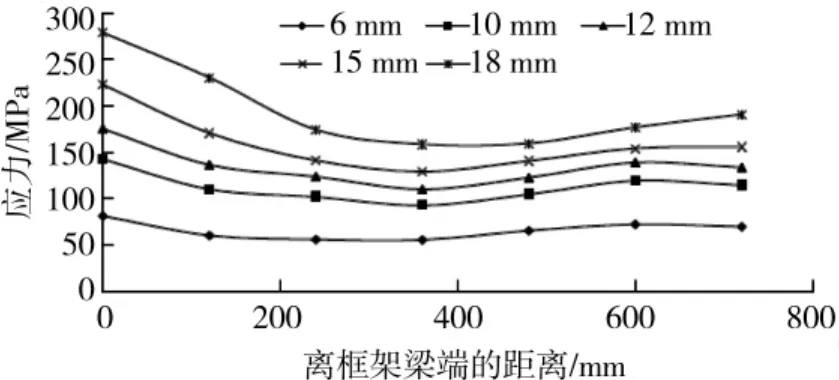
图4 M1板下层钢筋应力分布图

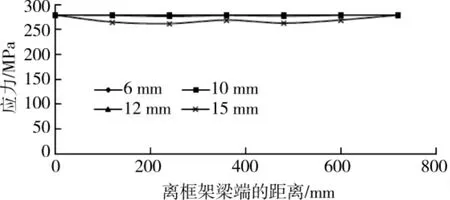
图5 M2板上层钢筋应力分布图

图6 M2板下层钢筋应力分布图

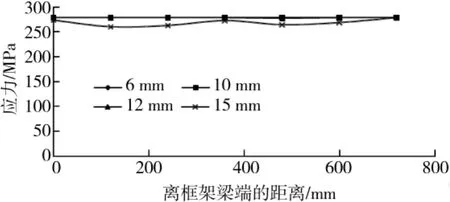
图7 M3板上层钢筋应力分布图

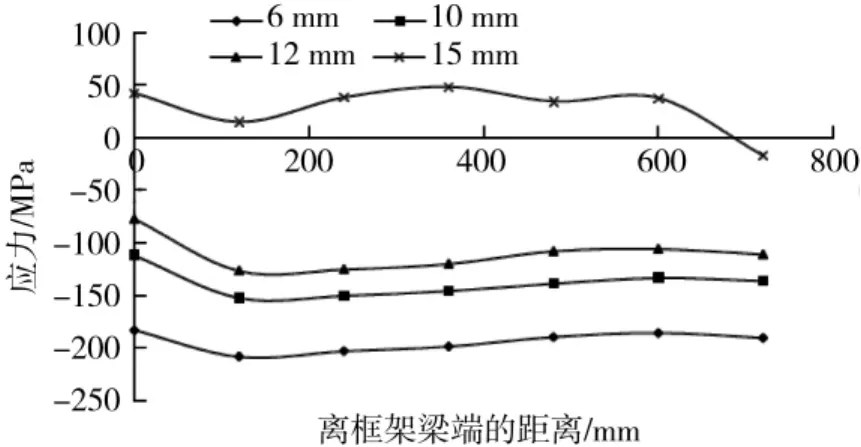
图8 M3板下层钢筋应力分布图

从图3、图5、图7可以看出，M1板内上层钢筋应力随着竖向位移增大而增大，位移为15 mm时靠近框架梁端的钢筋应力达到屈服值，位移为18 mm时上层钢筋基本上全部屈服;M2和M3板内上层钢筋由于施加了大小等于材料屈服强度的初始拉应力，在位移增大过程中其应力值始终保持在屈服水平，说明上层钢筋在竖向荷载引起的应力状态下仍能在后续加载过程中参与受拉(钢筋应变不超过材料极限应变的前提下)。从图4、图6、图8可以看出，3个模型板内下层钢筋应力都随着竖向位移增大而增大，M3板内下层钢筋应力由最初的压应力逐渐变为拉应力。对比同一竖向位移下的M1上、下层钢筋应力可看出，沿楼板宽度方向各距离处的上层钢筋应力差别不大，而下层钢筋表现为靠近框架梁端处的应力值较大，这是因为下层钢筋相较于上层钢筋更靠近中和轴，截面弯矩所产生的拉力较上层钢筋小，故只有靠近框架梁端的下层钢筋发挥较大的作用，产生较大拉应力，因而不象上层那样所有钢筋都能充分发挥抗拉性能;而M2和M3下层钢筋在同一竖向位移下沿楼板宽度方向的应力变化没有M1明显(但仍能看出靠近框架梁端的钢筋应力最大)，这是由于M2和M3中的板内上层钢筋已初设为达到屈服状态，故在受力过程中需要更多的下层钢筋参与受拉，这也可解释在图6中M2板内下层钢筋应力在相同竖向位移条件下比图4中M1板内下层钢筋应力稍高的现象。

4.3 框架梁受拉钢筋应力分析

图9给出了3个模型框架梁顶部纵向受拉钢筋应力随竖向位移值的变化曲线。对比图中钢筋应力情况可得出:M2和M3的曲线几乎相同，且纵向受拉钢筋先于M1的纵向受拉钢筋进入屈服阶段，说明板内上层钢筋中由竖向荷载引起的“初始”拉应力对框架梁钢筋受力有一定影响，而板内下层钢筋中由竖向荷载引起的“初始”压应力则影响不大。

图9 不同竖向位移下框架梁受拉钢筋应力曲线

5 讨论

从荷载-位移曲线和框架梁受拉钢筋应力曲线可知，板内钢筋由竖向荷载引起的应力状态对框架梁在水平地震作用下的承载能力有降低的影响，且使得框架梁受拉钢筋提前进入屈服阶段，其中处于拉应力状态的上层钢筋对承载力影响作用较大，处于压应力状态的下层钢筋对承载力大小没有太大影响，但可适当提高框架梁延性。

从楼板钢筋应力随加载过程的变化可知，由于与中和轴距离较远，板内上层钢筋参与框架梁端抗拉的程度较大，基本上有效楼板宽度范围内所有上层钢筋都能达到屈服，而下层则表现为框架梁端两侧的钢筋发挥较大贡献。在上层钢筋处于拉应力状态下，下层钢筋参与抗拉程度增加，不同楼板宽度处的钢筋应力差别减小，但位于框架梁端两侧附近的钢筋仍对抗拉贡献最大。

为解决实际地震中无法实现“强柱弱梁”的问题，可借鉴国外的一些规范和王依群等人的建议［8］，将一部分梁内钢筋移置到两侧楼板中去同时从楼板钢筋中扣除相应的量。由本文分析结果可知，在竖向荷载引起的应力状态下，仍是板内上层钢筋和下层钢筋中靠近梁段两侧的部分参与受拉程度最大，故将梁内钢筋部分移置到楼板上层及下层靠近梁端位置，并扣除这些位置处楼板钢筋相应的量，效果较好，既可减小框架梁端超配的钢筋，又能保证这部分移置到楼板的钢筋仍能发挥较大作用，又能保证承载能力下降太多。

为了突出对比，本文模拟的钢筋在竖向荷载作用下的应力状态均取为屈服水平，而实际情况下大多数板内钢筋在竖向荷载下未进入屈服阶段，故板内钢筋应力状态对框架梁的真实影响应比本文模拟结果偏小，具体板内钢筋在各种应力状态下对框架梁受力性能的影响有待进一步研究;且本文为初步探讨板内钢筋应力状态对框架梁在水平地震作用下的受力影响，为了便于得到结论和观测现象，采用简单的悬臂梁自由端单向位移加载方式，虽在一定程度上可以模拟楼板和梁内钢筋受拉，但构件在地震作用下的具体反应还需进一步采取反复加载方式和弹塑性时程分析才能得到。

6 结语

现浇楼板中的钢筋在地震未发生时主要承担竖向荷载，板内上、下层钢筋具有不同的应力状态。已有应力状态的板钢筋使得框架梁在水平地震作用下的承载能力下降，梁受拉钢筋提前进入屈服阶段。其中处于拉应力状态的上层钢筋影响作用较大，下层钢筋中靠近框架梁端两侧的部分相比其他位置参与梁端负弯矩抗拉程度较大。在竖向荷载引起的应力状态下，将梁内钢筋部分移置到楼板上层及下层靠近梁端位置效果较好，既可减小框架梁端超配的钢筋，又能保证这部分移置到楼板的钢筋发挥较大作用又不会导致承载能力下降太多影响结构的安全性。

［1］蒋永生，陈忠范，周绪平，等.整浇梁板的框架节点抗震研究［J］.建筑结构学报，1994(6):11-16.

［2］杨迎春，吴照学.RC框架结构“强柱弱梁”破坏机制探讨［J］.合肥学院学报:自然科学版，2011(4):80-82.

［3］GB50011-2001.建筑抗震设计规范［S］.

［4］马千里，叶列平，陆新征.现浇楼板对框架结构柱梁强度比的影响研究［M］//汶川地震建筑震害调查与灾后重建分析报告.北京:中国建筑工业出版社，2008:263-271.

［5］GB50010-2010.混凝土结构设计规范［S］.

［6］GB50011-2010.建筑抗震设计规范［S］.

［7］蔡龙，杜宏彪，金仁和.新旧建筑抗震设计规范关于“强柱弱梁”的对比和分析［J］.工程抗震与加固改造，2012(2):36-40.

［8］王依群，韩鹏，韩昀珈.梁钢筋部分移置梁侧楼板的现浇混凝土框架抗震性能研究［J］.土木工程学报，2012(8):55-66.

［9］吴勇，雷汲川，杨红，等.板筋参与梁端负弯矩承载力问题的探讨［J］.重庆建筑大学学报，2002，24(3):33-37.