四元数调制重叠变换及其在双彩色图像数字水印中的应用

陈北京 田翠翠 戴 慧 王定成 舒华忠

(1南京信息工程大学计算机与软件学院,南京 210044)

(2南京信息工程大学江苏省网络监控工程中心,南京 210044)

(3南京工程学院计算机工程学院,南京 210013)

(4东南大学影像科学与技术实验室,南京 210096)

著名数学家Hamilton[1]提出的四元数(quaternions)是传统复数的推广, 1个四元数包含1个实部和3个虚部.20世纪90年代,国内外部分学者开始将四元数的相关理论引入到彩色图像处理中[2-6],将彩色图像的每个像素值采用1个纯四元数来表示,3个分量作为其3个虚部.基于四元数彩色图像表示方法,很多经典的针对灰度图像的算法和工具都已经有效推广应用于彩色图像处理中,特别是一些常用的数学变换,如Fourier变换[2]、小波变换[3]、Gabor变换[4]、Curvelet变换[5]和矩变换[6]等.研究结果表明,该表示方法维护了三通道的整体性,考虑了色彩关联,能够有效避免现有彩色图像常用处理方法(灰度化和三通道分别处理)的不足,即丢失了色彩信息和破坏了三通道的整体性.

复数调制重叠变换(modulated complex lapped transform, MCLT)是将调制重叠变换(modulated lapped transform, MLT)由实数域向复数域扩充得到的[7].MCLT系数与MLT系数具有相同的幅度,但前者较后者增加了相位信息.MCLT具有完全重建、无边界效应和较高的编码增益等优良特性,已广泛应用于音频处理、数字水印、去噪和身份鉴别等诸多领域[7-8].

本文定义了一种四元数调制重叠变换(modulated quaternion lapped transform, MQLT),将MCLT变换由复数域向四元数域扩充,以处理四元数信号(特别是彩色图像).通过建立彩色图像MQLT系数和三通道MCLT系数之间的关系,提出针对MQLT变换的有效计算方法.通过分析MQLT系数的相关性质,将MQLT变换应用于彩色图像数字水印中,提出鲁棒的双彩色图像盲水印算法.

1 四元数及MCLT

1.1 四元数及四元数彩色图像表示方法

一个四元数q可以表示为

q=a+bi+cj+dk

(1)

式中,a,b,c,d∈R;i, j, k为虚数单位,且满足如下运算法则:

i2=j2=k2=-1
ij=-ji=k
jk=-kj=i
ki=-ik=j

(2)

以RGB颜色空间为例,彩色图像f(m,n)可以表示为

f(m,n)=fR(m,n)i+fG(m,n)j+fB(m,n)k

(3)

式中,fR(m,n),fG(m,n),fB(m,n)分别为彩色图像的红、绿、蓝3个分量.

由式(3)可知,1幅彩色图像可表示为1个纯四元数矩阵.对于采用其他颜色空间表示的彩色图像,比如CIE XYZ，HSV，YUV等,只需替换式(3)中相应的3个虚部即可.

1.2 MCLT

令f(x,y)为1个2M×2N的二维图像密度函数,其MCLT定义为[7]

jpS(x,y,U,V)]

(4)

式中

(5)

(6)

令FC(U,V)和FS(U,V)分别表示F(U,V)的实部和虚部,由式(4)～(6)易得如下的对称性或反对称性公式:

fC(2M-1-U, 2N-1-V)=(-1)M+NFC(U,V)

fC(2M-1-U,V)=(-1)M+1FC(U,V)

fC(U,2N-1-V)=(-1)N+1FC(U,V)

fS(2M-1-U,2N-1-V)=(-1)M+NFS(U,V)

fS(2M-1-U,V)=(-1)MFS(U,V)

fS(U,2N-1-V)=(-1)NFS(U,V)

U=0,1,2,…,M-1;V=0,1,2,…,N-1

(7)

因此,逆变换IMCLT可定义为

jpS(x,y,U,V)]

(8)

2 四元数调制重叠变换及其应用

2.1 定义

根据灰度图像MCLT的定义式(4)和四元数代数理论,令大小为2M×2N的彩色图像f(m,n)的右边型四元数调制重叠变换MQLT变换及其逆变换IMQLT分别为

μpS(m,n,U,V)]

(9)

μpS(m,n,U,V)]

(10)

由式(2)可知,四元数的乘法不满足交换律,因此交换式(9)累加项中两项的位置,将pC(m,n,U,V)-μpS(m,n,U,V)移到f(m,n)的左边,可以定义左边型MQLT及相应的左边型IMQLT.本文中讨论的都是右边型MQLT,左边型MQLT可以类似分析.

2.2 系数特性及有效计算

MQLT和IMQLT可由单通道传统的MCLT及其逆变换IMCLT表示.下面分别给出μ=k和μ=μLum时的关系式,并据此提出MQLT的有效快速计算算法以及分析MQLT系数的相关特性.

当μ=k时,将式(3)代入式(9)可得

fB(m,n)k][pC(m,n,U,V)-kpS(m,n,U,V)]=

fG(m,n)pS(m,n,U,V)]+

fR(m,n)pS(m,n,U,V)]+

A(U,V)+B(U,V)i+C(U,V)j+

D(U,V)k

(11)

式中

A(U,V)=-Im(MCLT(fB)(U,V))

B(U,V)=Re(MCLT(fR)(U,V))+
Im(MCLT(fG)(U,V))

C(U,V)=Re(MCLT(fG)(U,V))-
Im(MCLT(fR)(U,V))

D(U,V)=Re(MCLT(fB)(U,V))

(12)

式中,MCLT(fR), MCLT(fG),MCLT(fB)分别为红、绿、蓝通道传统的MCLT系数.

式(11)和式(12)提供了一种关于MQLT变换的有效快速计算方法,即将MQLT变换的计算转换为3个通道MCLT变换的计算.目前,对于MCLT变换的快速计算已有广泛研究[8-9],将这些快速算法与式(11)和式(12)相结合即可实现MQLT变换的有效快速计算.

另外,由式(11)可知,MQLT频域空间是一个四维空间.由式(12)和MCLT系数的对称性可得MQLT系数4个分量的对称性和反对称性分别为

A(2M-1-U,2N-1-V)=(-1)M+NA(U,V)

A(2M-1-U,V)=(-1)MA(U,V)

A(U,2N-1-V)=(-1)NA(U,V)

B(2M-1-U,2N-1-V)=(-1)M+NB(U,V)

C(2M-1-U,2N-1-V)=(-1)M+NC(U,V)

D(2M-1-U,2N-1-V)=(-1)M+ND(U,V)

D(2M-1-U,V)=(-1)M+1D(U,V)

D(U,2N-1-V)=(-1)N+1D(U,V)

U=0,1,2,…,M-1;V=0,1,2,…,N-1

(13)

对于IMQLT,类似可得

C(U,V)j+D(U,V)k][pC(m,n,U,V)+

pC(m,n,U,V)-D(U,V)pS(m,n,U,V)]+

C(U,V)pS(m,n,U,V)]+

B(U,V)pS(m,n,U,V)]+

A(U,V)pS(m,n,U,V)]=

(14)

式中

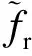
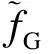
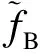
(15)

式中,IMCLT(·)表示传统的MCLT逆变换.

由频域系数的实部A(U,V)和其中一个虚部D(U,V)具有如式(13)所示的(反)对称性可知,Re(IMCLT(A))=0,Im(IMCLT(D))=0,以及

(16)

如果式(9)中取μ=μLum,采用如上所述类似的方法推导可得

fB(m,n)k][pC(m,n,U,V)-

μLumpS(m,n,U,V)]=A(U,V)+

B(U,V)i+C(U,V)j+D(U,V)k

(17)

式中

Im(MCLT(fG)(U,V))+

Im(MCLT(fB)(U,V))]

B(U,V)=Re(MCLT(fR)(U,V))+

Im(MCLT(fB)(U,V))]

C(U,V)=Re(MCLT(fG)(U,V))+

Im(MCLT(fR)(U,V))]

D(U,V)=Re(MCLT(fB)(U,V))+

Im(MCLT(fG)(U,V))] (18)

系数A,B和C同样具有如式(13)所示的(反)对称性.系数D则具有如下特性:

D(2M-1-U,2N-1-V)=(-1)M+ND(U,V)

U=0,1,2, …,M-1;V=0,1,2,…,N-1

(19)

经过IMQLT变换后可得

C(U,V)j+D(U,V)k][pC(m,n,U,V)+

(20)

式中

Im(IMCLT(C))+Im(IMCLT(D))]

Im(IMCLT(C)(m,n))-

Im(IMCLT(D)(m,n))]

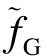
Im(IMCLT(B)(m,n))+

Im(IMCLT(D)(m,n))]

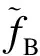
Im(IMCLT(B)(m,n))-

Im(IMCLT(C)(m,n))]

(21)

2.3 基于MQLT的双彩色图像数字水印

2.3.1 嵌入水印前提条件

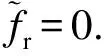
而对于μ=μLum,由式(21)以及Re(IMCLT(A))=0可知,如果按照式(13)的对称性同时修改系数A(u,v)及其对称系数而不修改其余3个系数,即可满足式(16)的前提条件.因此,只可将水印数据嵌入到MQLT系数的1个分量A中.

2.3.2 数字水印算法

结合MQLT变换、Arnold置乱变换以及冗余嵌入策略,将彩色水印重复嵌入到载体图像中,水印算法框图见图1.下面分别从水印嵌入和提取2个方面进行详细阐述.

1) 水印嵌入

令嵌入到彩色载体图像中的彩色图像水印为

图1 彩色图像水印算法框图

w.为了增强算法的鲁棒性(特别是裁剪攻击),采用冗余嵌入策略通过如下步骤重复嵌入KT个水印:

① 水印图像预处理.为了增强水印安全和水印算法的鲁棒性,将KT个水印w进行KI次周期为KP的Arnold置乱,然后将置乱后彩色水印的每个分量十进制像素值转换为8位二进制数据,最终将彩色水印转变为一个比特流水印b.

② 载体图像分块MQLT变换.将彩色载体图像重叠划分成16×16的单位小块,相邻块之间有50%的重叠,然后分别对这些小块进行MQLT变换得到8×8的MQLT系数小块.

③ 水印嵌入.对于每一个8×8宏块,随机选择图2所示的中频候选位置中的部分位置作为水印嵌入区域KM.对于KM中任意一个位置(U,V),针对不同的单位纯四元数(如μLum和k),选择频域系数4个分量(Ah,Bh,Ch和Dh)中的1～4个分量,通过量化索引调制算法[10]嵌入比特流水印b,即

图2 8×8宏块中用于水印嵌入的中频候选位置

(22)

④ 分块IMQLT变换.对所有的单位小块进行IMQLT变换,得到含水印图像.

由此可知,所提算法中的密钥Key主要包括Arnold置乱变换的置乱次数KI和周期KP、中频嵌入位置信息KM、冗余嵌入个数KT以及量化步长KΔ.

2) 水印提取

依据密钥Key,按如下步骤提取水印:

① 测试图像分块MQLT变换.将测试图像按50%区域重叠分成16×16的单位小块,并分别对这些小块进行MQLT变换.

② 提取嵌入的比特流水印.利用密钥Key中的中频嵌入位置信息KM和量化步长KΔ,采用量化解码公式

(23)

提取KT个冗余嵌入的比特流水印bs(s=1,2,…,KT).然后,获取最终比特流水印b′,即

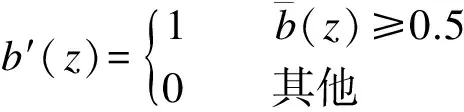
(24)

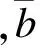
由此可知,水印提取无需原始载体和原始水印,故该操作为盲提取.

3 实验结果与分析

为了验证本文算法的有效性,下面通过一系列实验从不可见性和抗攻击鲁棒性2个方面进行测试.将本文算法与Zhang等[11]提出的基于MCLT的算法进行对比.该算法首先对载体图像进行8×8分块MCLT变换,然后在变换后每个4×4系数宏块的直流系数中嵌入1个比特水印.实验对比中,将本文算法和文献[11]算法分别运用于彩色图像的3个通道中.

3.1 性能评价参数

为了更好地评估算法性能,引入如下2个客观评价参数.

1) 峰值信噪比(peak signal to noise ratio,PSNR).用于评估嵌入水印的不可见性.PSNR值越大,表明嵌入信息的不可见性越好.大小为Mh×Nh的彩色载体图像h和含水印图像h′之间PSNR的计算公式为

PSNR=

(25)

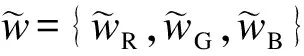
NC=

(26)

3.2 不可见性测试

采用6幅大小为512×512像素的标准图像作为载体图像集,包括经典的Lena、Woman和Peppers等图像(见图3).彩色水印图像则采用了大小为32×32像素的东南大学校徽和Mandrill图像(见图4).

图3 彩色载体图像

图4 彩色水印图像

文献[11]基于MCLT的算法在每个分量的4×4系数宏块中只嵌入1个比特数据,因此最多可在512×512的载体图像中冗余嵌入1.9个32×32的彩色水印.而采用不同单位纯四元数的基于MQLT变换的算法则具有更大的水印容量:对于采用k的算法(记为算法1),如果将图2中所有58个中频位置都选为嵌入区域,则MQLT频域中每个8×8宏块可以嵌入232比特数据,最大可重复嵌入37.4个水印;而对于采用μLum的算法(记为算法2),由于只能在分量A中嵌入水印,故最多可重复嵌入9.3个水印.其他参数设置为:Arnold变换的置乱次数KI=10,量化步长KΔ=80.

采用3种算法在6幅载体图像内嵌入2个不同水印后,所得含水印图像与载体图像之间的PSNR值见表1.采用不同算法将图4(a)嵌入到图3(a)后,所得的含水印图像以及提取的水印见表2.由表可知,不管是从含水印图像的质量还是从算法本身的稳定性来看,算法1和算法2均优于文献[11]算法,这主要是因为后者采用了四元数彩色图像表示方法将彩色载体图像作为一个整体进行处理,而且还考虑了通道之间的关联.此外,算法1的性能优于算法2,可以获取更高质量的含水印图像,并具有更小的PSNRSTD值.这主要是因为算法1完全利用了MQLT系数的4个分量;而算法2只考虑了1个分量,为了嵌入相同的水印数据,需要在每个宏块中修改更多系数,故图像质量退化更厉害.在没有攻击的情况下,算法1和算法2能够完全正确地提取水印,而文献[11]算法则存在偏差.

表1 不同载体图像和不同水印图像的PSNR值

表2 含水印图像和提取的水印

3.3 鲁棒性测试

不可见性和鲁棒性之间相互制约.为了更好地对比和分析不同算法的鲁棒性,选取PSNR值相近的含水印图像进行鲁棒性测试.以表2中文献[11]算法得到的含水印图像(PSNR=31.759 6)为基准,采用算法2嵌入3.2个水印图像4(a)后,得到PSNR值为31.721 5的含水印图像;采用算法1则嵌入4.1个水印,得到PSNR值为31.815 7的含水印图像.对这3幅图像进行各种攻击(包括JPEG压缩、添加噪声、裁剪、滤波以及几何变换等),以测试算法的鲁棒性.表3和表4给出了3种算法针对各种攻击后的实验结果.需要说明的是,这3种算法本身并不抗几何变换攻击,故转而测试其对由几何校正带来的截断误差的鲁棒性;目前已有很多工作是通过估计几何变换参数来进行几何校正的[12-13].实验中,先将含水印图像进行前向几何变换,然后通过逆变换进行校正,从而得到测试图像集.这里主要考虑的几何变换是旋转和缩放.

表3 各算法针对图3(a)提取的彩色水印及其NC值

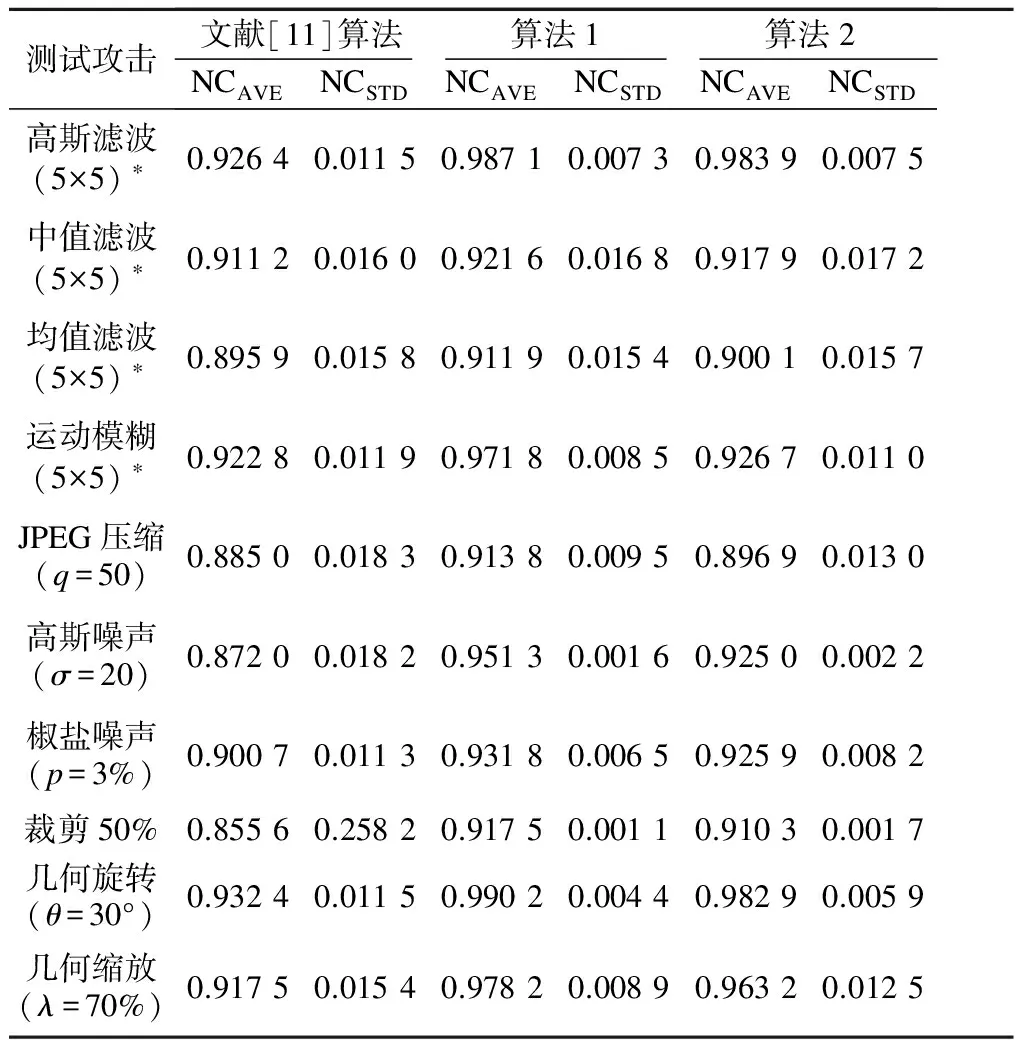
表4 各算法针对测试载体图像集的结果

由表3和表4可以看出,算法1和算法2较文献[11]算法具有更强的鲁棒性,提取水印图像质量更高,这归功于四元数彩色图像表示方法处理彩色图像的整体性.算法1的性能优于算法2,这是因为前者将水印嵌入到所有4个分量中,而后者只嵌入到1个分量中.对于裁剪攻击,由于采用了冗余嵌入策略和Arnold置乱变换,基于算法1和算法2所提取的水印都能较好识别.算法1和算法2都具有很小的NCSTD值,是比较稳定的算法.

4 结语

基于四元数彩色图像表示方法和四元数代数理论,将传统的MCLT变换推广应用于彩色图像处理中,并通过分析为避免水印能量损失问题需要注意的系数对称条件,基于MQLT变换、Arnold变换和冗余嵌入策略,提出了一种鲁棒的双彩色图像盲水印算法.实验结果表明,所提算法明显优于采用传统三通道分别处理思想的MCLT算法,针对滤波、JPEG压缩、添加噪声和裁剪等攻击具有更强的鲁棒性.这主要是因为四元数彩色图像表示方法将一幅彩色图像视为一个整体进行处理,并且考虑了色彩之间的关联性.特别是对于算法1,它充分利用四维MQLT频域,将水印嵌入到频域系数的全部4个分量中.

)

[1] Hamilton W R.Elementsofquaternions[M]. London: Longmans Green, 1866.

[2] Ell T A, Sangwine S J. Hypercomplex Fourier transforms of color images [J].IEEETransactionsonImageProcessing, 2007,16(1): 22-35.

[3] Chan W L, Choi H, Baraniuk G. Directional hypercomplex wavelets for multidimensional signal analysis and processing[C]//Proceedingsof2004IEEEInternationalConferenceonAcoustics,SpeechandSignalprocessing(ICASSP2004). Montreal, Canada, 2004: 996-999.

[4] Subakan O N, Vemuri B C. A quaternion framework for color image smoothing and segmentation[J].InternationalJournalofComputerVision, 2011,91(3): 233-250.

[5] Guo L, Dai M, Zhu M. Multifocus color image fusion based on quaternion curvelet transform[J].OpticsExpress, 2012,20(17): 18846-18860.

[6] Chen B J, Shu H Z, Zhang H, et al. Quaternion Zernike moments and their invariants for color image analysis and object recognition[J].SignalProcessing, 2012,92(2): 308-318.

[7] Malvar H. A modulated complex lapped transform and its applications to audio processing[C]//Proceedingsof1999IEEEInternationalConferenceonAcoustics,Speech,andSignalProcessing. Phoenix, Arizona, USA, 1999: 1421-1424.

[8] 陈敬昌, 胡瑞敏, 艾浩军, 等. 基于DCT-Ⅱ的MCLT快速算法[J]. 信号处理, 2005, 21(1): 63-65.

Chen Jingchang, Hu Ruimin, Ai Haojun, et al. DCT-Ⅱ based fast algorithm for MCLT[J].SignalProcessing, 2005,21(1): 63-65. (in Chinese)

[9] Shu H Z, Wu J S, Senhadji L, et al. New fast algorithm for modulated complex lapped transform with sine windowing function[J].IEEESignalProcessingLetters, 2009,16(2): 93-96.

[10] Kundur D, Hatzinakos D. Digital watermarking for telltale tamper proofing and authentication [J].ProceedingsoftheIEEE, 1999,87(7): 1167-1180.

[11] Zhang Y, Shu H Z. Digital watermarking algorithm using two dimensions modulated complex lapped transform[C]//Proceedingsof2009IEEEInternationalConferenceonDigitalImageProcessing. Bangkok, Thailand, 2009: 309-313.

[12] Zhang Y N, Wen C Y, Zhang Y, et al. On the choice of consistent canonical form during moment normalization [J].PatternRecognitionLetters, 2003,24(16): 3205-3215.

[13] Zhang H, Shu H Z, Coatrieux G, et al. Affine Legendre moment invariants for image watermarking robust to geometric distortions [J].IEEETransactionsonImageProcessing, 2011,20(8): 2189-2199.