多重网格法求解雷诺方程

许胜丽，樊文欣

（中北大学 机械工程与自动化学院，山西 太原 030051）

0 引言

内燃机的主轴承、连杆轴承承受着非常高的非稳定载荷，即动载荷，故内燃机轴承是典型动载滑动轴承。内燃机轴承在结构设计方面有很多特殊性，随着对轴承润滑理论及设计计算法研究的深入，尤其是计算机技术的发展和普及，使内燃机的设计计算方法更加完善、更加可靠、更加系统。1986 年，Osborne Reynolds在一定假设条件下，由流体力学原理提出动压滑动轴承的润滑基本方程，总结出流体膜建立动压力的机理，为流体力学润滑理论奠定基础。内燃机轴承油膜压力计算、轴心轨迹计算、最小油膜厚度计算都是以雷诺方程为基础的。

对于Reynolds方程的求解，现在主要的数值计算方法包括有限差分法和有限元法。有限差分法主要针对常用的轴承形式；有限元法用在轴瓦表面结构复杂的情况，例如开有小孔、沟槽、台阶等时。对于普通常用的轴承，采用有限差分法在很短的计算时间内就能得到比较满意的结果。有限差分法使用的是单纯的超松弛迭代法求解雷诺方程，而多重网格法是加速后的超松弛迭代方法，它比单纯的超松弛迭代法具有更短的计算时间、更高的计算精度和更快的收敛速度。本文主要研究用多重网格法求解雷诺方程。

1 多重网格法

多重网格法的实质就是求解线性方程组的一种加速收敛的手段。多重网格法的三大基本思想是：①细网格松弛，负责消除高频振荡的误差；②粗网格校正，负责低频光滑误差；③套迭代技术，负责通过限制和延拓算子连接所有层共同求解同一个问题。多重网格法就是在不同的层上进行求解，所有层相互协调地求解同一个问题，从而使高、低频偏差分量都能很快地消除和最大限度地提高迭代效率。由于限制和拖延的次数不同，多重网格法可分为如图1所示的几种循环方法。

图1 多重网格的不同循环方法

下面以两重网格“V”循环为例介绍多重网格法的计算方法。取粗网格和细网格步长，且粗网格步长是细网格步长的2倍。具体步骤如下：①设定初始值；②计算细网格上的亏损量；③从细网格到粗网格转移亏损量；④在粗网格上精确求解修正量；⑤由粗网格到细网格转移修正量；⑥计算细网格修正后的量。多次重复步骤①～⑥，直至结果收敛。

2 求解二维雷诺方程加速性验证

本文通过具体实例，验证多重网格法是一种高效的加速收敛的手段。实例是基于有限差分法求解滑动轴承的雷诺方程得到油膜压力，分别采用单纯的超松弛迭代法和多重网格法，最后再与使用了迭代精度要求的计算结果进行对比。

计算参数如下：径向滑动轴承的内径D ＝120mm，宽径比B／D＝1，偏心率ε＝0.6，半径间隙c＝0.145 5mm，轴颈转速n＝500r／min，润滑油在工作状态下的动力黏度η＝0.028Pa·s，相对间隙ψ＝0.001 1；网格密度取20×20；总迭代次数为20次。超松弛迭代法的计算过程稳定，所以第一种计算过程和多重网格法的各层计算都采用了超松弛迭代法，且取松弛因子为1.3。油膜压力的坐标原点放在轴承宽度中央。

（1）以单纯的超松弛迭代法求解雷诺方程，迭代20次，得到轴承宽度中央的周向油膜压力，如图2所示。

图2 单纯超松弛迭代法

（2）以多重网格法求解雷诺方程，得到轴承宽度中央的周向油膜压力。计算过程是采用两重网格“V”循环法，设定第一重网格迭代8＋8次，第二重网格迭代4次，即在第一重细网格上迭代8次，转移到第二重粗网格迭代4次，再转回到第一重细网格迭代8次，总共迭代20次。

第一重网格迭代8次结果如图3所示，第二重网格迭代4次，迭代次数k的值依次取1、2、3、4，且油膜压力p的初值采用第一重网格的计算结果和误差乘以相应的完全加权限制操作数。第二重网格结点（除了网格边界点）均由第一重网格的8个点包围，故设定限制操作数由第一重的每个点的1／8相加得到。应用限制操作数可把第一重的计算结果转移作为第二重计算的初值。

有了第二重网格求解结果，再转回第一重网格迭代8次，油膜压力p 的初值采取由第二重网格的计算结果乘以对应的延拓操作数得到。同样限制操作数可把第二重网格的计算结果转移作为第二次在第一重网格计算的初值。最终求解结果如图4所示。

（3）采用迭代精度要求为0.01的相对误差来限制迭代次数，得到轴承宽度中央的周向油膜压力。此次计算比前面两种计算在精度上要高，用时也长，更接近精确值，所以它可以作为前面两种计算方法相对比的标准。

增加收敛准则，用迭代精度要求来限制迭代结果，保证相对误差为0.01，求解结果如图5所示。

由图2、图4和图5可知，将迭代同样的次数分别用单纯的超松弛迭代法和用多重网格法求得的结果与使用迭代精度要求0.01相对误差的结果比较，可知多重网格法的迭代结果更接近精确值，说明多重网格法有更高的迭代效率。在一般求解径向滑动轴承的雷诺方程时，都要求达到一定精度，采用普通的计算方法，可能要迭代的次数非常多，同时也非常耗时；而用多重网格法能在很少次数的迭代中达到很高的迭代精度，减少了计算量、节省了计算时间。

图4 第三层网格求解结果

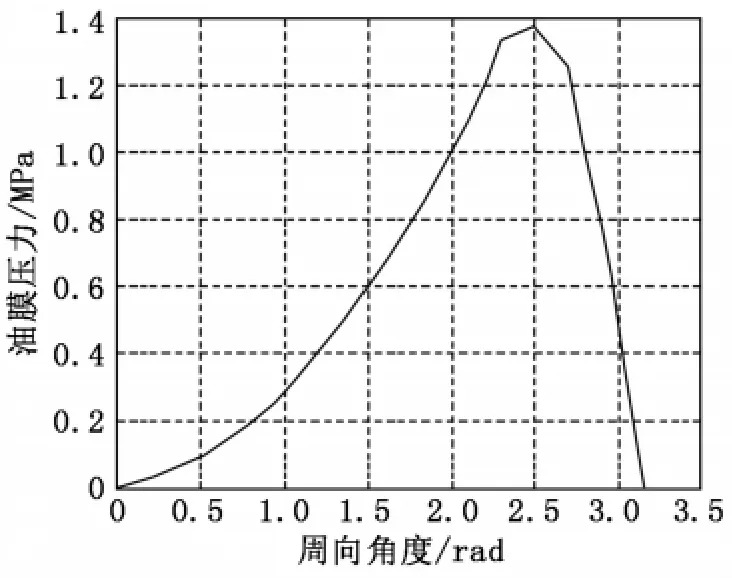
图5 相对误差为0.01的迭代结果

3 结束语

在求解二维雷诺方程中，使用常规的单网格，如果要达到很高的精度，将需要迭代相当多的次数，整个计算过程也将耗费很多时间，但是采用多重网格法在各层网格上进行较少的迭代，便可以得到接近精确解的解，所以多重网格法求解雷诺方程将可以比较快地达到所要求的精度，是一种比较高效的计算方法。

［1］ 谢帆，荆建平，万召，等.基于有限差分法的径向滑动轴承油膜压力分布计算［J］.润滑与密封，2012，37（2）：12－15.

［2］ 敏政，王乐，魏志国，等.基于MATLAB 技术的滑动轴承油膜压力分布的模拟［J］.润滑与密封，2008，33（8）：51－53.

［3］ 王伟，张祖立.基于Matlab有限长液体动压滑动轴承压力分布的一种近似解法［J］.沈阳农业大学学报，2005，36（2）：247－249.

［4］ 张直明.滑动轴承的流体动力润滑理论［M］.北京：高等教育出版社，1986.

［5］ 孟繁娟，杜永平.径向滑动轴承油膜压力分析［J］.轴承，2008（1）：23－25，32.

［6］ 戴惠良，刘思仁，张亮.滑动轴承油膜压力的新算法［J］.机床与液压，2011，39（11）：27－28，64.