基于ADAMS与MATLAB的电磁制动器仿真分析

宋小龙，李 枝，王文清，杨 瑞

（宝钛集团有限公司 宽厚板材料公司，陕西 宝鸡 721014）

1 ADAMS技术简介

ADAMS软件是美国MDI公司开发的机械系统动力学仿真分析软件，它使用交互式的图形环境和零件库、约束库、力库，创建完全参数化的机械系统几何模型，其求解器采用多刚体系统动力学理论中的拉格朗日方程方法，建立系统动力学方程，对虚拟机械系统进行静力学、运动学和动力学分析，输出位移、速度、加速度和反作用力曲线。

ADAMS主模块见图1。ADAMS／View 建模仿真步骤见图2。

图1 ADAMS主模块

2 双块式电磁制动器的建模仿真

2.1 系统描述

本文所用的模型为双块式电磁制动器，其动力学简化模型如图3所示，它由位于制动轮A 两旁的两个制动臂D1、D2和两个闸瓦B1、B2组成。其工作原理如下：由弹簧通过制动臂及闸瓦使制动轮经常处于制动状态，当松闸器C通入电流时，利用电磁力作用，通过推杆使制动器两边的闸瓦松开。

2.2 ADAMS模型

在ADAMS中建立的仿真模型见图4。

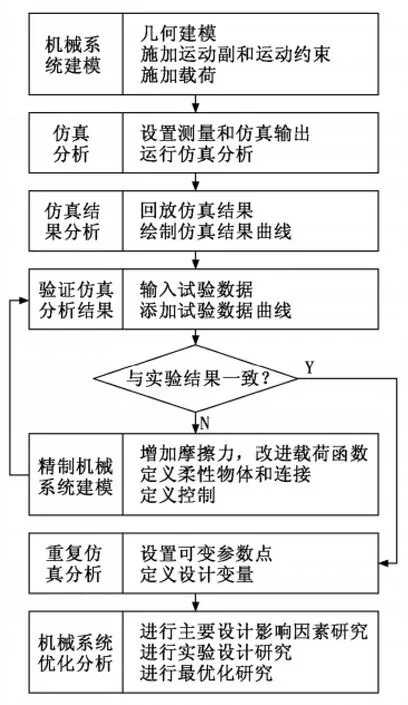
图2 ADAMS／View 建模仿真步骤

2.3 动力学仿真

仿真初始条件如下：松闸器C 通入电流时，利用电磁力作用，通过推杆使制动器两边的闸瓦松开，制动轮A 以3 000°／s的角速度开始转动，经过0.1s后，松闸器C断开电流，失去电磁力，同时，弹簧S通过制动臂及闸瓦B1、B2开始制动。

图3 电磁制动器的动力学简化模型

我们在对此模型进行模拟仿真时，输出了制动臂在横向X、纵向Y 和垂直方向Z 的加速度曲线图，本文给出的是制动臂D1的时域曲线图，见图5。

图4 ADAMS中的仿真模型

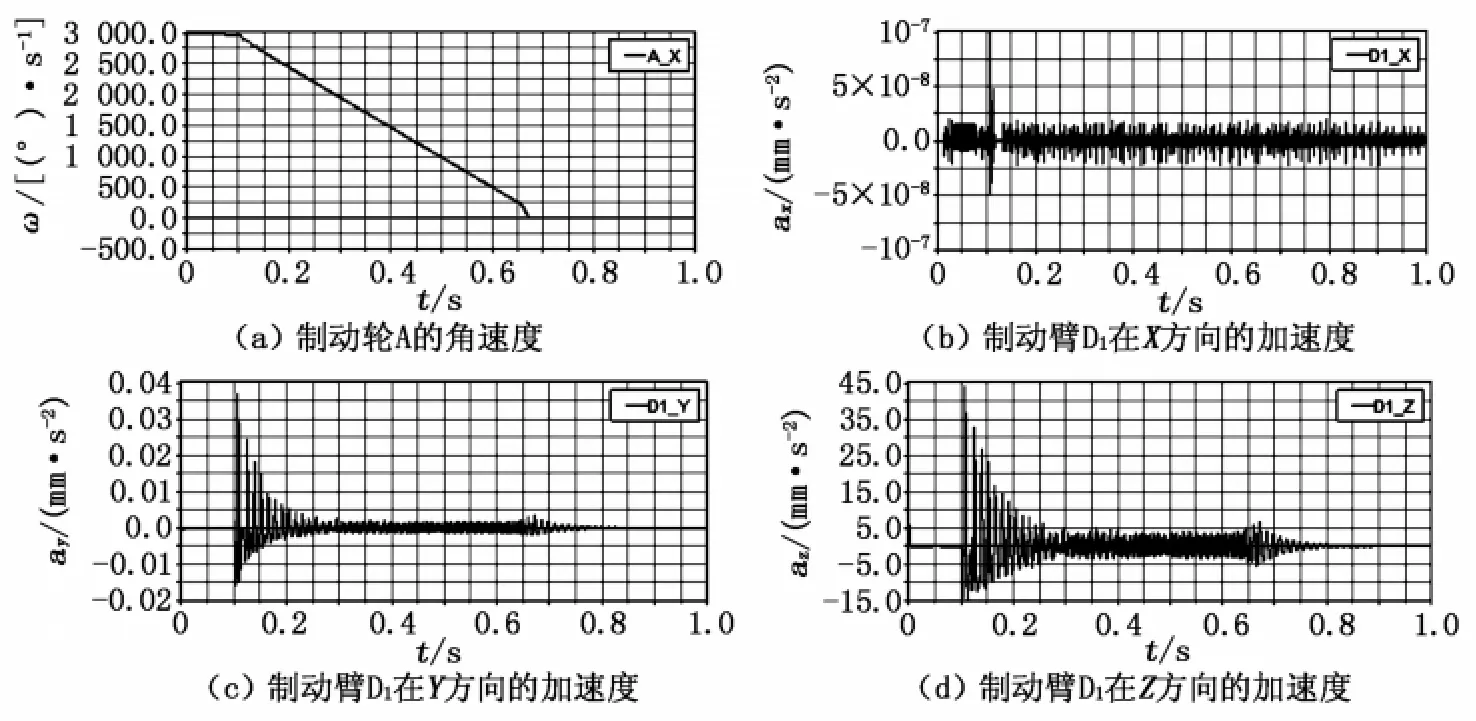
图5 制动轮的转速和制动臂各方向的加速度

从图5可以明显看出：制动臂D1在Z 方向的加速度远远大于X、Y 方向的加速度，这说明在制动过程中制动臂D1在Z 方向产生的振动幅值最大。

图6为图5（d）的频域图，从中我们可以看到大约在80Hz频率的幅值达到最大值。

3 MATLAB小波分析

本文利用MATLAB软件编程程序和小波工具箱（Wavelet Toolbox）的主要功能，对制动臂D1在Z 方向产生的加速度信号进行小波分析。

图6 制动臂D1 在Z 方向的加速度频域图

我们对制动臂D1在Z 方向的原始信号时域图进行小波变换，选用db小波，进行4层分解，尺度取整数1～1 000，如图7所示。图7中，T 表示时间，由于原始信号时间段为1s，此处小波变换三维图中的时间值2 000就相当于1s。

从图7（a）、7（b）可以看到，在低时间段的低频处小波积分幅值较大，在0.2s以后幅值逐渐减小，在高时间段的高频处小波积分幅值接近于零。

图7 制动臂D1 在Z 方向的原始信号连续小波变换

用小波分析此振动加速度信号S，图8为冲击信号的小波分解，分解4次得到低频逼近信号a4和高频细节信号d1、d2、d3和d4，对应频带分别为d1（500Hz～1 000Hz），d2（250 Hz～500 Hz），d3（125 Hz～250 Hz），d4（62.5Hz～125Hz），a4（0Hz～62.5Hz）。原始信号S 的离散小波变换分解可表示为：

S＝d1＋d2＋d3＋d4＋a4。

各分解信号的横坐标均为时间，等于原信号的时间历程。从图8中可以看出在频段d4（62.5 Hz～125 Hz）上的信号明显偏离振动中心线，从而导致了总振动信号的非对称性分布。

图8 制动臂D1 在Z 方向的冲击信号小波分析4层分解

接下来对原信号进行降噪处理，降噪后进一步产生了残差信号的时域图和频谱图，见图9。

图9 制动臂D1 在Z 方向的小波降噪图和残差信号图

从图9（b）中可以看出，此振动信号的故障频率大约在80Hz左右，这与先前仿真产生的制动臂D1在Z方向的加速度频域图的最大幅值正好相吻合，并且这个频率也正处于高频细节信号频段d4（62.5Hz～125 Hz）中。

通过ADAMS 和 MATLAB 联合仿真说明，MATLAB小波残差信号处理方法能有效地提取ADAMS中仿真故障信号的特征频率，是一种良好的信号处理方法。

4 结论

经过以上分析可以看出，利用ADAMS和MATLAB两个强大的软件工具进行联合仿真分析，不仅能够提高工作效率，缩短工作周期，而且还可以通过获取的各种图形，准确快速地预测分析设备在运行中的故障问题，达到良好效果。

［1］ 郑建荣.ADAMS虚拟样机技术入门与提高［M］.北京：机械工业出版社，2001.

［2］ 陈立平.机械系统动力学分析及ADAMS应用教程［M］.北京：清华大学出版社，2005.

［3］ 何正嘉.机械设备非平稳信号的故障诊断原理及应用［M］.北京：高等教育出版社，2000.

［4］ 飞思科技产品研究开发中心.小波分析理论与MATLAB7实现［M］.北京：电子工业出版社，2005.

［5］ Liu B.Selection of wavelet packet basis for rotating machinery fault diagnosis［J］.Journal of Sound and Vibration，2005，284：567－582.

［6］ Cheng Junsheng，Yu Dejie，Yang Yu.Application of an impulse response wavelet to fault diagnosis of rolling bearings［J］.Mechanical Systems and Signal Processing，2007，21：920－929.