码垛机械手结构轻量化设计

李占贤，李兆盈

（河北联合大学 机械工程学院，河北 唐山 063009）

1 码垛机械手轻量化设计方案

本文开发的用于陶瓷坐便器装卸车的码垛机械手为直角坐标结构，具有4个自由度，如图1所示。横行基座通过导轨滑块沿X 向运动，走行横梁通过导轨滑块在支撑梁上沿Y 向运动，提升臂沿Z 向运动，叉子做旋转运动。机械手整体采用结构钢，跨度为7 m×5m，高3m，空载运行速度为35m／min，重载运行速度为25m／min，其跨度大、速度高、运动质量大。

图1 码垛机械手直角坐标结构

采用有限元分析软件对机械手结构进行分析：

（1）建立装卸机械手各关键零件的三维几何模型及整体几何模型，在不影响计算结果的前提下，对模型做适当的简化处理。

（2）建立有限元计算模型，包括选定单元类型、划分网格、确定边界条件、施加约束及载荷等。

（3）分析机械手在静态工作情况下的受力分布及变形情况，对局部结构进行优化，改善机械手的受力情况。

（4）选择几种机械手的结构优化方案，并对几种方案进行对比分析，最后确定机械手的总体轻量化设计方案，在保证满足机械手结构承重能力的前提下，减轻机械手质量，有效降低机械手惯量及动态负荷，使机械手运动更灵活。

2 机械手各关键零件的轻量化设计

2.1 叉子结构的静力分析及优化

机械手叉子由方管和钢板焊接而成，结构上叉子属于悬伸件，受使用空间限制，其结构薄弱，变形应力大，因此有必要对其进行分析。利用ANSYS有限元分析软件建立叉子的有限元模型，采用Solid92 的3D10节点四面体结构实体单元对叉子进行网格划分，对叉子施加边界约束条件和载荷，叉子旋转轴承处作为支撑点限制3个方向自由度，叉子上表面处承受载荷40kg。加载及约束后进行分析计算，分析结果如图2、图3所示。

图2 叉子结构应力图

叉子最大位移发生在叉子齿最外端，为0.813mm；最大应力发生在叉子与旋转轴连接处，为166 MPa。叉子所受载荷一部分来自于自重，一部分来自于承载重物。叉子承载重物为定值，对叉子进行轻量化设计时主要考虑减轻叉子自重，而叉子的质量主要集中在叉座。提出如下改进方案：

方案一：在结构允许的情况下将叉座高度由原来的173mm 变为120mm。经分析计算叉子质量减轻了8.2%，最大应力降低了6%，但最大变形增加了9.4%。变形增大的原因在于叉座高度的变化减弱了筋板的作用。为了减小变形，可以加大筋板长度，但这样会导致叉子承载平面面积减小。为此，在方案一的基础上提出改进方案二。

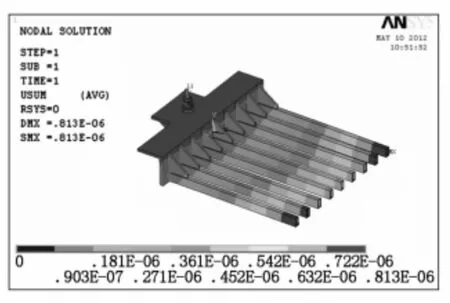
图3 叉子结构位移图

方案二：将筋板改到叉子齿下面，这样不仅可以加大筋板长度，而且筋板受力由原来的拉应力改变为压应力，改善了筋板的受力状况。叉子上表面去掉筋板后，在保持原叉子承载面积的情况下缩短叉齿长度，由原来的800mm 减小到680mm。同时，在叉座上承力不大的位置增加工艺孔以减轻重量。

各方案的三维实体模型对比如图4所示。方案二的受力情况大为改进，最大变形量减少了0.011mm，重量减轻了37.6%，空载情况下转动惯量减小了33.4%，大大提高了机械手运动的灵活性。

图4 叉子结构轻量化方案对比

2.2 提升臂结构的静力分析及优化

提升臂由槽钢和钢板焊接组成，质量很大，结构悬伸大，原设计导轨位于提升臂后面，齿条位于提升臂左侧面。将提升臂与优化后的叉子连接在一起进行分析，划分网格后对提升臂齿条的齿面施加3个方向自由度约束，叉子上表面处承受载荷40kg，加载及约束后进行分析计算。分析结果如图5～图8所示。

为了提高提升臂的灵活性，减轻质量，做如下改进：

方案一：将原设计中的槽钢改为双侧钢板。原设计中双导轨位于提升臂后面，由于结构空间所限将双导轨改在右侧面。

方案二：导轨分别在两个侧面对称布置。

叉子在工作时会在180°的范围内旋转，不同位置时受力状况不同，选取叉子两种特殊位置进行受力分析，分析结果见表1。提升臂最大位移发生在叉子齿最外端，提升臂最大应力发生在叉子与旋转轴连接处。

图5 叉子位于正面时提升臂应力图

图6 叉子位于正面时提升臂位移图

图7 叉子位于右侧面时提升臂应力图

图8 叉子位于右侧面时提升臂位移图

3种方案的载荷情况相同，因此3种方案的最大应力几乎相同。方案一在两个位置的最大位移相差不大，并且在质量上相对于原设计降低了20.5%，因此采用方案一实现轻量化的目的。

表1 提升臂轻量化设计方案对比

2.3 走行梁结构及横行基座结构的静力分析及优化

码垛机械手走行梁由槽钢和钢板焊接组成，为单梁结构，提升臂位于走行梁侧面，通过导轨滑块与走行梁连接，走行梁除了受到提升臂、叉子自重以及载重货物垂直向下的应力外，还受到提升臂等的扭矩作用。对走行梁采用Solid92的3D10节点四面体结构实体单元建模并划分网格，在走行梁与支撑梁导轨相连的滑块接触面处施加3个方向自由度，当提升臂连同叉子运行到中间位置时走行梁受力变形最大，因此选择此位置进行分析。

图9、图10为走行梁结构应力图和位移图。走行梁的最大应力为29.8 MPa，最大位移为0.89mm，扭转角度为0.055 2°，最大位移处为走行梁中间位置。为减少提升臂的扭转力矩作用导致的梁变形，改变走行梁结构形式，采用双梁结构，导轨采用侧面布置，如图11所示。走行梁两种方案对比见表2。

图9 走行梁结构应力图

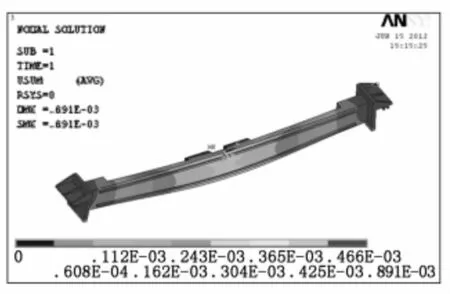
图10 走行梁结构位移图

图11 走行梁新方案——双梁结构

表2 走行梁方案对比

由表2可知：新方案最大应力和最大位移均与原方案几乎相同，扭转角度减少了43.1%，质量比原设计减轻了20.4%，大大降低了结构质量，改善了走行机构的灵活性。

3 轻量化设计结果

为了验证轻量化设计的结果，将原设计与修改后的装卸车机械手整体建模进行对比，结果如图12～图15所示。原设计方案最大变形位移为18.3mm，最大应力为134 MPa；轻量化之后最大变形位移为1.8 mm，最大应力为99.6 MPa。因此轻量化设计达到了设计目的。

图12 原设计应力图

图13 原设计位移图

图14 新方案应力图

4 结束语

本文利用ANSYS软件对机械手关键零部件建立有限元模型进行分析研究，通过分析结果来改进零部件的设计，进行多方案对比后选择合适的设计方案，达到了对机械手轻量优化设计的目的。

图15 新方案位移图

［1］ 尚晓江，邱峰，赵海峰，等.ANSYS结构有限元高级分析方法与范例应用［M］.北京：中国水利水电出版社，2005.

［2］ 曾攀.有限元分析及应用［M］.北京：清华大学出版社，2004.

［3］ Zienkiewicz O C，Talor R L.有限元方法第1卷：基本原理［M］.第5版.曾攀，译.北京：清华大学出版社，2008.