金属切削过程的有限元数值模拟

张军峰

（陕西理工学院 机械工程学院，陕西 汉中 723003）

0 引言

金属切削过程是指通过切削运动去除多余的金属层而形成切屑和已加工表面的过程，在此过程中会产生变形、温度升高、刀具磨损等诸多现象。切削过程是一个复杂的工艺过程，本文利用基本的弹塑性理论，建立材料的二维模型；采用模拟方法，对二维正交金属切削整个过程进行仿真，提取不同阶段的应力应变分布云图，分析切削区域的变化过程，为金属切削刀具优化提供更合理的依据。

1 基本理论

对于二维切削过程，弹性变形阶段服从胡克定律，关系表示为：

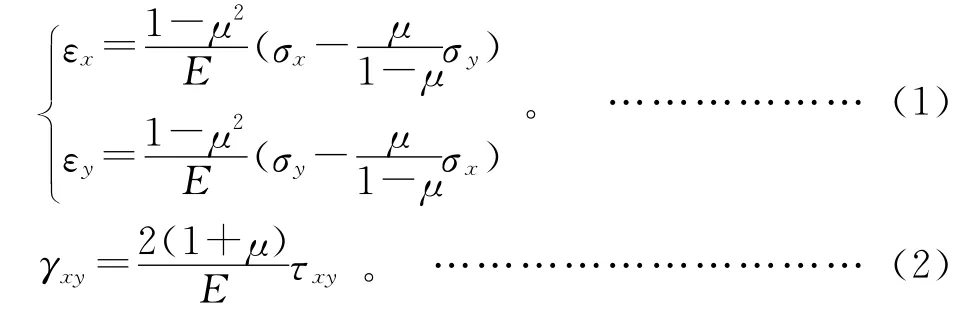
其中：εx、εy为正应变；σx、σy为正应力；τxy为剪应力；γxy为剪应变；E 为弹性模量；μ 为泊松比。

当应力之间服从Von Mises屈服准则时，材料处于塑性状态，其表达式为：

其中：J2为应力偏张量的第二不变量；C 为常量。

将J2用3个主应力σ1、σ2、σ3合成表示为：

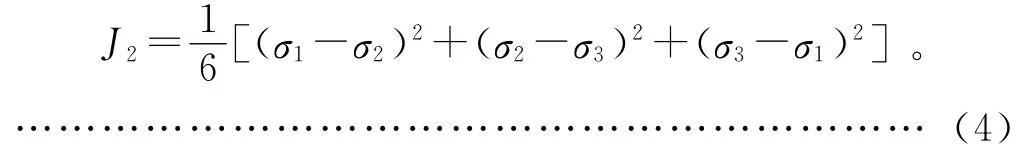
式（4）中3个主应力σ1、σ2、σ3是一元三次方程（5）的3个实根：

其中：I1＝σx＋σy＋σz；I2＝－（σxσy＋σyσz＋σzσx）＋τxy2＋τyz2＋τzx2；I3＝σxσyσz＋2τxyτyzτxz－σxτyz2－σyτxz2－σzτxy2。

2 有限元模型的建立

金属切削中，刀具材料比工件硬，模型建立时，刀具确定为刚体，工件确定为柔体，选择大应变弹塑性单元Visco106模拟工件、Plane182模拟刀具进行分析。设刀具前角为10°，后角为6°；工件模型长度为25mm，高度为15mm；刀尖半径为零，认为绝对锋利；切削厚度为5mm，切削速度为100mm／min。

2.1 建立材料模型

工件选择45 钢，弹性模量E＝200GPa，泊松比μ＝0.28，屈服强度σs＝355 MPa，强度极限σb＝610 MPa，极限变形δ＝0.18。刀具选择YT5类硬质合金，弹性模量E＝600GPa，泊松比μ＝0.3，摩擦系数为0.3。选择ANSYS软件建立有限元模型，采用映射法划分网格，工件分割成2 015个单元，刀具分割成110个单元。工件底部限制X 向 和Y 向，左侧限制X 向；刀具限制Y向。二维直角切削的有限元模型如图1所示。

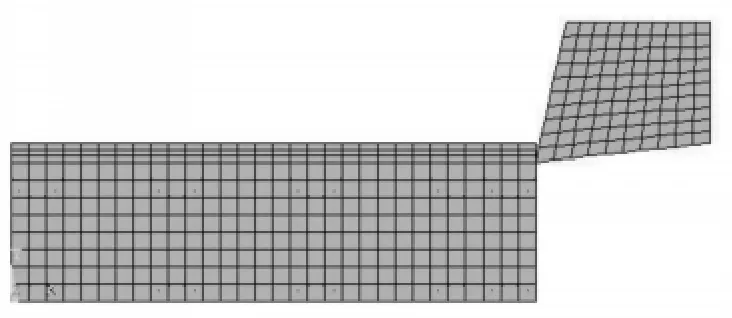
图1 二维直角切削的有限元模型

2.2 定义节点耦合

由于节点自动分离不能实现，因此首先判定切屑层和移动路径，并沿着切削路径方向建立已加工表面和切屑底层的初始联系，即利用映射法划分网格时，使已加工表面与切屑底层单元长度和数目相等，并在每一对重合的节点上建立全耦合。

2.3 定义接触

由于刀具比工件硬，因此模型建立时，刀具是弹性体，工件是弹塑性体，二者之间的接触确定为刚体对柔体的接触，完全符合实际切削过程。

切削过程中，刀具后刀面与已加工表面之间、刀具前刀面与切屑底层之间的接触，都定义为面对面接触。刚体面被当作“目标”面，用Targe169来模拟；柔体面被当作“接触”面，分别选用Conta171和Conta172来模拟。所以，金属切削中存在两个接触对，即后刀面与已加工表面和前刀面与切屑底层的接触。

2.4 切屑分离

工件材料撕裂形成切屑就是节点的连续分离，目前采用的分离标准有几何标准和物理标准两类。选择物理标准更符合实际情况，因此采用等效塑性应变的分离标准并设定分离的等效应变值为0.8。

2.5 添加约束及载荷

工件施加位移全约束，左侧约束X 向位移；刀具约束Y 向位移，刀具运动方向为水平向左，对右侧边界施加X 向微小位移载荷。添加约束及载荷后的模型见图2。刀具切削过程分多步骤进行，每计算一次保存一次结果，并继续重复添加新的位移载荷，反复计算。

图2 添加约束及载荷

3 计算结果及分析

3.1 应力场分析

图3为刀具前进不同位移时的等效应力云图。图3（a）为工件最大等效应力带，该应力带顺着切削方向在切削层内流动，并位于剪切层。这说明，到达第一变形区后发生塑性变形，等效应力达到最大值；此后，随着温度的升高，变形增大，但应力值却减小，体现出材料的不稳定性。图3（b）、图3（c）表示在不同的切削阶段，最大等效应力随着位置和面积不断变化，但其值是个常量。这就验证了Von Mises屈服准则：当材料进入塑性状态时，等效应力保持不变。

图3 刀具前进不同位移时的等效应力

后刀面的等效应力值均比前刀面大，且最大值位于刀尖点及后刀面靠近刀尖区域，说明后刀面受到的挤压和摩擦较大，后刀面更易磨损。

3.2 应变场分析

图4为刀具前进不同位移时的塑性等效应变。由图4可以看出，开始碰刀时，产生等效塑性应变，沿着切入方向等效塑性应变向切屑层扩展，方向是和切削速度方向成剪切角，形成一等效塑性应变层，即剪切层。

图4 刀具前进不同位移时的塑性等效应变

4 结论

本文利用有限元软件模拟二维直角切削过程，分析切削区应力应变变化的过程。在后续的研究里，可将二维直角切削扩展为三维斜角切削，与实际加工过程更加符合，实现刀具几何参数的优化，以利于更好地将研究成果用于工程问题的分析中。

［1］ 陈志刚，周里群，黄霞春.基于ANSYS的金属切削过程有限元仿真［J］.凿岩机械气动工具，2007（1）：46－54.

［2］ 郭丹.高速铣削中基于正交切削模型的有限元模拟［D］.苏州：苏州大学，2008：29－31.

［3］ 陈志刚.金属切削过程及内圆磨削过程有限元仿真［D］.湘潭：湘潭大学，2007：20－26.

［4］ 谢峰，赵吉文，刘正士，等.二维金属切削过程的数值模拟［J］.系统仿真学报，2004，16（7）：1412－1417.

［5］ 宋凯磊.废旧线缆资源化破碎设备研究［D］.天津：天津大学，2009：28－38.

［6］ 张焕.电沉积镍涂层钢板的界面强度和成形性能分析［D］.湘潭：湘潭大学，2009：35－40.

［7］ 王丽平，王秀伦，马自勤.金属切削过程的有限元模拟［J］.工具技术，2009，43（4）：59－61.