航天器运输包装箱悬置系统仿真分析

白峭峰，梁海龙，梅小龙，刘国志

（1.中北大学 机械工程与自动化学院，山西 太原 030051；2.山西北方机械制造有限责任公司 火炮研究所，山西 太原 030009）

0 引言

运输过程中，运输车辆发动机的振动、路面高低不平激励引起的冲击，以及其他各种原因带来的振动，都会使航天器包装箱内的零件所受载荷增加，可靠度降低，影响其性能和精度。因此，为了减少振动和冲击的危害，需要有效地隔振缓冲，尽量把运输过程中的机械振动带来的损害降到最低，保持航天器的优良品质。

从隔振的角度来考虑，悬置装置是越软越好，这样传递出来的振动才最小，但从支撑和限位的角度来考虑，悬置装置是越硬越好，这样才能保证空间结构的紧凑性。很明显这两者是互相矛盾的，因此在实际使用过程中，应该找到一个折中的方案使其能较好地满足两个方面的要求。

1 隔振系统的动力学建模

航天器包装箱隔振系统所用的隔振元件在运输设备上安装时一端固定在包装箱上，另一端固定在与运输设备刚性连接的支架上。悬置隔振元件在三维方向上都有弹性，但由于发动机的各支承点相距较近，故常略去其扭转弹性，而将其简化为分别沿其3个弹性主轴的三弹簧阻尼元件。

航天器包装箱隔振系统的弹性振动系统固有频率不超过30Hz，包装箱及航天器的质量和刚度一般比隔振器大得多，且前者的固有频率远高于路面激励频率，故将包装箱及航天器组视为刚体。这样，包装箱隔振系统物理学模型即为空间6 自由度的弹性振动系统，其动力学6自由度模型如图1所示。

包装箱系统6自由度运动微分方程为：

其中：M 为系统的惯性矩阵；C 为系统的阻尼矩阵；K为系统的刚度矩阵；Q 为广义力；q为系统的变形量。

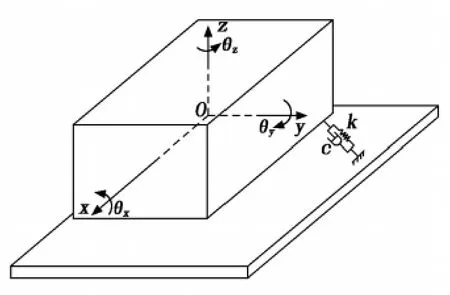
图1 航天器包装箱隔振系统物理模型

2 系统振动的动能及惯性矩阵

包装箱系统振动的动能T 包含系统随质心平动时的平动动能T平和绕质心转动时的转动动能T转两部分，即：

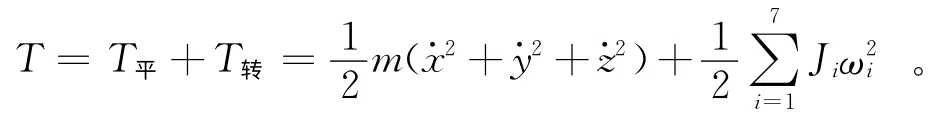
其中：Ji为系统中第i个部件的转动惯量；ωi为第i 个部件的质心相对于系统质心转动的速度。

在微小振动的假设下，系统动能用角位移和角速度矢量可表示为：

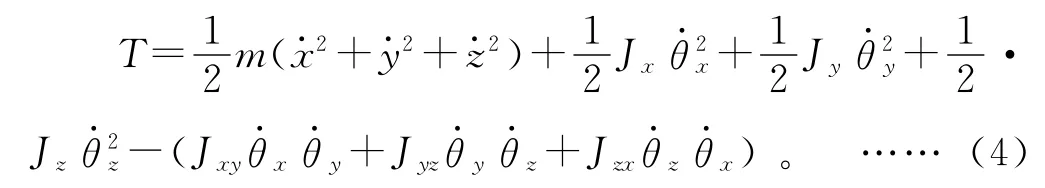
其中：Jx、Jy、Jz分别为动力总成绕对应下标轴的转动惯量；Jxy、Jyz、Jzx分别为动力总成绕对应下标平面的惯性积。

将式（4）写成矩阵形式为：

3 系统振动的势能及刚度矩阵

设系统静平衡位置为零势能点，不计发动机总成重量势能的变化，则包装箱系统支承元件由于弹性变形而产生的势能即为振动势能。悬置系统的势能为：

其中：kui、kvi、kwi分别为对应于3 根弹性主轴的主刚度；Δui、Δvi、Δwi分别为第i 个悬置在其弹性主轴上引起的微量变形；ΔSi＝［Δui，Δvi，Δwi］T。

将悬置元件的3根弹性主轴ui、vi、wi与物理oxyz的变换关系代入式（6）得：

4 系统振动的耗散能及阻尼矩阵

悬置系统的耗散能为：

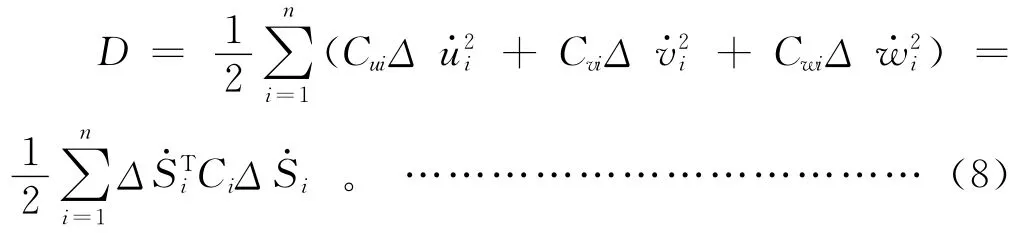
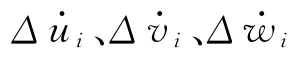
将悬置元件的3根弹性主轴与物理o－xyz 的变换关系代入式（8）得：

5 系统状态方程

将所求得的M、C 代入系统状态微分方程得：

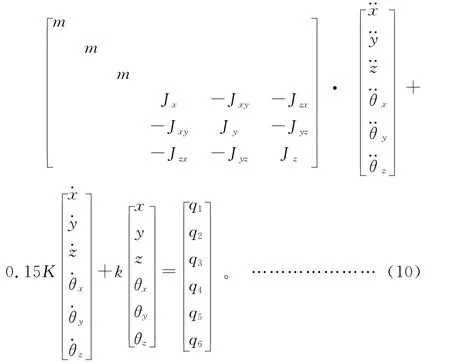
6 Simulink模型的建立

本课题的系统很复杂，创建Simulink模型变得很庞大而且难于读懂。在这里利用Simulink的子系统可使模型创建变得简捷、易懂易用。根据系统的状态方程式可建立如图2所示的Simulink模型。

在图2中利用了6个子系统，每个子系统对应一个自由度的数学方程。

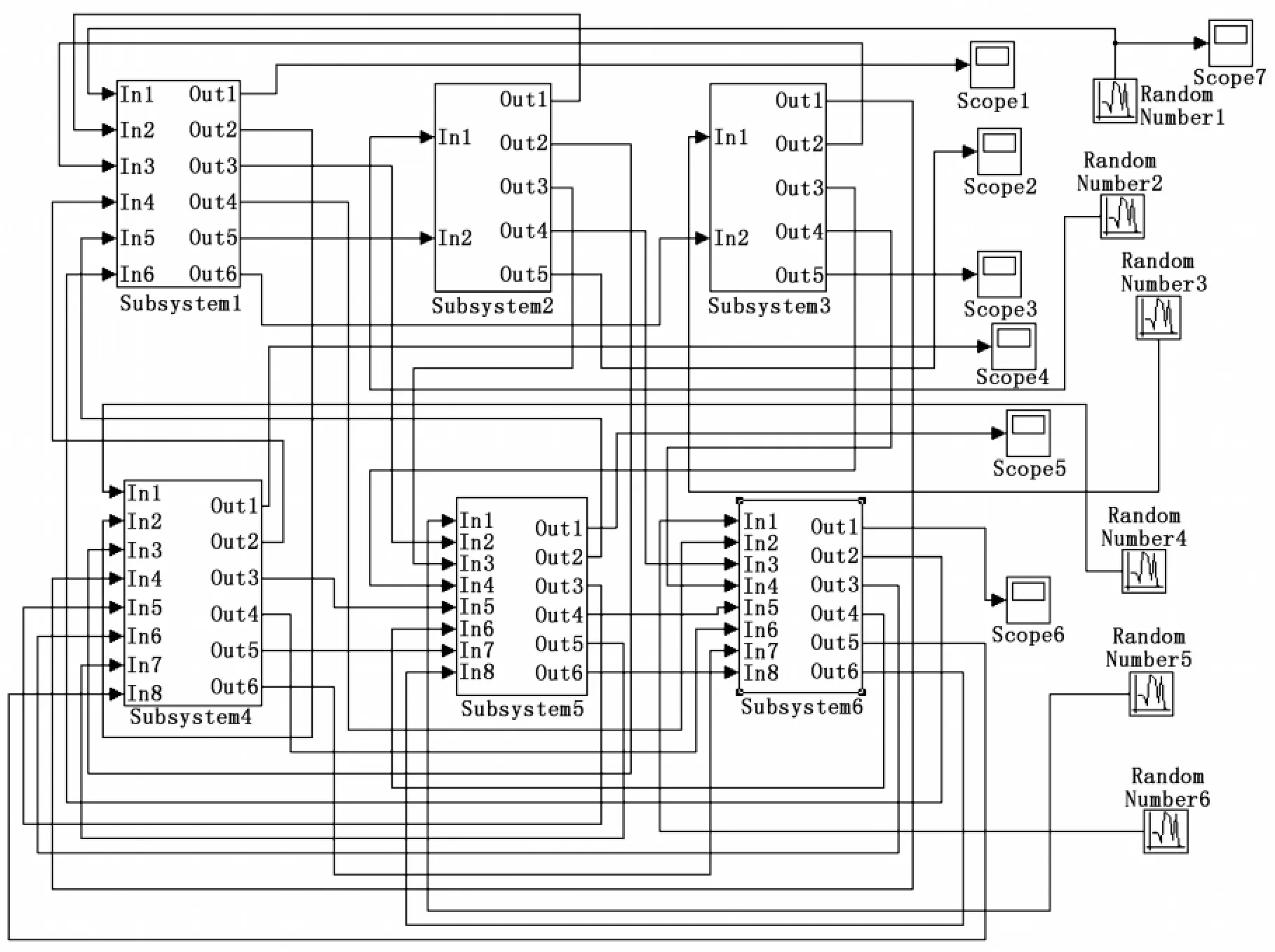
图2 系统Simulink模型图

7 小结

本文主要利用振动理论对悬置系统进行了理论分析，结合对包装箱悬置系统的减振要求，从能量平衡的原理出发建立了悬置系统的受迫振动微分方程，并对该方程进行了理论分析和数值求解，最后利用MATLAB／Simulink建立模型进行仿真。

［1］ 朱石坚，楼京俊，何其伟.振动原理与隔振技术［M］.北京：国防工业出版社，2006.

［2］ 徐登峰.超精密系统中主被动隔振技术的应用及隔振性能测试分析［J］.制造技术与机床，2007（1）：109－111.

［3］ 黄鼎友，吉向东.动力总成悬置系统建模及振动仿真［J］.江苏大学学报，2005，26（3）：221－226.

［4］ 王沫然.Simulink4建模及动态仿真［M］.北京：电子工业出版社，2001.