含特殊管段的含蜡原油管道热力计算与分析

林名桢

（胜利油田胜利勘察设计研究院有限公司工艺配管所，山东东营257026）

对于含蜡原油，传统的输送方式是采用逐站加热的方法，热油管道的输油温度一般高于凝点，但管道停输时间过长仍可导致凝管。近年来因各种原因导致管道的停输日益频繁，故开展热油管道停输再启动特性的研究具有十分重要的工程意义。迄今为止，虽然人们在这一方面的研究取得了较大的成就［1－2］，但这些研究一般都是在固定管道直径和管外环境的基础上进行的，很少考虑管内外情况的变化问题。实际上长输管道沿线常常会出现架空或浸没在水中的管段，此外，管道内某些位置也经常会形成一定的结蜡层［3－4］。这些特殊管段对管道的热力特性有重要影响。基于此，笔者对含特殊管段的含蜡原油管道在不同工况下的热力特性进行了详细的计算分析。

1 数学模型

1.1 管道正常运行过程中的数学模型

在管道正常运行中一般认为其温度场均处于准稳定状态，并假定管道同一截面上的油流温度相同。其中油流温度计算公式以及管外介质热传导方程［5－6］分别见式（1）、（2）。

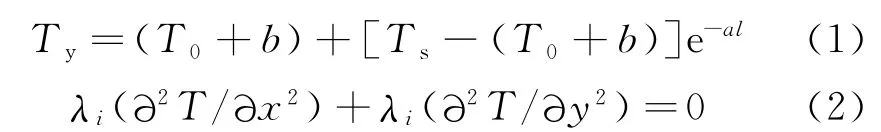
其中，Ts、Ty分别为计算管段起点和终点油温，℃；a＝KπD／（Gc），b＝giG／（KπD）；l为计算段长度，m；G 为油品质量流量，kg／s；c 为计算段原油比热容，J／（kg·℃）；D 为计算直径，m；K 为计算管段总传热系数，W／（m2·℃）；T0为管道埋深处土壤自然温度，℃；i为油流水力坡降；g 为重力加速度，m／s2。

1.2 管道停输过程中的数学模型

为了计算方便，一般将管道停输过程中的数学模型简化成如下形式［7］：

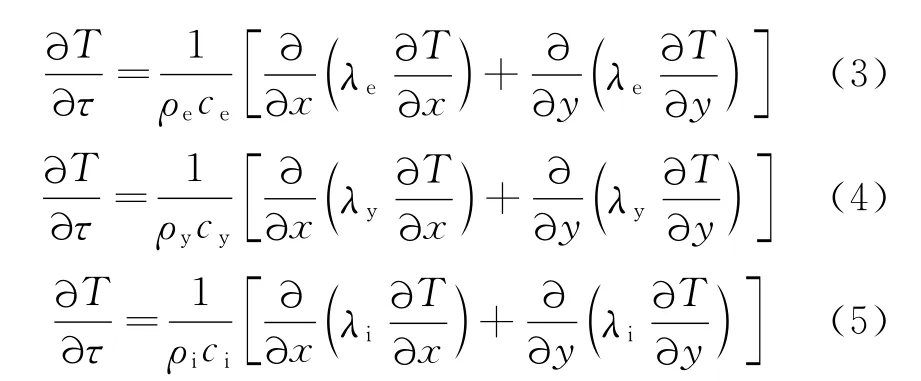
其中，ρe、ρy分别为凝油、液态油的密度，kg／m3；λe为液态油当量导热系数，W／（m·℃）；ρi 分别为结蜡层及其它介质的密度；kg／m3；ce，cy分别为凝油、液态油的比热容，J／（kg·℃）；ci分别为结蜡层及其它介质的比热容，J／（kg·℃）。

1.3 热油管道再启动过程中的数学模型

热油管道的再启动过程实际上是热力水力相互耦合的过程，管道内油流的热力水力耦合模型［7－9］如下，而管外介质的传热模型与停输过程相同。

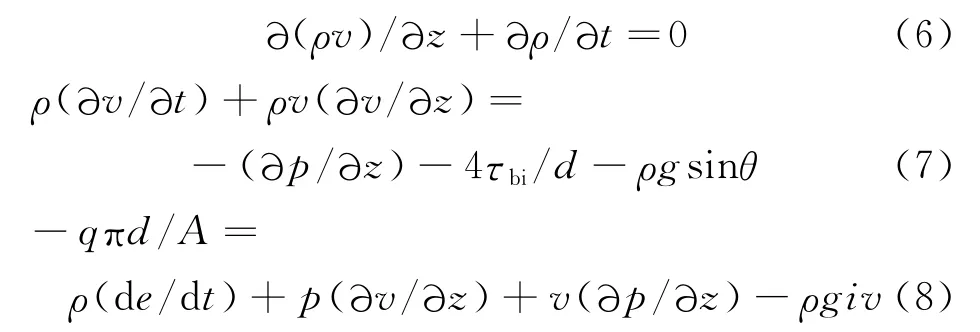
其中，v 为流速，m／s；ρ 为液体密度，kg／m3；e 为单位质量流体的总能量，J／kg；A 为油流面积，m2；θ为管轴与水平线的夹角，（°）；q 为热流密度，W／m2。

1.4 边界条件

在上述三组模型中埋地段管道横截面热传导过程中的边界条件是相同的，具体情况可参看文献［6－9］。

对于架空管道和浸水管道而言，管道外壁与管外介质之间的边界条件分别为：

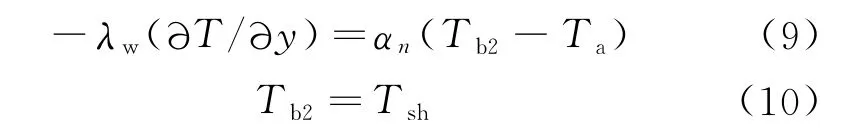
其中，Tb2为管道最外层的管壁温度，℃；Ta为管道周围空气的温度，℃；Tsh为管道周围水的温度，℃。

2 模型的求解

分别利用列宾宗公式、有限元法以及热力特征线法对处于不同工况下管道油流温度以及土壤温度场进行求解，具体方法见文献［8－9］。同时考虑了特殊段的存在，又对一些问题进行了特殊处理。

2.1 结蜡厚度的确定

以原油的析蜡点温度为界将管道分成两段进行研究。其中未结蜡管段长度可按公式（11）进行反算：

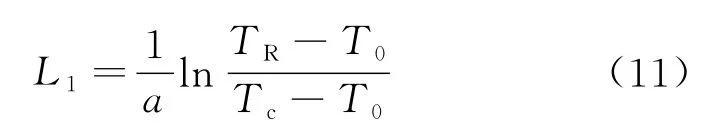
其中，TR为管道出站温度，℃；Tc为原油析蜡点温度，℃。

根据未结蜡管段的摩阻损失可计算出两端分界点的压力，进一步求出结蜡段的平均水力坡降i，然后利用公式i＝β（Q2－mvm／d5－m）来求管道的等效直径d。因β、m 值随着原油的流态而变化，而要判断流态，又离不开d，故此处要进行迭代计算。计算中将所有状态的β、m 值放在一个数组中，设置一个循环程序，逐个选取β、m 值来计算d 值，然后利用值求解雷诺数，再利用雷诺数判断流态，若流态与选取的m 值相对应，则说明计算的d 值与实际相符，终止循环，否则继续取值计算直到满足条件为止。

2.2 管道外部环境温度的选取

由于管道沿线情况不同，T0不再取一平均值或保守值，而是每段均取一值，同时在程序里加一数组来盛放各段埋深。若是埋地段，则数值是管道实际埋深值，而对架空段和浸水段则分别设其值为0和－1，求解过程中则利用判断句来确定管道的敷设情况并取值，若H0＞0，则调用土壤温度计算公式计算管道埋深处土壤的自然温度；若H0＝0，则T0等于大气温度；若H0＝－1，则T0等于管道周围水温。

2.3 管道正常运行过程中K 值的计算

为了计算的准确性，此处K 值并不是取整个管道的平均值，而是根据公式

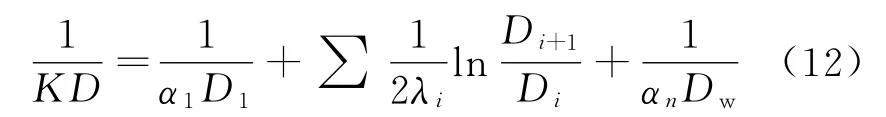
来计算每一个节点的K 值，然后用此值来代替整个计算管段的平均值。这里通过迭代的方式来求解K 值，具体思路如下：

①设管道内壁温度为Tb，根据油流至管内壁的放热系数的计算公式求解出α1；②根据公式（12）求解K 值；③根据Q＝KπD（Ty－T0）求出稳定传热的散热量；④根据热平衡关系可以求得Tb1＝Ty－Q／（α1πd）；⑤将Tb和Tb1进行比较，如果两者差别较大，将Tb1赋给Tb，重复①-④，直到两者误差在允许范围之内，此时所得K 值就是计算所用值。

2.4 管外介质的处理

2.4.1 计算区域的确定 对埋地管道而言，其在土壤中的热量传递实际上是热量在半无限大介质中的传递过程，针对此问题，有限元的处理方法是截取一个较大的计算范围，在外边界给出近似的边界条件。目前这一求解区域一般都是通过试算来确定的。而对于架空段或浸水段，其所需求解的区域实际上是管道中心与管道最外层所确定的区域，这里为了使整个管道统一使用一套计算网格，给其假定了一个虚拟的大于零的热影响半径。这样在求解过程中，有限单元自动剖分程序只需调用一次即可。其中埋地管段的几何模型见图1，而对于浸水段和架空段而言，其几何模型与埋地段类似，只是r0与rn之间的区域是虚拟的。而网格划分见图2。

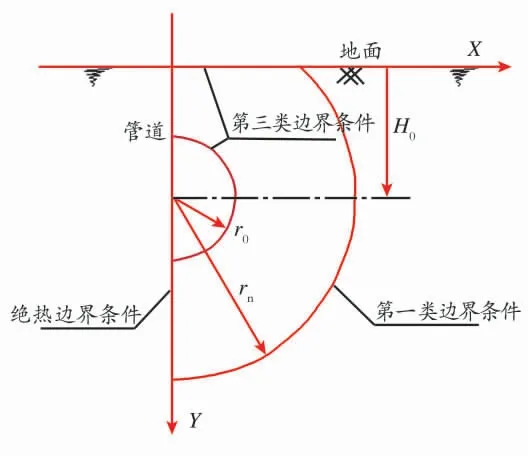
图1 埋地管道的几何模型Fig.1 Geometrical model of buried pipe

2.4.2 温度场的求解 由于浸水段（架空段）在介质中的网格是虚拟的，如果按照有限元的一般方法求解势必会使计算结果与实际存在很大的差距。这里把这几部分网格当作第一类边界条件来处理，具体计算方法见文献［6，10］。

图2 计算区域和网格划分Fig.2 Calculation area and drawing meshes

3 算例分析

某实际管线全长69.4km，管径尺寸为φ377 mm×7mm，管道无保温，全线采用埋地敷设，管道平均埋深为1.5 m。但在距起始端约52km 到62 km 处存在约10km 的浸水管段，管道正常运行过程中出站温度为68 ℃，管道流量为7 320t／d。管外土壤平均导热系数为2.6 W／（m·℃），密度为1 900kg／m3，比热容为1 420J／（kg·℃）。管道埋深处土壤温度为21 ℃，浸水段水温为16 ℃。

利用本文方法对该管道处于正常运行以及停输再启动过程中油流温度的变化特点进行了模拟计算，具体结果见图3。

3.1 特殊管段对原油管道正常运行过程中热力特性的影响

图3表示的是特殊管段对处于正常运行的管道热力特性的影响。由图3可知，结蜡层的存在使得管道内油流向周围介质的散热能力减弱，沿线油温下降趋势减缓；而浸水段的存在则使油流的沿线温降急剧增大，导致管道末端温度有较大的降低；若在计算中忽略这些特点，势必会导致停输计划的失误，从而给管道的安全带来极大的威胁。

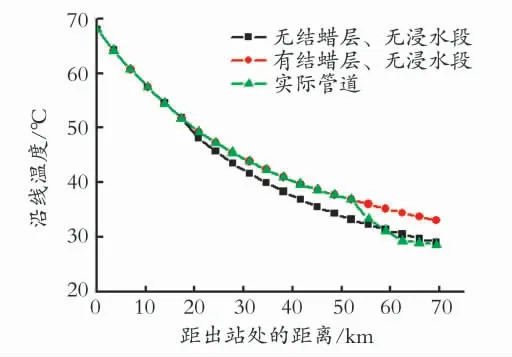
图3 特殊管段对正常运行管道沿线油温的影响Fig.3 Effect of special pipe sections for the oil temperature along the pipeline which is in stable operation

3.2 特殊管段对原油管道停输过程中热力特性的影响

图4表示的是不同条件下管道停输12h后的沿线油温分布。由图4可见，虽然在正常运行过程中含结蜡段的管道油温较高，但停输12h后，其中间一段管线的温度反而低于未结蜡管道的温度，说明管道结蜡后，原油在管道停输后温降速度要快得多。这是因为管段结蜡后使得管道在运行过程中形成的土壤温度场偏低，土壤蓄热量偏小，相对结蜡层的保温作用，土壤温度场对原油温降的影响更明显。但由于在管道正常运行过程中，结蜡管道内的油温偏高，所以停输时间较短时，其管道沿线温度还是比未结蜡管道内原油的温度高，随着时间的延长，就会出现温度的交叉（见图4），当停输时间延长到一定的程度时，结蜡管道整个结蜡段内的油温都会低于未结蜡管道，即结蜡段的存在对管道长时间的停输是不利的。而浸水管段的存在使得管道停输后的沿线温度更为复杂，在停输12h的条件下，浸水段的油温已远远低于管道末站的油流温度，这给管道的再启动过程带来了未知的危险因素，严重影响着停输管道的顺利再启动。

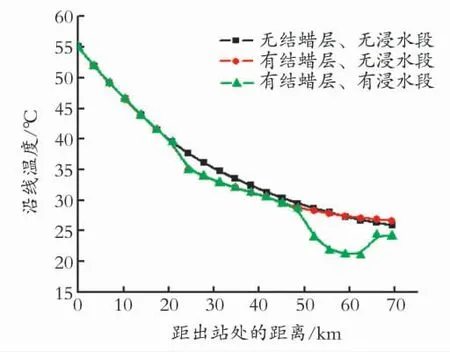
图4 不同条件下管道停输12h后的沿线油温分布Fig.4 Oil temperature along pipeline after shutdown for 12 h under different conditions

3.3 特殊管段对再启动管道热力特性的影响

图5表示的是不同条件下管道末端油温随启动时间的变化规律以及与实测值的对比。由图5 可见，在以上三种模拟条件下，第一种条件下（无结蜡层且无浸水段）得到的油温变化规律最为简单，油流温度仅通过三个阶段的变化就可达到稳定状态。开始阶段，管道末端油温缓慢增加，在热油头到达后，其油温会有明显的增加，随后经过一段很短的时间，油温增加趋势变缓直至恒定；第二种条件（有结蜡层无浸水段）下，随着启动时间的延续，管道末端油温会出现两次温度的跳跃，第一次的跳跃是因为结蜡层的存在使得管道在停输过程中，结蜡管段与未结蜡管段之间出现较大的温度差距，第二次温度的急升则是因为管道出站处热油头的到达；第三种条件（按管道实际情况）下模拟得出的油流温度数据以及变化规律与实测值最为接近（最大相对误差为7.94%），过程也最复杂，在整个启动过程中，管道末端油温会出现三个阶段的平稳变化，一个阶段的急剧下降和三次油流温度的急剧增加，出现这种现象是因为浸水段和结蜡段的存在使的管道沿线油温在停输过程中出现多次较大的起伏。

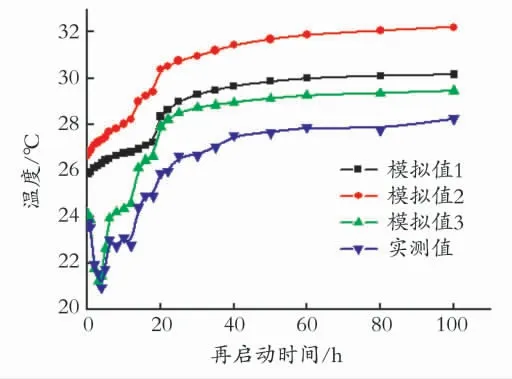
图5 管道末端油温随启动时间的变化关系Fig.5 Variation of oil temperature at the end of pipeline with starting time

此外，随季节、油流温度、土壤导热系数、管道结蜡规律以及特殊管段所在位置的不同，这些特殊管段对埋地油管道热力特性的影响可能不尽相同，但值得注意的是在对管道（特别是长距离管道或气候比较恶劣的地区或季节）进行模拟计算时，一定要考虑特殊管段的影响，否则很有可能引起重大的安全事故。

4 结论

（1）对含特殊管段的管道进行了整体研究，提出不同管段需利用不同T0计算，并利用一维数组解决了求解的困难；对埋地管段，提出不同埋深利用不同热影响半径，而对架空段和浸水段，则采用虚拟热影响区的方法。

（2）结蜡层的存在虽然使管道在正常运行过程中，其内部油流向管外的热损失减小，同时也使得管道在运行过程中形成的土壤温度场偏低，土壤蓄热量偏小，因此管内原油在管道停输过程中温降幅度变大，不利于管道的顺利再启动。

（3）管道沿线存在浸水段时，不仅会使管道正常运行过程中末端油温偏低，且当管道处于停输状态时，还会使处于管道中间浸水段的油温远远低于管道末端油温，严重影响了对停输管道顺利再启动的判断。

［1］ 赵会军，张青松.热油管道停输过程土壤温度场PHOENICS 数值模拟［J］.石油化工高等学校学报，2006，19（4）：76－79.

［2］ Davidson M R，Nguyen D，Chang C，et al.A model for restart of a pipeline with compressible gelled waxy crude oil［J］.J.non－Newtonian Fluid Mech.，2004，123：269－280.

［3］ Venkatesana R，Nagarajanb N R.The strength of paraffin gels formed under static and flow conditions［J］.Chemical Engineering Science，2005，60：3587－3598.

［4］ 江国业，张文信，周诗岽，等.低输量输油管道的清蜡周期研究［J］.抚顺石油学院学报，2003，23（3）：46－49.

［5］ 吴明，江国业.输油管道土壤温度场的数值计算［J］.石油化工高等学校学报，2001，14（4）：54－57.

［6］ 林名桢，李传宪，杨飞.管道埋深对稳定运行热油管道热力特性的影响［J］.石油化工高等学校学报，2008，21（3）：63－67.

［7］ 刑晓凯，张国忠.埋地热油管道停输与再启动过程研究［J］.石油规划设计，2001，12（3）：21－23.

［8］ 崔慧，吴长春.热油管道非稳态工况传热与流动的耦合计算模型［J］.石油大学学报：自然科学版，2005，29（3）：101－105.

［9］ 林名桢.含蜡原油输送管道再启动模型的研究［D］.东营：中国石油大学（华东）硕士论文，2007.

［10］ 孔祥谦.有限单元法在传热学中的应用［M］.北京：科学出版社，1998.