基于支持向量机和遗传算法的刀具故障诊断

王 姣，刘海燕

(大连交通大学 软件学院，辽宁 大连 116028)

0 引言

随着集成制造技术的不断进步，数控机床也逐渐向高智能、高速度、多功能、网络化的方向发展。同时，在数控机床中刀具的故障也逐渐成为生产过程中的瓶颈之一。

支持向量机的机器学习方法通过结构风险最小化归纳原理来控制学习单元的VC 维上界，同时，支持向量机能够有效解决例如小样本，非线性和高效模式识别的实际问题。支持向量机还具有神经网络无法比拟的优点，网络结构和神经网络相比较容易确定，收敛速度相对较快，并且训练时不需要大量数据，而遗传算法也同时具有很多优点［1-3］，该方法以生物进化为原型，具有很好的收敛性，在有计算精度要求时，计算时间少，鲁棒性高。所以，适合应用于参数的选择和优化［4-6］。实验结果表明，两种方法结合对于故障诊断切实有效，为刀具故障的诊断提供了一种新的方法。

1 支持向量机状态识别算法及核函数

支持向量机的原理就是通过核函数将需要输入的向量映射到一个高维特征间，接着选择分类决策函数，然后在新的高维特征空间中构造最优分类面［7］。最终得到分类结果。基于支持向量机的状态识别步骤如下:

(1)按照一定的准则和诊断策略对前期提取出的能够准确表达设备状态的信息，进行训练。

(2)输出分类结果。

(3)根据分类的结果确定设备的状态。分类问题求解时，需要选择不同的映射核函数，相似性和相似程度的评价标准就不同现在常用的核函数有:

多项式核函数:

其中C ≥0，d 为任意正数。Gauss 径向基核函数:

Sigmoid 核函数:

其中α ＞0，β ＞0。

在样本较小的情况下，SVM 能够由得到有效的分类结果。SVM 的状态识别系统就是类似于一个黑匣子的模型，所以在应用的过程中往往不必关心该模型内部的具体结构是怎么样的，因此我们只需要关注输出和输入。同时，输出和输入之间的映射结构是由支持向量机算法完成的。

2 遗传算法与数学建模

2.1 遗传算法的基本原理

遗传算法从代表问题可能潜在的解集的一个种群出发，然而，一个种群是由经过基因编码的一定数目的个体组成。每个个体实际上是染色体带有特征的实体。染色体作为遗传物质的主要载体，因此，在一开始需要实现从表现型到基因型的映射即编码工作。由于仿照基因编码的工作很复杂，我们往往进行简化，初代种群产生之后，按照达尔文的关于生物进化的关于适者生存和优胜劣汰的原理，逐代进化逐步产生出越来越好的近似解。

2.2 数学建模

利用遗传算法进行求得最优解时，要根据实验要求进行数据建模。本实验在求得遗传算法的适应函数时，就要进行数学建模［8］。本文选取斜率指数模型进行建模。首先在单输入及单极点的情况下，新的数学模型为:

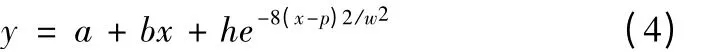
在多输入多极点的情况下，数学模型为:

对于(5)式，其中a 表示系统的控制常量，b 表示线性变化的趋势项，h 代表系统极值点的位置，p 表示极值点的高度，w 表示机制点的宽度，n 为输入项的数目，m 为n 维空间的峰值的数目。因为该数学模型是由斜率函数和指数函数构成，所以，称该模型是斜率指数型模型(SEM)。

在建立数学模型后，接下来就要对参数求解，在本实验中我们将应用最小二乘条件下的优化解方法。因为该优化解方法能够考虑到综合误差又能考虑到局部的最大误差。一般来说，如果假设实验数据集为y 对于给定的y，设模型为:

采用最小二乘条件下的优化解方法找到:

上式中的最小解就可以得到a，b，h，p，w. 其中式(7)为本实验遗传算法的适应度函数。

3 实验及结果分析

3.1 实验仿真

为了验证支持向量机和遗传算法在数控机床刀具故障的应用可行性，我们对刀具在正常工作和磨损的两种状态下的数据进行分类比较识别。本文以文献［9］中表1 中的部分数据作为样本数据，表2 中的部分数据作为测试数据，并将本文涉及的方法运用到刀具磨损状态识别中去。

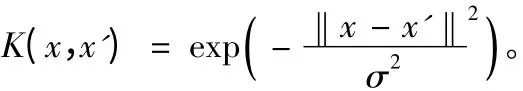
表1 C 的取值对实验结果的影响

当C = 8000 时，σ2的取值对实验结果的影响。

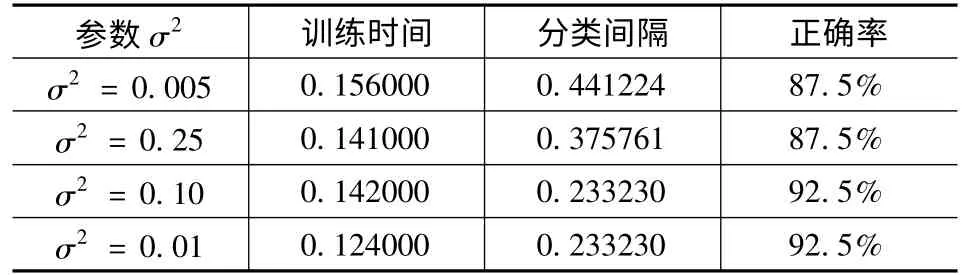
表2 σ2 的取值对实验结果的影响

用MATLAB 的工具箱对实验结果和预期结果进行比较。

图1 MATLAB 对采用SVM 实验结果与预期结果对比图

从以上实验结果可以看出，支持向量机的正确率和我们所期望的相比较，有相当高的准确率。当C= 8000，σ2= 0.01 时的训练时间、分类间隔、支持向量个数和分类正确率都趋于稳定，且达到了92.5%的分类正确率。C 是支持向量机分类器的重要控制参数，从理论上讲，在确定的数据子空间中。C 的取值越小，表示对经验误差的惩罚越小。正确选取惩罚因子C 和σ2是至关重要的，也是比较繁琐的过程。现在C和σ2选取的过程是试凑，是多次试验反复比较的结果。所以，为了能够在较短的时间内找到合适的参数值，我们用遗传算法来对支持向量机的核函数的参数进行快速优化。

(1)应用遗传算法，首先要解决编码问题，编码质量的好坏将直接影响到后续实验的进行。在本实验中我们应用二进制编码方法对个体进行编码。在编码之前要先了解一下染色体结构。

图2 染色体结构示意图

图中Fi表示是否被选做支持向量机的输入。若值为1 则选中，为0 表示落选。C 表示惩罚因子。K 表示核函数的参数。适应度函数总是非负的，而且其值越大越好。从本实验而言，设计的适应度函数为f(a，bi，hj，pi，j，wi，j)= ∑(S－y)2，经研究分析，得出较少的故障特征和较高的诊断精度所对应的适应值也较高。那些能够用较少的故障特征来获得诊断精度的个体就会以较大的概率被遗传到下一代。

(2)对种群初始化，一般对于遗传算法而言，初始个体是随机产生的，并不是个体的数目越大越好也不是越小越好。如果数目较大，收敛过程比较慢，比较难以得到最优解，如果数目太小，就会出现收敛的局部最优化问题。总之，个体的选择要视具体情况而定，选择合适的个体数目。

(3)计算个体的适应度，在依据个体的表现性设定支持向量机的惩罚参数以及相应的核函数之前，一定不要忘记先对其进行解码。

(4)确定参数和遗传算子，为了避免适应度较高的个体在较短的时间内占据种群以及避免适应度较差的个体停止进化，首先在确定遗传算子前，要对个体的适应度进行排序，然后按一定的比例进行复制［10］，最后确定交叉概率。在遗传算法中交叉率一般在0.4 到0.99，这样能够产生新的个体，一般设定为0.0001 到0.1，这样既能产生新的个体，又可以维持种群的多样性，防止早熟现象的出现。

本实验用MATLAB 工具箱设定参数并得到最优解。本实验设定样本的个数为30，迭代次数为20，染色体长度为10.交叉概率为0.6。变异因子为0.001，当满足进化条件时终止，从而得到最优化的染色体以及适应度为1.08，与之对应的惩罚函数C 的最优解为8203，核函数的参数σ2为0.01，故障的精度为96.4%。

3.2 实验分析

为了比较本文方法的优越性，特别设计了RBF神经网络的故障诊断方法。选取相同的测试和训练样本，进行分解，提取各个节点的能量并组成特征向量，然后利用RBF 神经网进行刀具故障诊断。与本文方法的比较结果见表3。可以看出，RBF 神经网络的故障诊断方法不能有效的区分正常与故障的两种刀具状态，并且仿真过程中，支持向量机在收敛速度和分类性能上，尤其是在小样本分类情况下，要明显优于RBF 神经网络。从时间角度比较，由于本文采用遗传算法进行参数优化，和RBF 神经网络相比较有效地节省了实验的时间，提高了效率，见图3，图4。

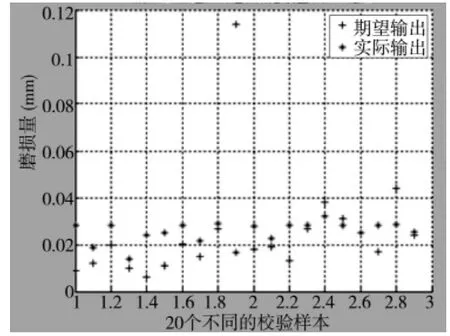
图3 RBF 进行刀具磨损量识别结果图表3 本文方法和RBF 方法比较

图4 SVM 进行刀具磨损量识别结果图

方法 样本数 测试样本数分类结果正常数分类结果故障数准确率SVM 20 20 17 19 92.5%RBF 20 20 14 13 62.5%

4 结束语

本文提出的基于支持向量机和遗传算法方法的各自优点以及数控机床中出现的故障特点，同时把本文的方法和RBF 神经网络方法加以比较。结果发现，支持向量机和遗传算法的结合明显优于RBF 神经网络。为数控机床的刀具诊断提供了一种切实有效的方法。

［1］贾伟广，胡丹，车畅. 基于小波分析 和支持向量机的刀具故障诊断［J］. 组合机床与自动化加工技术，2010(12):65－70.

［2］金珠，马小平. 基于云模型的最接近 支持向量机增量学习方法［J］. 计算机应用研究，2011，28(5):1165－1191.

［3］张学工. 关于统计学习理论与支持向 量机［J］. 自动化学报，2000，26(1):33－42.

［4］刘勇，康立山，陈毓屏. 非数值并行算法——遗传算法［M］. 北京:科学出版社，2000.

［5］Samanta B.Artificial networks and genetic algorithms for gear fault detection［J］. Mechanical System and Signal Processing，2004(18):1273－1282.

［6］Zhang L，Jack I B，Nandi A K.Fault detection using genetic progrming［J］. Mechanical System and Signal Processing，2005(19):271－289.

［7］阎平凡，张长永. 人工神经网络与模拟进化计算［M］. 北京:清华大学出版社，2005.

［8］赵世平，廖俊必，袁中凡. 基于遗传算法的实验数据建模［M］. 哈尔滨:哈尔滨工业大学出版社，2005.

［9］路勇. 加工工况信息远程监测与刀具损识别技术的研究［D］. 哈尔滨:哈尔滨工业大学，2000.

［10］雷英杰，张善文，李续武，等. Matlab 遗传算法工具箱及应用［M］. 西安:西安电子科技大学出版社，2005.