基于贝叶斯网络的智能装配技术

张 帅，陈 虎，左平基

(海军工程大学 船舶与动力学院，武汉 430033)

0 引言

智能装配作为现代设计中一项重要的技术，正日益突显出它不可或缺的地位。在提高设计效率和缩短生产周期方面发挥着相当大的作用。目前，有很多关于此方面的研究，例如智能装配导航技术［1］、智能自动定位技术［2］、自动识别装配约束技术［3］、基于装配特征的快速装配技术［4］、语义推理的装配技术以及对模型属性信息扩充的装配技术［5-6］。这些技术在日常的设计工作中已经起到了很大的作用，但是它们自身还存在着一些问题:仍需要一定的交互操作;需要扩充大量的特征信息;可推理的装配体种类的局限性。

以往的这些智能装配技术大都是对典型装配体归类和总结，或者是对装配体的三维模型信息的共同特征进行分析归纳，然后得出一般的推理规律。所得到的这些规律在很大程度上具有一定的局限性。在这其中会不可避免的遗漏掉一些相对分散的不确定的装配推理因素。因此，为了能够将这些因素包含到装配推理的过程当中，本文建立了以贝叶斯网络为基础的装配推理过程。贝叶斯网络是采用有向图来描述概率关系的理论，它适用于不确定性和概率性事物，应用于有条件地依赖多种控制因素的相关问题，能够在不完全、不精确或不确定的知识和信息中作出推理和判断［7-10］。为了增强对未知装配体推理能力，本文还建立了自动识别零件的识别库。识别库通过对零件的特征自动识别和分类，产生更好的训练样本，从而提高构建的BN 的鲁棒性。结合上述两种方法，本文提出了一个能够对已有的装配体的学习和记忆以及对未知装配体的推理和识别的智能装配技术。

1 装配推理过程

本文总结得出的装配推理过程:先确定零件自身的装配约束方式，再由装配模式得出两零件的配合方式，再由配合方式推出配合面片，最后施加约束。

常用装配方式的基本上可以分为两大类:紧固件连接的装配方式和非紧固件连接的装配方式。由紧固件连接的装配件可以推导出两零件的配合的特征是孔配合和定位面的配合。而非紧固件连接的装配体就需要分析零件三维模型的面片信息(包括面片类型和面片数量)并结合面片与约束的关系，推导出它的一般常用的配合模式。再从两零件自身的装配约束方式中提取出相同的约束方式作为他们的装配配合模式，与此同时也得到了配合面片。最后对相应的面片的施加相应的约束即可。推理过程如图1。

图1 缺少图片说明

2 装配推理模型

2.1 构建贝叶斯网络

在上述的装配推理中，有相当一部分零件无论是在三维形体上还是在装配模式上都没有太多的共同特征，如果对这些零件进行较为准确的分类和识别是相当困难的，以往的很多智能装配技术省略这些因素。同时，这在很大程度上阻碍着装配推理进行。所以在对这些零件进行识别和确定约束时需要以一定的装配经验和自身三维模型的面片特征相结合作为推理基础。而装配经验的获得是对大量已有装配体的学习上逐渐积累起来的。因此本文针对此装配推理过程建立了装配推理的BN。用概率的大小去对这些因素进行处理从而解决准确分类和识别的问题。BN 是对逻辑事件之间的一种概率推算，通过事件之间的逻辑网络进行概率传播。BN 以现有的大量的样本计算出各节点的先验概率，当有新的条件概率加入某一节点时，可以推理出其他节概率信息。然后从各节点中提取概率相对较大的事件作参考。

紧固件连接的装配推理是较为简单的，只需要找出配合孔相对应的圆柱面片和配合定位面的平面面片，然后对它们分别施加圆柱面片的轴线对齐和平面的配对即可。非紧固件连接的装配推理过程就相对复杂一点。此过程需要对零件自身的面片信息直接进行处理。在一般装配环境下常用的装配配合有:相切、贴合、对齐、共轴等。而模型面片的类型与装配约束之间必然存在着一定的关系:

(1)平面与平面的位置关系:配对，对齐，偏置，平行，垂直。

(2)柱面与柱面(旋转面与旋转面)的位置关系:配对，共轴，相切(轴线平行或垂直)，平行。

(3)球面与球面的位置关系:配对，相切。

(4)平面与柱面的位置关系:相切(轴线平行或垂直)，垂直。

(5)球面与平面的位置关系:相切。

除了面片与约束之间存在一定关系外，配合的面片之间也还需要一定的结构尺寸配合关系，例如配对的两个柱面的半径一般应该是相等的，对于配合的两个球面来说半径一般也是相等的。面片配合还存在着一定的优先级别。这种级别是按照配合的约束的自由度的数量进行排列的，约束的自由度越多，优先级别越高。一般的顺序:柱面与柱面、球面与球面、平面与平面、平面与柱面、球面与平面。

通过面片与面片以及面片与约束之间的关系可以对非紧固件连接的装配体进行推理。由待装配的两个零件之间的模型面片种类和数量的对应关系，从而确定出几种配合面片和对应的配合约束。基于上述推理过程构建BN，用F = {F1，F2，F3，…，Fn}表示BN 中的节点集合(见图2)，用X = {X1，X2，X3，…，Xn}表示节点变量集合。具体对应关系如表1。变量的取值有两种状态:真，假。分别用1 和0 来表示。

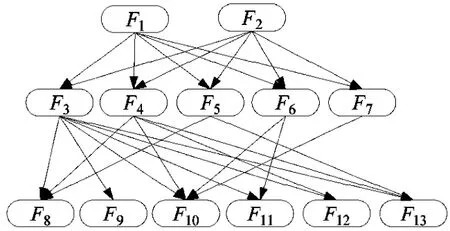
图2 BN 结构图

表1 事件与变量对应关系图

2.2 确定概率参数

根据贝叶斯网络原理:利用独立事件的关系，可以计算某种条件下的联合概率。BN 处理概率过程首要的是观察各变量相互逻辑关系。当某些变量的信息已知时就可能变成相互独立的节点，于是就能把这些条件概率替换成更小的概率项，通过计算更小的条件概率来求出联合概率。现在的常用的概率计算有很多种，本文采用的是证据相关法。此方法在计算某节点概率时，需要同时考虑到此节点的父节点集合和对此节点之后的节点集合。计算结果要在Xn的整个空间上进行归一化以表示概率。

2.3 建立零件识别库

对于贝叶斯网络的各节点的概率确定需要对历史样本进行分析和总结。这些样本具体来说就是已有的装配体中的各零件的装配信息和它们的三维本身信息。由于这些样本包括了各种装配体的装配模式，所以如果对任意一种待装配的零件直接运用全部样本来确定节点概率的话，就会产生冗余计算，而且会使网络变得不稳定，最后得到结果概率的倾向性会很差。为了解决这种情况，需要对样本做分类处理，即对不同的待装配的零件使用相应的样本去确定网络的节点概率。具体来说就是对已有的装配体的零件进行特征识别，并把装配类型相似的装配体分别归类保存。依据此规则，建立了零件识别库。

识别库是对装配的两个零件的面片类型和它们的装配约束进行识别。同一类型装配体的要求:与待装配的零件进行比较，装配体中存在的面片类型相同，且每类面片对应的数量差在10% 之间。然后将这些信息量化，并按照矩阵的模式保存起来。每个矩阵表示一组配对的零件:矩阵每一列的信息都对应着一个类型的面片，从第一列到最后一列分别对应着平面、柱面、球面，矩阵行对应的信息是两模型面片对应类型的数量以及参与配对的面片类型。

通过识别库对样本进行分类，提取出在三维形体上与待装配的零件相近的样本对网络节点概率进行确定。这样不仅能够很好的利用BN 的节点间概率传播，而且能够使网络对样本的学习速度更快。同时，识别库对装配体的相关信息的记忆作用，可以使它对装配的预测更精确。通过感知对样本变化，适时改变相关的基本条件，从而提高网络的进化速度。

3 系统实现

本系统是在UG 二次开发的基础上实现的。通过VC ++ 编程建立了智能辅助装配模块。采用Access 数据库对相关的数据信息进行存储。建立了一个模型库，其中存放着大量的装配体作为样本。装配推理时，会将其调出，利用UG 二次开发中相关函数自动对样本模型进行信息提取和转换，按照规定的格式存放到数据库中。然后依照装配的相关步骤去进行推理。

3.1 BN 推理应用

本文采用的实例是对轴承座装配过程中的其中一步的推理:

(1)根据待装配的零件面片类型和数量在历史的样本中提取相近的样本。

(2)利用这些样本对BN 各节点的参数概率进行计算，依次求出各节点变量条件概率分布。部分的条件概率分布如表2。

表2 变量条件概率分布

(3)根据待装配的两个零件的模型面片信息分别求出P(X2= 1)= 70.3，P(X3= 1)= 25.3，P(X4= 1)= 0。然后按照这几个概率去修改BN 中对应的节点参数。利用贝叶斯概率推理算法，得出其他节点的后验概率。如表3。

表3 后验概率分布

(4)最后将贝叶斯网络中的装配面片节点和装配约束节点中的概率较大的变量作为装配的所需要的要素。从表3 中可以得到概率较大的几个变量分别是:X5，X6，X10，X14，X15。以这些变量对应的名称作为参考要素进行装配。用UG 的二次开发中函数去提取参考要素中的面片，然后对相应的面片施加参考要素中对应的约束。

3.2 操作流程

(1)将装配零件导入界面。

(2)打开智能装配界面。

(3)选择要装配的两个零件。

(4)点击装配按键。在列表控件中会出现几个装配配合方式。通过分别点击这个配合方式，可以浏览零件装配模式，然后选择正确的一种。具体如图3。

图3 操作界面图

4 结束语

本文在装配推理的基础上建立了贝叶斯网络，详细的叙述了BN 的构建过程，以实例验证了其可行性。并且基于UG 的二次开发建立了智能装配系统。通过本系统的装配推理能够提高装配的速度和准确性，在一定程度上还具有装配指导的作用。

［1］万华根，高曙明，彭群生. VDVAS:一个集成的虚拟设计与虚拟装配系统［J］. 中国图象图形学报，2002，7(1):27－35.

［2］刘检华，宁汝新，姚珺，等.面向虚拟装配的零部件精确定位技术研究［J］.计算机集成制造系统，2005(4):498－502.

［3］张丹，左敦稳，焦光明，等. 面向虚拟装配的约束建模与装配意图捕捉技术［J］. 计算机集成制造系统，2010(6):1209－1213.

［4］邵晓东，殷磊，陆源，等. 一种基于特征的快速装配方法［J］. 计算机集成制造系统，2007(11):139－145.

［5］万昌江，古飚，鲁玉军. 语义推理驱动的协同装配技术［J］. 计算机集成制造系统，2010(9):1852－1858.

［6］万昌江，李仁旺. 基于端口自动匹配的产品智能装配建模技术［J］. 计算机集成制造系统，2011(7):47－54.

［7］张春民，李引珍，陈志忠，等. 基于贝叶斯网络的驼峰超速连挂事故分析［J］. 铁道学报，2011(10):8－10.

［8］胡玉胜，涂序彦，崔晓瑜，等. 基于贝叶斯网络的不确定性知识的推理方法［J］. 计算机集成制造系统——CIMS，2011(12):65－68.

［9］王中锋，王志海，付彬. 一种贝叶斯网络分类器集群式参数学习的降噪算法［J］. 模式识别与人工智能，2010(8):508－512.

［10］尹晓伟，钱文学，谢里阳. 贝叶斯网络在机械系统可靠性评估中的应用［J］. 东北大学学报，2008(4):557－560.