多目标优化与层次分析法相结合的滚齿机立柱改进设计*
徐 君,张荣闯,王 军,孙 军,于建智
(1.沈阳建筑大学 交通与机械工程学院,沈阳 110168;2.东北大学 机械工程与自动化学院,沈阳110819)
0 引言
机床立柱的结构是决定机床加工精度的关键因素,对立柱进行结构优化设计,提高机床的加工精度一直是工程师们关心的问题。一般的优化方法只是从单一目标出发,没有实现部件总体的优化设计,比如将立柱刚度最大化作为目标函数,其质量作为约束条件进行目标优化,优化的结果往往使得其他指标的改进效果不理想。
多目标优化问题是实际中常见的问题,与单目标优化问题的本质区别在于,多目标优化问题的解不是唯一的,而是存在一个最优解的集合,能够在给定的区域内使多个目标均尽可能的到达最佳的优化值。针对机床结构的多目标优化设计问题,姜衡[1]等针对结构设计动态参数设计优化展开研究,对立式加工中心主要部件进行了参数多目标优化,并采取遗传算法求取了最优解;Jan Zavrel[2]等将由两个简单部件连接的机构,通过设定左右臂的长度为设计参数,刚度和可加速度为目标函数进行多目标优化,并采取遗传算法求得了最优解。
层次分析法[3]是美国著名的运筹学家匹兹堡大学的T.L.Saaty 教授于二十世纪七十年代提出的一种多目标决策分析方法。它把复杂的决策系统层次化,通过逐层比较多种关联因素的重要性,为分析、决策提供定量的依据。其基本原理是根据问题的性质和所要达到的总目标,将其分解为不同的组成因素,依照因素间的隶属关系和相互影响,按不同层次聚集组合后形成的一个多层次分析结构模型,利用人的经验对决策方案优劣进行排序,确定每一层的全部因素相对重要的权重值,进而提出解决方案。刘世豪[4]等将层次分析法与模糊综合评判法结合,快速有效地评价了机床的整机性能指标;Z. Ayaĝ[5]运用层次分析法与仿真技术相结合,通过AHP 缩小市场上对机床产品影响因子不大的因素比例,运用仿真技术得到几组可替代的方案,通过单元选择投资成本比例得出最优方案,进而降低生产成本。
本文在分析滚齿机立柱改进前动静态特性的基础上,将多目标优化设计与层次分析法相结合,充分利用二者在结构设计上的优点对滚齿机立柱进行改进设计,将立柱改进设计前后的动静态特性进行比较,比较结果验证了本文所采用设计方法的可靠性与合理性。
1 滚齿机立柱改进设计流程
首先根据立柱结构确定影响改进指标的因素,在CAD 三维软件对立柱建立参数化模型;其次,通过AWB 与CAD 软件之间的无缝连接接口,将参数化CAD 模型直接转化为AWB DS 中的数字CAE 模型,对立柱进行动静态分析,得到立柱改进设计前的最大变形量和固有频率;然后参考立柱的原始设计变量的尺寸规划参数值变化区间,通过灵敏度分析得出优化设计变量;以立柱质量、一阶固有频率和最大变形量为目标函数,进行多目标优化。最后,采用层次分析法选出立柱高刚度和轻量化的最优参数值。图1 为立柱的改进设计流程图。

图1 立柱的改进设计流程图
2 立柱改进前动静态特性分析
通过有限元法对立柱进行动静态特性分析,得到其改进设计前的立柱变形量和固有频率。
2.1 立柱有限元模型
有限元模型的建立是动静态力学分析的基础。本文在三维CAD 软件建立立柱的几何建模同时对模型进行适当简化,略去许多不影响立柱刚度,但对网格划分产生较大影响的细微结构(如圆弧、倒角、小凸台和螺栓孔等)。选择机床立柱的材料为灰铸铁HT300,弹性模量1.3 ×1011Pa,泊松比为0.27,密度为7.35 ×103kg/m3,单元类型为Solid187 四面体单元。网格划分采用自动划分功能,结合立柱实际尺寸,将单元尺寸限定在20mm 以内。立柱有限元模型如图2 所示,共有50424 个节点,24155 个单元。

图2 立柱有限元模型
2.2 立柱静态特性分析
通过静态特性分析,可以得到立柱最大变形量。立柱载荷来自机床刀具端产生的集中切削载荷Fmax及主轴箱和滑架的重量G。本文中主轴箱及滑架的总重G=2100N。切削力与刀具类型、工件材料等有关。根据该滚齿机常用情况,选取工件材料为碳钢,计算主切削力可按以下经验公式先计算最大力矩:

式中:m——法向模数(mm);
S——轴向进给量(mm/r);
t——吃刀深度(mm);
T=t/2.25m;
V——切削速度(m/min);
D——滚刀外径(mm);
Z——工件齿数K材;
K材——工件材料系数;
K硬——螺旋角修正系数;
K螺——工件硬度修正系数。
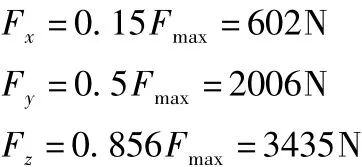
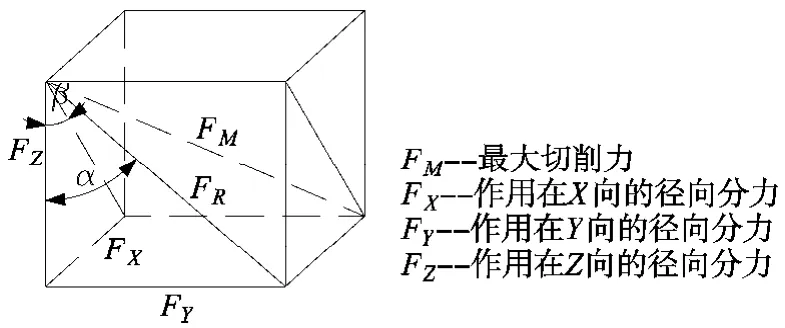
图3 切削力与分力几何关系示意图
在求出的立柱所受到的集中切削力分力与主轴箱和滑架重力后,通过力和力矩平衡将其等效为立柱导轨所承受的梯度载荷。
机床立柱底部用8 个螺栓与床身固定连接,故在底部螺栓孔处要限制所有的自由度,施加固定约束,立柱底部要防止发生扭转和滑移,因此在底面施加位移约束。图4、图5 分别为立柱在静力分析后得到的立柱位移和应力等值线图。由图4 可知,沿着立柱高度自上而下变形逐渐减小,且最大变形发生在立柱顶面与导轨相交处,最大变形接近0.029mm(小于允许值0.03mm)。图5 表明,最大主应力为9.02Mpa 远小于灰铸铁的抗拉强度,由此立柱满足强度设计要求,具有很高的安全性[6]。

图4 立柱位移等值线图

图5 立柱应力等值线图
2.3 立柱动态特性分析
模态是动力学性能的重要参数之一,用模态分析可以确定一个结构的固有频率和振型。在结构的动态分析中,各阶模态所具有的权重因子大小随模态频率的增大而减小,即低阶模态特性基本决定了该机床的动态性能。由仿真分析可得立柱的前4 阶固有频率及振型描述如表1 所示,其振型如图6 所示。

图6 立柱前四阶模态云图
滚齿机切削时主轴产生的激振频率为:
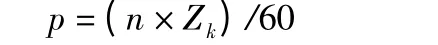
其中:n——滚刀主轴的转速(r/min);
Zk——滚刀的容屑槽数。
对于该滚齿机而言,n∈[30,300],Zk=12,经计算可得切削时的激振频率p∈[15,150]。由仿真分析结果可知,一阶固有频率大于切削产生的激振频率,避开了滚刀主轴的共振区。
大力强化国防意识培育。突出管委会和企业各级领导干部、管理骨干这个重点,推动国防理论知识进入管委会、企业管理层学习内容,军事机关组织重大活动邀请政企相关领导、骨干参加,深化其对武装工作的认识。根据经济功能区特点,结合民众关注的国际国内经济军事要点热点、国家重大经济军事政策出台等时机,突出经济建设与国防建设关系的教育,积极开展国防法规和相关知识针对性宣传教育,推动国防宣传教育融入企业文化宣传和管理要素,使员工在日常管理中受到潜移默化的国防教育,为经济功能区民兵建设营造良好社会氛围。
通过对前四阶振型的分析,前两阶主要是摆动,后两阶出现扭动,说明立柱的壁厚以及内壁筋板的厚度使得立柱的动刚度不足,须对其进行优化设计。

表1 立柱前4 阶模态计算结果
3 立柱参数灵敏度分析
在结构改进设计过程中,为了避免结构修改的盲目性,必须采用有效的控制策略。目前广泛采用设计参数的灵敏度分析。
灵敏度分析的基本原理是:通过一定的数学方法和手段,计算出结构的动静态性能参数随结构设计变量的变化灵敏度,然后选择那些对动静态特性影响较大的设计参数,并依据灵敏度值的大小正负,对设计参数值进行修正。通过其灵敏度分析,可以确定结构哪些部位的改进对提高结构动静态特性最为有效的,方便找出最敏感的结构设计参数,最终得到结构的优化设计方案[7]。根据经验,选择可优化的立柱主要尺寸如表2 所示。

表2 立柱主要尺寸
以表2 所列尺寸为设计变量,立柱静力分析的最大变形量,一阶固有频率和立柱质量为目标函数,进行灵敏度分析。图7 为设计变量对立柱输出参数的灵敏度图。
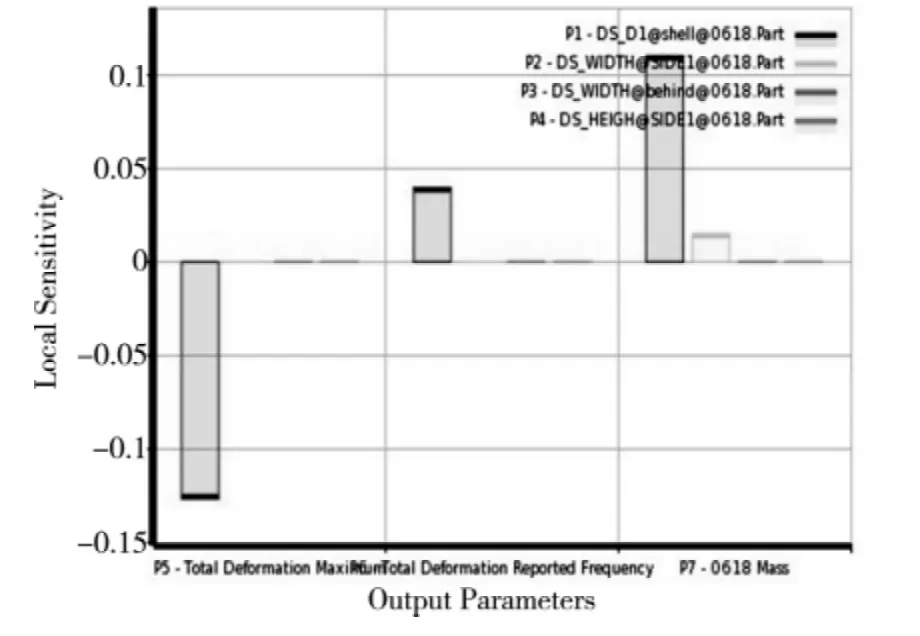
图7 设计变量对立柱输出参数的灵敏度图
图7 中,零刻度线以上的部分表示:随着尺寸的增大或减小,相应的输出参数也相应增大或减小;位于零刻度线以下的部分表示:随着尺寸的增大或减小,相应的输出参数相应减小或增大。数值越大表示对输出参数的影响越大。由图可以看出P1 和P2对立柱的质量、动静态特性有着较大影响,因此将其作为设计变量,同时将设计变量的变换范围设置为10%。图8 为设计变量P1 壁厚与P2 筋板厚对各输出参数的响应面图[8-9]。

图8 设计变量对输出参数的响应面
4 立柱多目标优化
本文立柱的优化主要采用ANSYS Workbench 软件自身的专业优化模块De-sign Xplorer 进行优化。表3 为立柱优化的目标函数和目标要求:

表3 目标函数
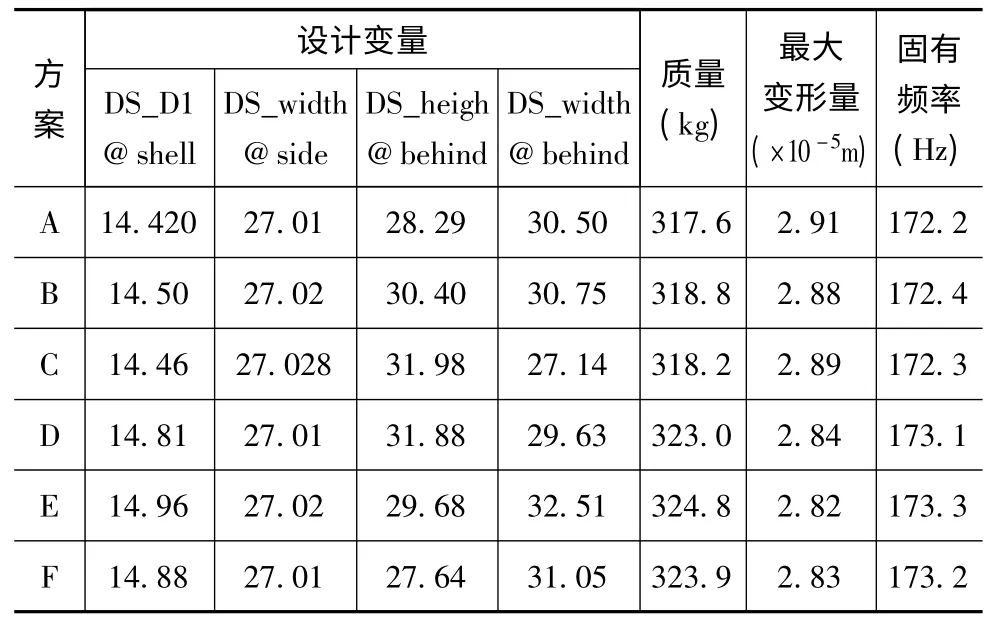
表4 六种设计方案
5 层次分析法最优方案求解
层次分析法应用主要为了从多目标优化所得到的六种设计方案中选择最优解,其具体流程如图9所示。

图9 层次分析法基本流程图
5.1 层次结构模型建立
图10 为所建立的立柱设计方案的层次结构模型。最上面的总目标层为立柱的最优设计方案;中间的准则层为立柱质量、最大变形量和固有频率;最下面的方案层为六种设计方案。

图10 立柱设计方案的层次模型
5.2 判断矩阵构建与单层权重求解
在所建立的递阶层次结构模型中,除总目标层外,每一层都是由多个元素组成,而同一层的各个元素对上一层的某一元素的影响程度不同,需要对同一层次的元素对上一级某一元素的影响程度进行判断并将其定量化。
在满足立柱的强度和精度的前提下,立柱的质量越小越好,即立柱质量的倒数越大越有优势,得到六种设计方案质量倒数矩阵:
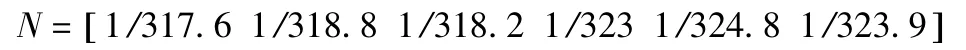
对六种方案的质量倒数两两比较,即方案A 的质量倒数除以方案A 的质量倒数得到第一行第一列的数据,方案B 的质量倒数除以方案A 的质量倒数得到第二行第一列的数据,以此类推得到矩阵:

分别对矩阵W 各列求和,得到矩阵:

将矩阵W 第1 行各列的数据分别除以矩阵Q 的对应列,求平均值,并依次对矩阵W 的各行做以上计算,得到的矩阵即为六种方案中立柱质量的优先级矩阵:
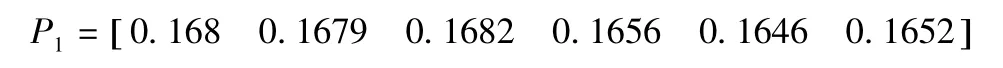
同理可得,最大变形及固有频率的优先级矩阵为矩阵P2和矩阵P3。
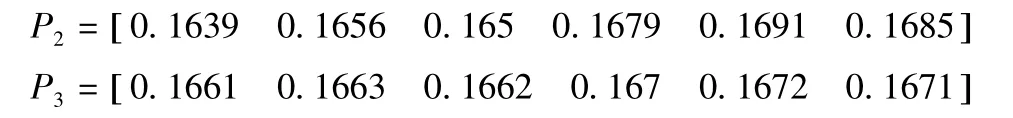
5.3 判断矩阵构建与总层权重求解
在层次分析法中一般根据萨蒂提出的“1 -9 标度方法”建立一系列的判断矩阵来计算各矩阵的最大特征值和相应的排序量值。表5 为评价立柱目标函数优先级“1 -9 标度方法”表。
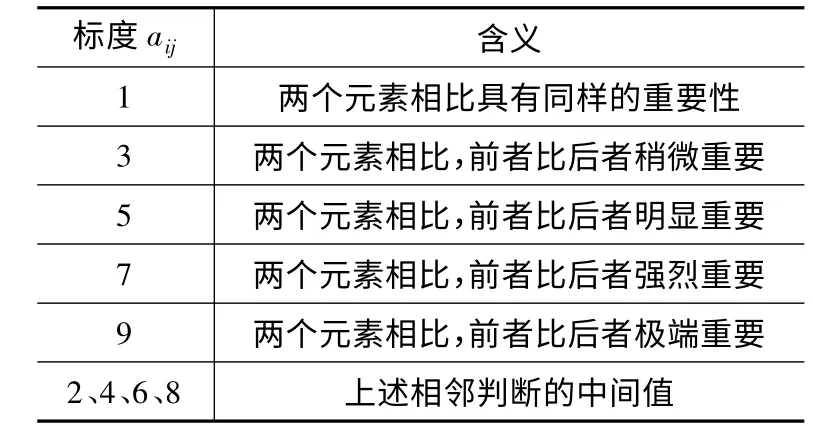
表5 “1-9 标度方法”表
根据设计者经验得到目标层各下属因素的两两比较判断矩阵I:

根据权重计算公式AT= λmaxAT(λ 为I 的特征值),求出权重因子A:
A=(4/7,2/7,1/7)
5.4 最优解的确定
将各方案对应的评判标准的优先级别与对应的评判标准的权重相乘得到各方案量化指标[ωAωBωCωDωEωF]=[0.1666 0.1671 0.167 0.1665 0.1663 0.1664]取各量化指标的最大值ω=max{ωA,ωB,ωC,ωD,ωE,ωF}=0.1671 该最大值所对应的即为方案B。将模型按方案B 的尺寸重新仿真分析,并将结果与优化前进行比较,如表6 所示。通过比较不难发现,在立柱的质量减小的情况下,立柱的动静态性能得到了一定的提高。
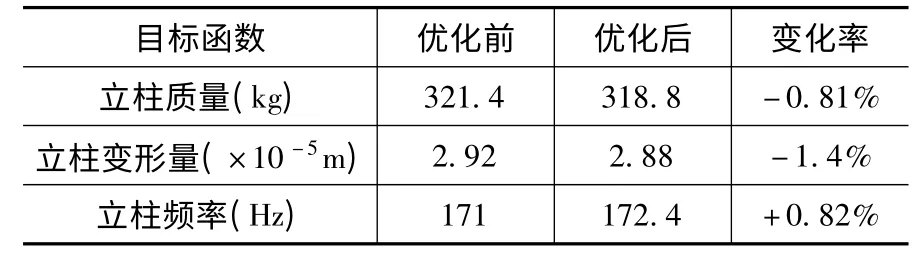
表6 优化前后结果对比
6 结论
(1)本文将多目标优化应用到滚齿机立柱结构的优化设计中,综合考虑了设计参数对动静态性能的影响,建立了以立柱质量、变形量和一阶固有频率为目标函数多目标优化模型,与单目标优化相比,使目标函数尽可能的达到了最优值。
(2)采用层次分析法对多目标优化得到的参数组合进行寻优,通过对各方案权重的计算,快速有效地评价了各方案的优劣,得到了最优解。最终在保证质量的前提下,有效的提高了立柱的动静态特性。同时该方法将多目标优化与层次分析法有效集成,改变了传统的基于部件优化方法的片面性,实现了动态优化,为产品的快速优化设计,提供了一定的参考。
[1]姜衡,管贻生,邱志成,等. 基于响应面法的立式加工中心动静态多目标优化[J]. 机械工程学报,2011,47(6):125 -133.
[2]Jan Zavrel,Michael Valasek,Zbynek Sika,et al. The Multiobjective Optimization of Mechine Tool Construction by a Global Computation in a Whole Workspace[J]. Bulletin of Applied Mechanics,2008,4(16):109 -114.
[3]T.L. Saaty. A scaling method for priorities in hierarchical structures[J]. Journal of Mathematical Psychology,1997(15):234 -281.
[4]刘世豪,叶文华,唐敦兵,等. 基于层次分析法的数控机床性能模糊综合评判[J]. 山东大学学报,2010,40(1):68 -72.
[5] Z. Ayaĝ. A hybrid approach to machine-tool selection through AHP and simulation[J]. International Journal of Production Research,2007,49(5):2029 -2050.
[6]吴凤和,乔利军,杨育林,等. 超重型数控落地铣镗床立柱结构优化研究[J]. 中国机械工程,2011,22(21):2546-2550.
[7]Fan Kuangchao,Wang Hai,Zhao Junwei. Sensitivity Analysis of the 3-PRS Parallel Kinematic Spindle Platform of a Serial-parallel Machine Tool[J]. International Journal of Machine Tools and Manufacture,2003,43(15):1561 -1569.
[8]周孜亮,王贵飞,丛明. 基于ANSYS Workbench 的主轴箱有限元分析及优化设计[J]. 组合机床与自动化加工技术,2012(3):17 -20.
[9]饶柳生,侯亮,潘勇军. 基于拓扑优化的机床立柱筋板改进[J]. 机械设计与研究,2010,26(1):87 -91.
[10]罗辉,陈蔚芳,叶文华. 机床立柱灵敏度分析及多目标优化设计[J]. 机械科学与技术,2009,28(4):487 -491.

