二维三温能量方程的RT混合线性有限元及其数值模拟

陈铁军，李跃军，肖建新

(益阳医学高等专科学校，中国益阳 413001)

二维三温辐射流体动力学方程组的求解是数值模拟的重要组成部分，而求解能量方程是一个十分重要的环节，而且在整个系统的计算中，能量方程求解所占的机时比重相当大(约80% 以上)，为此，寻求一个收敛快、稳定性好的二维三温能量方程数值解法是一个值得探讨的问题.二维三温能量方程可表示为非线性抛物型方程组，二维三温能量方程的标量式经简化得到如下方程组:

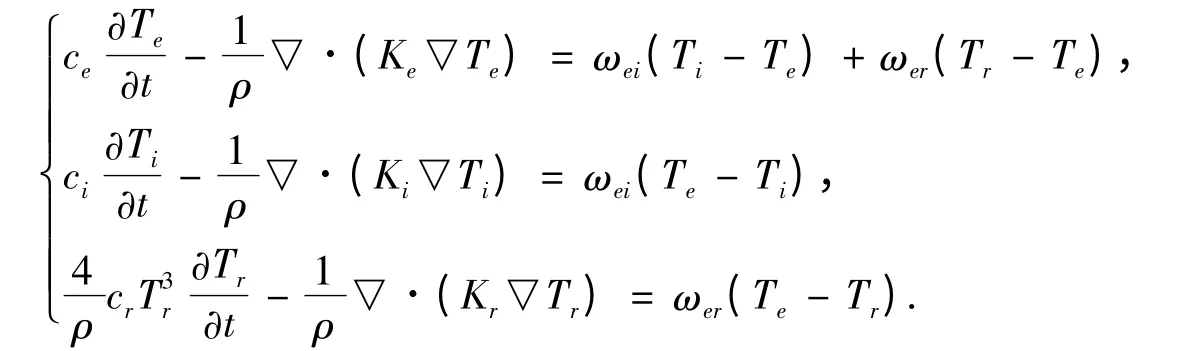
其中，Te，Ti，Tr分别为电子、离子、和光子的温度;ρ 为介质密度，在内部为常数，在介质区界面处间断;Ke，Ki，Kr分别为电子、离子和光子的热传导系数;分别为电子、离子和光子的能量交换系数，均为依赖于介质材料的常数，在介质内部连续，在介质区界面处间断.在模型方程组近似地描述了ICF 内爆动力学过程中辐射能量在静止介质中的非线性传播过程，同时也体现了原始问题的主要特性和求解的难度.

近年来，针对二维三温辐射热传导方程组的离散方法以及离散系统的快速算法设计已取得了一些成果［1-8，10-15］，利用混合有限元求解的算法文献不多，本文将主要讨论二维三温辐射热传导方程简化模型的RT混合线性有限元数值求解，获得了理想的计算结果.

考虑二维三温辐射热传导方程的简化模型问题:

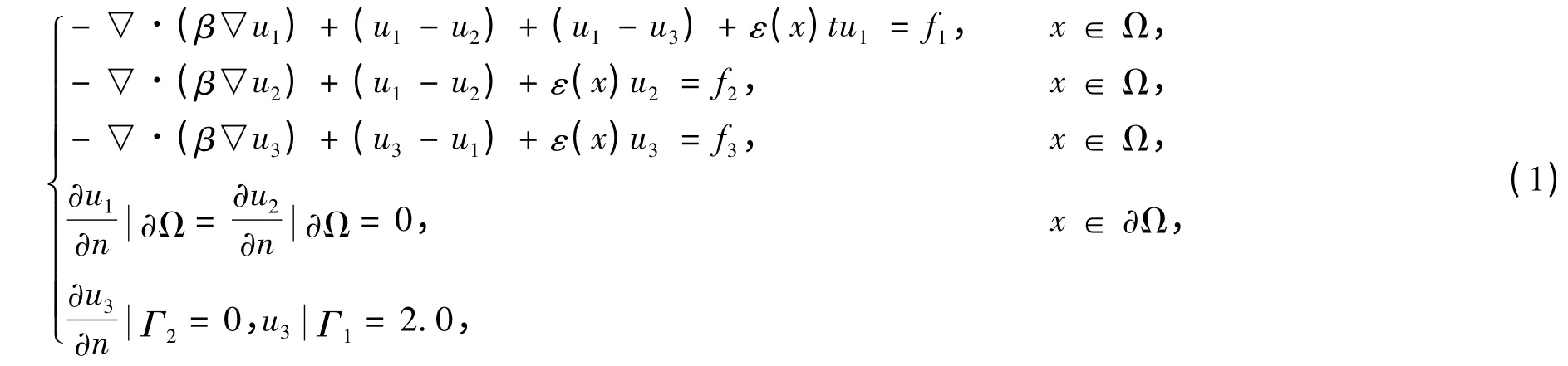
其中f1，f2，f3都是Ω 上适当光滑的函数，β ≥β0＞0，是非负光滑函数.同样考虑两片光滑函数

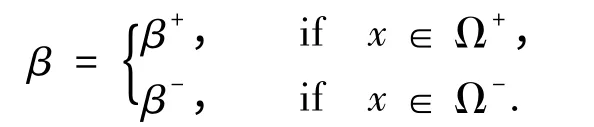
其中令Ω=Ω+∪Γ ∪Ω－，Γ 是开子区域Ω+和Ω－的交界线，∂Ω=Γ1∪Γ2且不妨假设(否则对β 的下界进行尺度化即可满足).minβ ≥β0≥1.如图1所示.

问题(1)的解函数ui∈C(Ω)(i=1，2，3)，Flux 函数β▽ui∈C(Ω)(i=1，2，3).

图1 区域示意图Fig.1 Diagrammatic sketch of area

1 连续鞍点变分问题

令p1=β▽u1，p2=β▽u2，p3=β▽u3，记p=(p1，p2，p3)T，q=(q1，q2，q3)T，u=(u1，u2，u3)T，v=(v1，v2，v3)T，f=(f1，f2，f3)T.则混合边值问题(1)等价于方程组

其中

记Y=(L2(Ω))3，相应的范数为:

定义空间

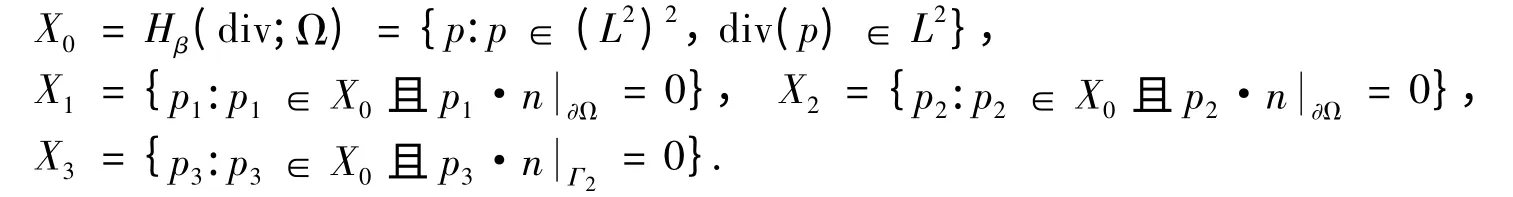
记X=X1× X2× X3，定义X 上相应的范数:

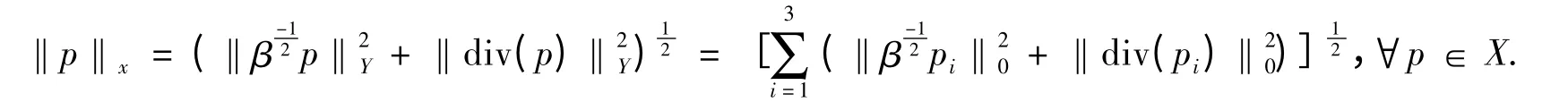
则(2)的等价连续鞍点变分问题为:

求p ∈X，u ∈Y，使

其中

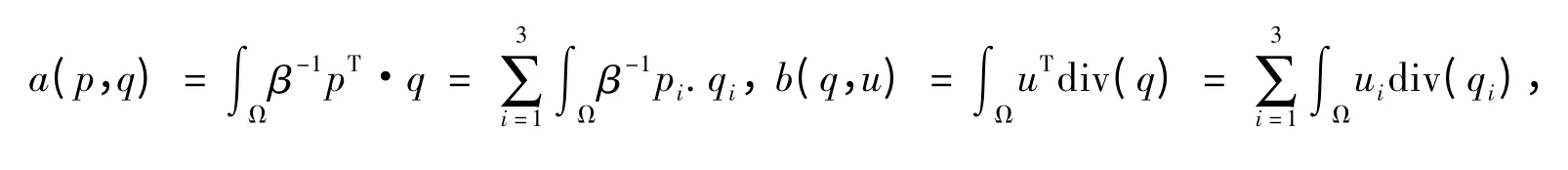
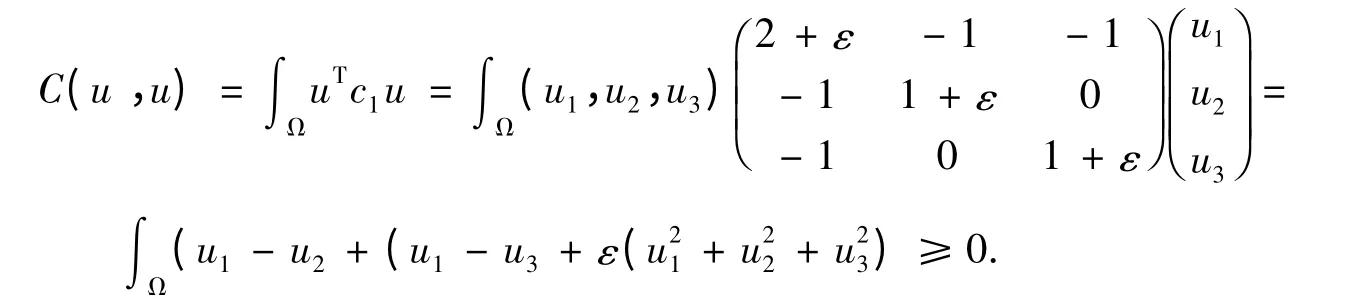
容易验证α(·，·)和b(·，·)分别是X× X 和X× Y 上的有界双线性泛函，且上界不依赖于系数β 的跳幅(因为由假设知

定理1问题(3)存在唯一解p，μ 满足

‖p‖X+‖u‖Y ≤C(‖G‖X*+‖F‖Y*)

其中C 是仅与连续双线性形式a(·，·)，b(·，·)相关的常数.

证对任意的P ∈V，由于div(p)∈Y，故有

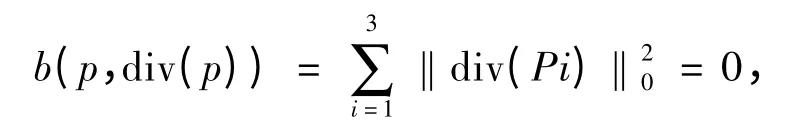
即Brezzi 定理的第一个条件成立，下面验证第二个条件亦成立.

对任意的ν ∈Y，引入辅助问题

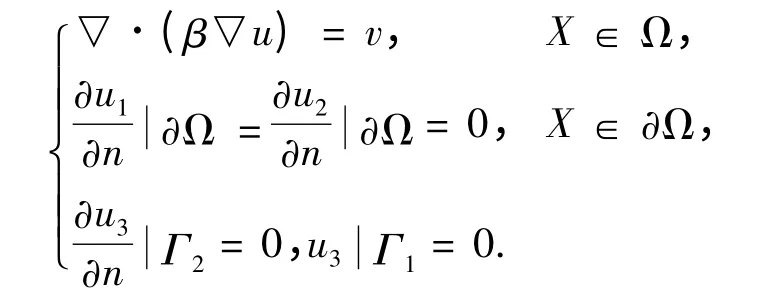
令p=β▽u，则P ∈X，且有正则性估计

其中C 只与β 的正下界β0和区域的尺寸有关.

因为，由辅助问题的定义，显然有

有

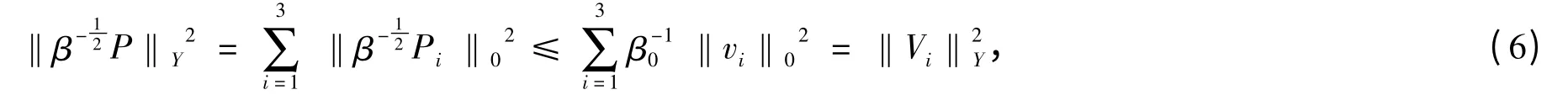
这样根据(5)和(6)，我们就证得了(4)成立，其中C 只与β 的正下界β0和区域的尺寸有关.

由(4)可知，对任意的ν ∈Y.有

其中C 只与β 的正下界β0和区域的尺寸有关

这样问题(3)的B-B 条件得到验证，因此由Brezzi 定理知结论成立.

2 对应的离散鞍点变分问题(RT 混合元)

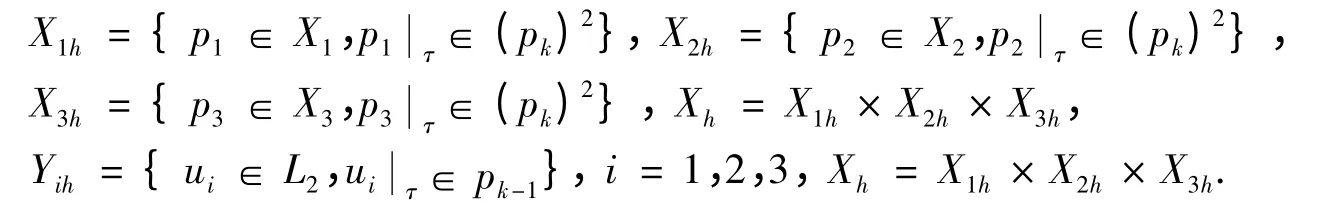
则Xh为X 的有限维子空间，Yh为Y 的有限维子空间.

本文仅考虑k=1 时的情形，我们可构造混和有限元空间Xh和Yh，于是离散鞍点变分问题为:

求ph∈Xh，uh∈Yh，使

类似标量方程，我们定义插值函数.

对任意的u ∈Y，uI表示u 在三角形剖分单元重心点处的常数插值.

对任意的p ∈Xh，其插值函数Πp 由以下条件确定:

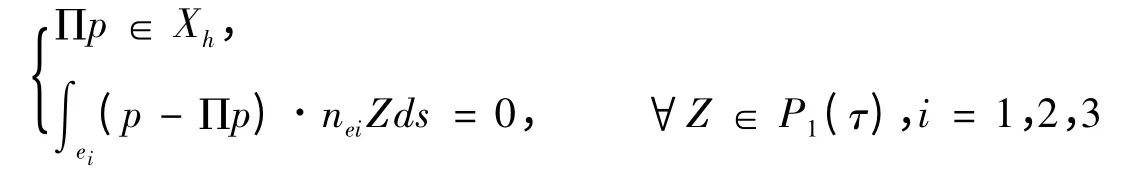
其中p1(τ)是τ 上线性多项式集合.

同样对于这样定义的插值函数，我们有以下引理

引理1设，若，则有如下误差估计

其中C 是与β 及h 都无关的常数.

证由插值函数性质有

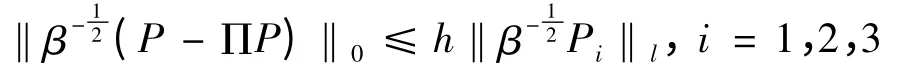
因此

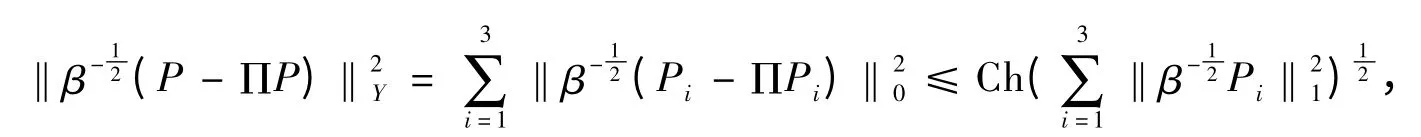
其中C 是与β 及h 都无关的常数.

定理2问题(7)存在唯一解Ph，uh满足

‖Ph‖X+‖uh‖Y≤C(‖G‖X+‖F‖Y)，

其中C 是仅与连续双线性形式a(·，·)，b(·，·)相关的常数.

证明从略.

3 误差分析

定理3问题(7)的解满足如下误差估计:

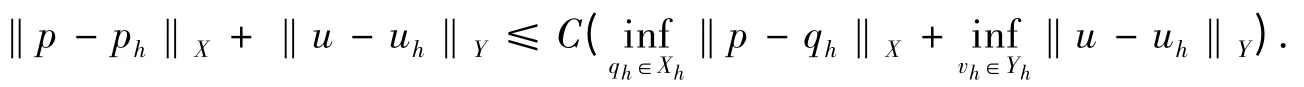
证明从略.

定理4设，若，则鞍点问题(3)和其离散问题(7)的误差满足

‖P－Ph‖x+‖u－uh‖Y=O(h).

证由定理3 知

结合引理1 和插值函数的误差估计有

定理5.

证明从略.

4 数值实验

例1考虑间断线为圆β 取为

真解为:

数值实验结果列于表1～表4.

表1 非光滑系数(α=0.1)时，真解u 与其混合有限元解uh 的误差表Tab.1 Nonsmooth coefficients(α=0.1)，the true solution u and mixed finite element error solution uh in the error table

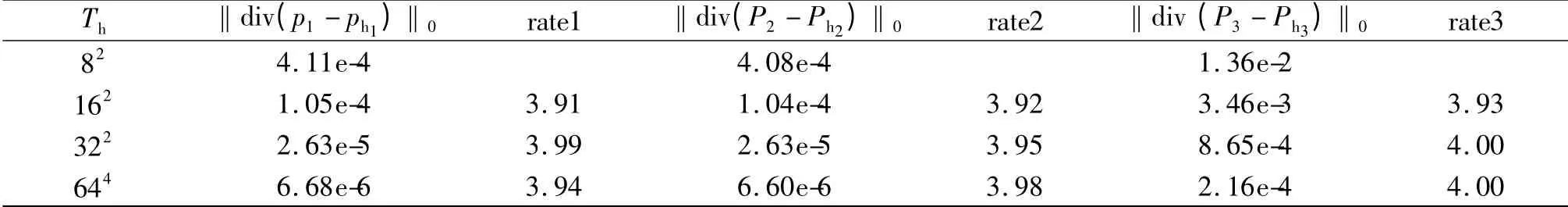
表2 非光滑系数(α=0.1)时，div(p)与其混合有限元解div(Ph)的误差表Tab.2 Nonsmooth coefficients(α=0.1)，div(p)and the mixed finite element solution of div(Ph)in the error table

表3 非光滑系数(α=0.01)时，真解u 与其混合有限元解uh 的误差表Tab.3 Nonsmooth coefficients(α=0.01)，the true solution u and mixed finite element error solution uh in the error table

表4 非光滑系数(α=0.01)时，div(p)与其混合有限元解div(Ph)的误差表Tab.4 Nonsmooth coefficients(α=0.01)，div(p)and the mixed finite element solution of div(Ph)in the error table

5 结论与展望

本文考虑了二维三温辐射热传导方程在界面处跳跃条件都连续的情形，适定性和收敛性分析中得到了最优L2阶的误差估计，从数值实验可以得到其真解u，div(p)分别与其混合有限元解存在最优差价，且最优差价与跳系数β 及剖分尺度h 均无关.另在界面处的不连续［u］Γ≠0，［βun］Γ≠0 的情况都有待深入研究.

［1］符尚武，戴自换，邬吉明.二维三温辐射流体力学Lagrange 数值模拟方法［J］.北京应用物理与计算数学研究所年报，1995，22(2):184-188.

［2］符尚武，付汉清，沈隆钧，等.二维三温能量方程的九点差分格式及其迭代解法［J］.计算物理，1998，20(3):4-8.

［3］MO Z Y，SHEN L J，GABRIEL W.Parallel adaptive multigrid algorithm for 2-D3-T diffusion equations［J］.Int J Comput Math，2004，81(3):361-374.

［4］SHEN Z J，SHEN L J，LU G X，et al.A lagrangian finite point method for two-dimensional fluid dynamic problems［J］.Chin J Comput Phys，2005，22(5):377-385.

［5］李 磊，孙 萍，罗振东.抛物方程的一种新混合有限元格式及误差分析［J］.数学物理学报，2012，32A(6):1158-1165.

［6］MA X，SHU S，ZHOU A.Symmetric finite vloume discretization for parabolic problems［J］.Comput Methods Appl Mech Engin，2003，192(39-40):4467-4485.

［7］SHU S，YU H，HUANG Y，et al.A symmetric finite volume element scheme on quadrilateral grids and superconvergence［J］.Int J Numer Analy Model，2006，3(3):348-360.

［8］谷同祥，戴自换，杭旭登，等.二维三温能量方程组的高效代数解法［J］.计算物理，2005，22(6):471-478.

［9］张恭庆，林源渠.泛函分析讲义［M］.北京:北京大学出版社，1987.

［10］魏红记，秦新强，焦建英，等.非线性反应扩散方程的两网格算法［J］.西安科技大学学报，2007，23(2):196-200.

［11］HE Y N.Taylor expansion method for nonlinear evolution equations［J］.Applied Math and Mech，2005，26(4):522-529.

［12］ABIDI F，AYADI M，OMRANI K.Stability and convergence of difference scheme for nonlinear evolutionary type equations［J］.J Appl Math Comput，2008，27(2):293-305.

［13］GEORGIOS A，FOTINI K.Modified implicit-explicit BDF methods for nonlinear parabolic equations［J］.BIT Numer Math，2003，43(2):467-483.

［14］XU C M.The stability research for the finite difference scheme of a nonlinear reaction-diffusion equation［J］.Chin Quart J Math，2008，23(2):222-227.

［15］李小松.一类非线性反应扩散方程的数值解法［J］.石河子大学学报:自然科学版，2007，25(3):382-384.