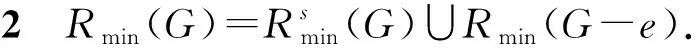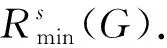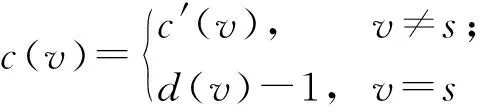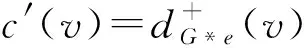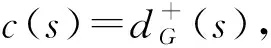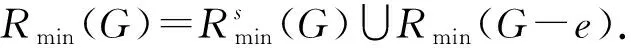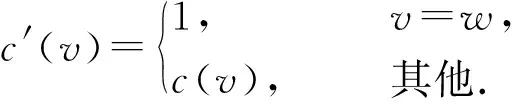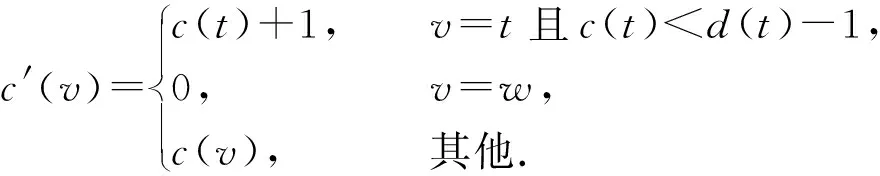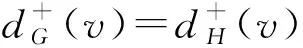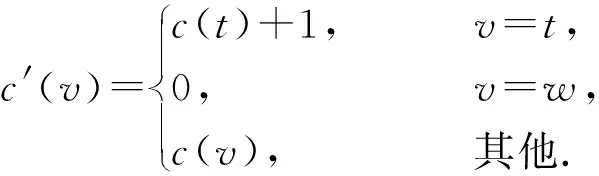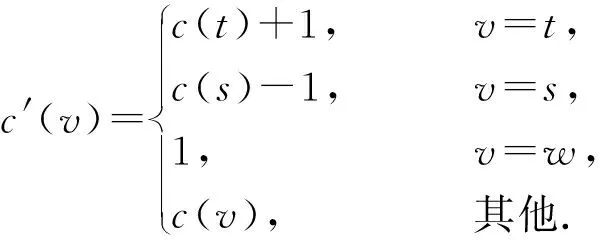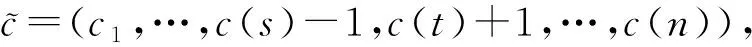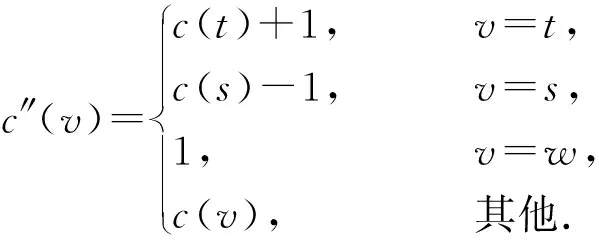图的极小循环态
孟二霞,侯耀平,方爱香
(湖南师范大学数学与计算机科学学院, 中国 长沙 410081)
早在1987年,美国的3位科学家Bak,Tang以及Wiesenfeld 在文献[1]中就提出了自组织临界性理论并介绍了一种BTW的自动机模型-沙堆模型.随后,在文献[2]中Dhar推广了这种自动机模型,提出了Abelian沙堆模型并给出了用来判断循环态的燃烧算法. Abelian沙堆模型被提出后, 许多物理学家和数学家从不同方面对这个模型进行了研究,侯耀平等在文献[3~4]中用矩阵和数论的方法确定了一些图的沙堆群结构,作为沙堆群的主要构成元素—循环态以及极小循环态有很好的性质[5].文献[6]给出了图的任一极小循环态与图G的有唯一源点q的无圈定向之间的一一对应关系. 与图上沙堆模型的循环态相关的一个问题是G-parking函数, 文献[7]给出了极大G-parking函数集的性质. 本文运用无圈定向与图的极小循环态的对应关系得到了循环态与极小循环态之间的关系以及某些图运算的极小循环态的性质.
设G=(V,q,E)是一个简单连通图,其中V=(q,v1,v2,…,vn),q是G的源点,E(G)是G的边集. 对有向图,用d+(vi)表示以点vi为起点的有向边的数目,称作点vi的出度; 用d-(vi)表示以点vi为终点的有向边的数目,称作点vi的入度,d(vi)表示点vi在图G中的度(有时候为避免混淆用dG(vi)表示点vi在图G中的度). 对于有向图中的任一点vi, 都有d+(vi)+d-(vi)=d(vi)成立. 非负整数向量u=(u(v1),u(v2),…,u(vn))称为图G的一个态,其中u(vi)表示在点vi处的沙粒数,若点vi满足u(vi) 在稳定态中,只有一部分u在某些顶点上增加一些沙粒数后经过一系列的倒塌又回到稳定态u,这部分的特殊稳定态称为循环态. 循环态在沙堆模型中具有重要的作用和很好的代数性质, 他们构成了一个有限交换群,也称为图的沙堆群. 对图G的所有循环态组成的集合记为R(G). Dhar在文献[2]中给出了判定一个稳定态u是否为循环态的有效方法, 称为燃烧算法. 燃烧算法[3]任取图G的一个稳定态u,在顶点q的每个邻点上都加1个沙粒,按照上面的倒塌规则,除点q外,若每个顶点都恰好倒塌一次最后又回到态u, 则u是图G的循环态. 对任一循环态,我们可以根据燃烧算法得到的倒塌序列来定义燃烧图. 定义1设u是图G=(V,q,E)的一个循环态,f=(v1,v2,…,vn)是图G关于循环态u的一个倒塌序列. 定义一个燃烧图Gf=(V,q,E′),其中E′={(vi,vj)|{vi,vj} ∈E∧i 另外极小循环态是一种特殊的循环态, 对图G的任一个循环态u, 称u是图G极小循环态当且仅当将循环态u的任意非零点处vi的沙粒数减少1(即u(vi)-1)时,u不是循环态. 用Rmin(G)表示图G的所有极小循环态集. 作为特殊的循环态,每个极小循环态的燃烧图有且只有1个. 下面是极小循环态与图的有唯一源点q的无圈定向间的一一对应关系. 引理1[3]一个态u是图G的一个极小循环态当且仅当存在图G的有唯一源点q的无圈定向与之对应, 使得对∀v∈V(G),有u(v)=d+(v). 本节给出循环态与极小循环态之间的关系. 将图G中的顶点标号为(q,1,2,…,n).对于任一循环态u, 根据燃烧算法可知:将与q相邻的每个顶点都增加一个沙粒,则每个顶点恰好倒塌一次最终回到u.易知循环态u的倒塌序列不唯一, 于是其燃烧图也不唯一. 但若按照下面的规则进行倒塌: 当有两个顶点同时倒塌, 则选择标号较小的顶点先倒塌,即可得到唯一的倒塌序列v1,v2,…,vn,从而得到唯一的燃烧图. 按照倒塌的先后定义偏序关系:v1 根据上述偏序关系确定图G的有唯一源点q的无圈定向: 与q关联的边都是背离q的方向,给定一顶点vj, 使得d+(vj)=u(vj),当u(vj) 下面证明按照上述方法得到的有向图O是有唯一源点q的无圈定向图. 先证明无圈: 对于包含q在内的子图,若含圈,则点q必在某个圈中,也有一条边指向点q,与前面所定义的有向图O矛盾.故点q不在任何圈中.又由u(vj)=d+(vj)且vj是尽可能指向标号较大的顶点, 若存在vi 再证该图的源点q是唯一的. 假设还存在另一源点v0, 与之关联的边也都是背离v0的,故v0在倒塌时有:u(v0)+d-(v0)≥d(v0), 而d-(v0)=0, 故u(v0)≥d(v0),与u是循环态矛盾. 假设不成立. 故图的无圈定向中源点q是唯一的. 根据上面的定理, 容易得到如下两个推论. 推论1设G=(V,q,E)是一个图,则G上的任意循环态至多是|V(G)|-1个极小循环态的并. 证根据定理1中寻找比循环态u小的极小循环态可知: 先确定1个固定的点vj, 使得d+(vj)=c(vj)=u(vj), 当vj取遍图G的所有顶点后, 至多找到|V(G)|-1个极小循环态,它们的并即为循环态u. 推论2图G=(V,q,E)中,v(≠q)是图G的1个顶点. 若整数k满足0≤k≤d(v)-1, 则存在极小循环态c∈Rmin(G),使得c(v)=k. 证任取图G的1个极小循环态c1, 在燃烧算法下,c1的倒塌序列为(vi1,vi2,…,vin), 再对图G的顶点重新标号,vij对应的标号为j, 则顶点的新序列为(1,2,…,n), 不妨设点v的标号为i,对与i关联的边定向如下: 点i指向标号尽可能大的顶点且满足d+(i)=k, 对其余的与点i关联的边都指向i. 与q关联的边都背离q, 其余的边都按标号从小到大的方向. 由定理1的证明可知,得到的有向图是有唯一源点q的无圈定向图. 再根据图的极小循环态与无圈定向之间的关系可知,存在c∈Rmin(G), 使得c(v)=k=d+(v),对其余的点v′, 有d+(v′)=c(v′). 极小循环态作为沙堆群中的特殊组成元素, 文献[6]已经给出了一些极小循环态的性质, 并且得到了一些特殊图的极小循环态.对于一般图的极小循环态,可以经过特殊图的运算得到,其极小循环态也可以由下面的定理得到. 先考虑当c(s)=d(s)-1时,图G的极小循环态可以由图G*e的极小循环态c′来得到的.定义图G上的态c: 下面考虑将图G的任意1条边分割后所得图与原图的极小循环态之间的联系. 设边e={s,t}是图G的任意一条边, 将边e分割成2条边{s,w},{w,t}得到新图H,c是图G的任意一个极小循环态.则下面的结论成立. 定理3Rmin(H)=R1∪R2, 其中R1中的元素是图H的一部分极小循环态c′,满足 R2中的元素是图H的另一部分极小循环态c′,满足 所以c′是图H的极小循环态. 这些循环态的集合记为R2. 对图G的任意一条边e={s,t}, 分割此条边后图G的有唯一源点q的无圈定向至多有3种情况,所以至多存在3个极小循环态与之对应. 前两种如上面两种情形, 另外还可以把边{s,w}定向为(w,s), 把边{w,t}定义为(t,w),当c(t)=d(t)-1时, 边{w,t}的方向必须规定为(w,t),否则点t为源点,极小循环态如R1中的形式所示;当c(t) (a) 所得到的极小循环态与(a)中的相同. 综上所述:对图G中与边{s,t}方向相反的情形若是含有圈,则没有极小循环态存在; 若得到的是有唯一源点q的无圈定向, 则其对应的极小循环态可以由前面的情况得到.于是有Rmin(H)=R1∪R2. 参考文献: [1] BAK P, TANG C, WIESENFELD K. Self-organised criticality:an explanation of 1/fnoise[J]. Phys Rev Lett, 1987,59(4):381-384. [2] DHAR D. Self-organised critical state of the sandpile automaton models[J]. Phys Rev Lett,1990,64(14):1613-1616. [3] SHEN J, HOU Y. On the sandpile group of 3×ntwisted bracelets[J]. Linear Algebra Appl, 2008,429(16):1894-1904. [5] BORGNE Y L, ROSSIN D. On the identity of the sandpile group[J]. Discrete Math, 2002,256(3):775-790. [6] SCHULZ M. Minimal recurrent configurations of chip firing games and directed acyclic graphs[J].DMTCS Proc, 2010,5(16):111-124. [7] CHEBIKIN D, PYLYAVSKYY P. A family of bijections betweenG-parking functions and spanning trees[J].Comb Theory Ser, 2005,110(1):31-41. [8] CORI R, DARTOIS A, ROSSIN D. Avalanches polynomials of some family of graphs[J]. Math Comb Sci, 2004,1(13): 81-94. [9] LOPEZ C M. Chip firing and the tutte polynomial[J].Annals of Comb, 1997,35(1):253-259. [10] BIGGS N L. Chip-Firing and the critical group of a graph[J]. Algebr Comb, 1999,9(1):25-45. [11] CHEN S, YE S K. Critical groups for homeomorphism classes of graphs[J], Discrete Math, 2009,309(1):255-258. [12] CORI R, ROSSIN D. On the sandpile group of dual graphs[J]. Eur Comb, 2000,21(5):447-459. [13] LEVINE L. The sandpile group of a tree[J]. Eur Comb, 2009,30(4):1026-1035.
1 循环态是极小循环态的并

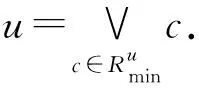
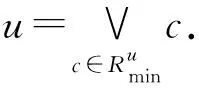
2 图运算的极小循环态