使用定向天线的无线自组网中基于粒子群优化的最大生命期广播树构造算法
沈 军 朱晓建
(东南大学计算机科学与工程学院,南京 211189)
在使用电池提供能量的无线自组网中,节能问题至关重要.使用定向天线可以使得波束集中在需要被覆盖的区域,从而可以节省节点能耗和减少传输干扰.在构造广播路由时,仅最小化总能耗可能会导致某些节点因能量消耗过快而较早地停止工作,为了最大化网络生命期需要考虑如何均衡各节点的能量消耗[1].网络生命期通常定义为直至网络中首次出现能量耗尽的节点所持续的时间[2].
文献[2-3]针对在使用全向天线时的最大生命期广播问题,提出了构造最大生命期广播树的多项式时间算法,并证明了所提算法可计算出全局最优解.虽然在使用全向天线时的最大生命期广播/多播问题是P问题,但是在使用定向天线时的最大生命期广播/多播问题却是NP完全问题[1,4].文献[4]首先证明了使用单波束定向天线的静态最大生命期多播树构造问题是一个NP完全问题,提出了一种后处理算法MLR-MD,该算法以一棵由源节点一跳直接覆盖所有目标节点的多播树开始,然后启发式地迭代改进多播树的生命期,但当在最大传输功率的限制下源节点不能直接覆盖所有目标节点时MLR-MD无法得到初始多播树.文献[5]讨论了使用定向天线的无线自组网中能量有效的多播问题,在构造最小功率多播树时考虑节点的剩余能量,增大剩余能量较少的节点的使用代价,以避免使用剩余能量较少的节点,从而延长网络生命期.文献[6]给出了在使用定向天线时的最大生命期多播树的混合整数线性规划,可用来评价启发式算法的求解质量.文献[7]提出了一种构造使用定向天线时的最大生命期多播树的D-DPMT算法,该算法在构造多播树的过程中考虑节点波束宽度最小化,在每次迭代时选择一条权重(考虑波束宽度的链路功率与节点剩余能量之比)最小的边加入多播树.D-DPMT由于直接考虑了链路生命期,所以求解质量优于文献[5]的算法.文献[8]提出了一种构造最大生命期多播树的MMT-DA算法,该算法是基于搜索-增长操作,但有向边的权重仅考虑了该有向边对应的传输半径.文献[9-10]提出了一种以节点为中心的DMMT-DA-NC算法,它是由MMT-DA发展而来,与MMT-DA以边为中心不同,有向边的权重考虑了传输节点的传输半径,在构造多播树时以节点权重为依据,其求解质量要优于MMT-DA和D-DPMT.文献[11]运用二进制离散粒子群优化算法优化最小能耗多播树的中继节点集,而最大生命期广播问题不同于最小能耗多播问题.文献[12]运用粒子群优化算法求解无线自组网中的最小能耗广播问题,而最大生命期广播问题不同于最小能耗广播问题,最大生命期是使得最小节点生命期最大化,而最小能耗是使得所有节点的能耗之和最小化.文献[13]使用粒子群优化算法求解无线自组网中的QoS多播问题,未考虑能量有效的多播生命期问题.
本文针对在使用单波束定向天线时在线的最大生命期广播路由问题,提出了一种构造最大生命期广播树的粒子群算法MLBPSO (maximum lifetime broadcast based on particle swarm optimization).该算法运用一种使用了阻尼边界条件[14-15]、EPUS-PSO[16]的粒子群体管理和解信息共享策略的粒子群算法优化最大生命期广播树的构造,并结合了DMMT-DA-NC算法构造粒子的初始位置和MLR-MD算法对粒子位置进行局部优化,有效地延长了广播树的生命期.
1 问题描述



2 粒子群优化
粒子群优化算法PSO(particle swarm optimization)[17-19]是一种随机的群体智能优化算法,每个粒子在多维空间执行搜索的过程中积累并参考自身的搜索经验和群体的搜索经验,调整自身的移动,以尽可能搜索到全局最优解.
令向量Xi={xi,1,xi,2,…,xi,D}T表示粒子i的位置,Vi={vi,1,vi,2,…,vi,D}T表示粒子i的速度,其中D表示维数.令fit(Xi)表示粒子i的适应度值,Yi={yi,1,yi,2,…,yi,D}T表示粒子i的个体极值点,即粒子i自身所经历的最好位置,则fit(Yi)表示粒子i的个体极值.所有粒子个体极值中的最优者为全局极值,令b表示个体极值最优的粒子,则Yb表示全局极值点,即所有粒子所经历的最好位置,fit(Yb)表示全局极值.在PSO[17-18]中,粒子速度Vi和粒子位置Xi按下式更新:
vi,d(t+1)=wvi,d(t)+c1rand()(yi,d(t)-xi,d(t))+
c2rand()(yb,d(t)-xi,d(t))
(1)
xi,d(t+1)=xi,d(t)+vi,d(t+1)
(2)
式中,w为惯性权重[20],用于平衡粒子群优化算法的全局探索能力和局部开发能力;c1,c2为加速因子;随机函数rand()生成在区间[0,1]上均匀分布的随机数.
为了提高粒子群优化的搜索能力和效率,文献[16]提出了一种基于粒子群高效利用策略的粒子群优化算法EPUS-PSO (efficient population utilization strategy for PSO). EPUS-PSO根据搜索状态动态调整粒子群体,当搜索状态良好时,表明当前的粒子数可能太多反而不能处理好当前的搜索步骤,应排除冗余粒子以节省进化时间,加速寻找最优解的进程,使得全局极值能够不断地进化;当搜索状态恶劣时,应新增粒子进行搜索以扩大搜索空间,增强寻优能力.令M表示当前粒子群规模.具体来讲,当全局极值在连续的λmax代内发生了一次或多次进化并且当前粒子数M>1,就排除一个较差的粒子;当全局极值连续μmax代都未进化并且粒子数量M vi,d(t+1)=wvi,d(t)+c1rand()(yi,d(t)-xi,d(t))+ (3) 式中,k以概率ρi取为从除i之外的其他粒子中随机选择的2个粒子中的个体极值较优者,以概率1-ρi取为b,其中ρi=0.5((D-1)exp((i-1)/(M-1))-1)/(2D). 运用EPUS-PSO[16]来求解MLB问题.在求解过程中,对粒子位置取整[21],使用EPUS-PSO的粒子群体管理策略动态地调整粒子群体,使用EPUS-PSO的解共享机制更新粒子速度,使用阻尼边界条件[14-15]处理粒子的越界,同时使用简化的MLR-MD算法对粒子在执行搜索过程中发现的新广播树进行局部优化以提高收敛的质量和速度. 在更新粒子位置时,通过对原粒子位置Xi(t)进行调整来得到新粒子位置Xi(t+1).首先赋值Xi(t+1)=Xi(t),然后按随机顺序处理Xi(t+1)的各维.令exrfp(Xi,u,v)表示在粒子位置Xi所表示的广播树中当节点v成为节点u的孩子节点后节点u的传输功率.令exl(Xi,u,v)表示在粒子位置Xi所表示的广播树中当节点v成为节点u的孩子节点后节点u的生命期.在粒子进行搜索的过程中,可能会出现较差的粒子位置,这些较差的粒子位置不仅不会促进全局极值的进化还会增加计算时间.因此,在更新粒子位置的过程中,对新粒子位置进行一定的限制,如果新粒子位置xi,d(t+1)对应的节点Ωd[xi,d(t+1)]满足exl(Xi(t+1),Ωd[xi,d(t+1)], vtx(d))≥η,则新粒子位置xi,d(t+1)才可能有效,否则xi,d(t+1)=xi,d(t).η为预先设定的某个阈值.对粒子位置按四舍五入取整.如果粒子位置Xi发生变化,就返回true表示更新成功,否则返回false表示更新失败.更新粒子位置Xi的VaryX算法如下: ①Xi(t+1)←Xi(t);Z←{1, 2, …,N-1}, change←false. ② 如果Z=∅,转步骤⑥. ③ 从Z中随机选择一个维度d,Z←Z-{d};按式(2)计算xi,d(t+1),当xi,d(t+1)越界时使用阻尼墙[14-15]进行处理,xi,d(t+1) ←xi,d(t+1)+0.5;如果xi,d(t+1)=xi,d(t),转步骤②. ⑤xi,d(t+1)←xi,d(t),转步骤②. ⑥ 返回Xi(t+1)和change. 文献[4]的MLR-MD算法是对已有的一棵多播树进行局部优化.首先将多播树中各节点按生命期升序排列,然后按此顺序对各节点进行处理.在处理每个传输节点u时,按照其波束边界节点对应的生命期增益递减的顺序依次处理其各个波束边界节点,u的波束边界节点v对应的生命期增益为节点u在移除孩子节点v后的生命期增加量.在某个节点的生命期得到提高后重新对多播树中的各节点按生命期进行升序排列,并开始新的循环.在使用MLR-MD算法局部优化广播树时,由于广播树包含了所有网络节点,因此不存在使用树外节点调整树结构的情况.在迭代更新粒子位置的过程中使用简化的MLR-MD(simplified MLR-MD, SMLR-MD)对粒子位置进行局部优化,SMLR-MD在每轮循环中只对最小生命期节点进行处理,以减少计算时间. 当搜索状态较差时需要新增粒子以提高全局极值发生进化的可能性.文献[16]指出,在新增粒子时通过交叉组合随机选择的2个粒子的个体极值点,可以构造出较好的粒子初始位置,从而有利于全局极值的进化.若粒子数M=1,即当前只有1个粒子,假设该粒子为i,则新粒子k的位置Xk取为粒子i的个体极值点Yi;若粒子数M>1,首先随机选择2个粒子,然后对它们的个体极值点进行交叉组合来构造新粒子k的位置Xk. 假设被随机选择用来交叉组合个体极值点的2个粒子为i和j,令E(Yi)表示粒子i的个体极值点Yi所表示的广播树的边集,E(Yj)表示粒子j的个体极值点Yj所表示的广播树的边集,在E(Yi)和E(Yj)的基础上使用DMMT-DA-NC算法构造新粒子k的位置Xk.DMMT-DA-NC是从源节点开始自上而下地构造广播树,对于构造过程中的每次迭代,如果E(Yi)∪E(Yj)中存在连接中间树(已形成的部分树)内的节点到中间树外的节点的边,则使用这些边进行构造,否则,使用E(Yi)∪E(Yj)以外的边进行构造. 在初始化新粒子k的位置Xk之后,新粒子k的个体极值点Yk初始化为Xk.随机初始化新粒子k的速度为Vk. 设粒子群共包含Minit个初始粒子.贪心初始化粒子位置可以加快收敛速度[22],在算法的初始化阶段,对每个粒子的位置使用DMMT-DA-NC算法[10]进行构造并使用MLR-MD算法[4]进行局部优化,这样可使得粒子从一个较好的位置开始进行搜索,MLBPSO算法从一个较好的解开始.令δ表示总迭代次数.MLBPSO算法是基于使用了阻尼边界条件[14-15]、EPUS-PSO[16]的粒子群体管理和解信息共享策略的粒子群优化,并使用MLR-MD局部优化粒子位置以及使用DMMT-DA-NC构造粒子的初始位置.求解最大生命期广播树的MLBPSO算法如下: ② 更新惯性权重w,evol←false,i←1. ③ 按式(3)更新粒子i的速度Vi;使用VaryX算法更新粒子i的位置Xi,如果Xi更新失败,转步骤⑦. ④ 使用SMLR-MD算法对Xi进行局部优化;计算粒子i的适应度值fit(Xi);如果fit(Xi)>fit(Yi),Yi←Xi,否则,转步骤⑦. ⑤ 如果i=b,evol←true,转步骤⑦. ⑥ 如果fit(Yi)>fit(Yb),evol←true,b←i. ⑦i←i+1;如果i≤M,转步骤③. ⑧λ←λ+1;如果evol=true,μ←0,impr←true,转步骤⑩. ⑨μ←μ+1;如果M≥Mmax,转步骤. ⑩ 如果λ<λmax,转步骤;如果impr=false或者M≤1,转步骤. 令A1表示DMMT-DA-NC算法,A2表示DMMT-DA-NC+MLR-MD算法,A3表示MLBPSO算法.实验结果如表1~表4所示,其中对A2的广播生命期比A1的平均提高率、A3的广播生命期比A1及A2的平均提高率进行了统计.由实验结果可知,MLBPSO算法的计算结果优于DMMT-DA-NC算法和DMMT-DA-NC+MLR-MD算法.MLBPSO是基于群体迭代寻优因而运行时间长于DMMT-DA-NC和DMMT-DA-NC+MLR-MD. MLBPSO较DMMT-DA-NC和DMMT-DA-NC+MLR-MD的平均提高率在θmin=π/3时比在θmin=π/12时低.这是由于θmin越大,节点波束宽度可优化的空间越小,问题可优化的空间越小,DMMT-DA-NC求得的解越接近于最优解(当θmin=2π即为全向天线时,DMMT-DA-NC求得的解为最优解),相应地MLBPSO较DMMT-DA-NC和DMMT-DA-NC+MLR-MD的平均提高率会降低. 网络规模越大,MLBPSO的运行时间越长,这是因为网络规模越大,维数D就越大,平均可以传输到达每个节点的其他节点越多. 表1 当时的实验结果 表2 当时的实验结果 表3 当时的实验结果 表4 当时的实验结果 在无线自组网中,能量受限的特性制约着网络的生命期.本文针对在使用单波束定向天线时的最大生命期广播路由问题,提出了一个构造最大生命期广播树的粒子群算法MLBPSO.该算法在计算过程中动态地调整粒子群体、增强粒子间解信息交流、使用阻尼墙处理粒子越界,粒子在已有搜索经验的指导下随机地变换广播树结构,以尽可能搜索到最优的最大生命期广播树.同时,MLBPSO算法结合MLR-MD算法对粒子位置进行局部优化,结合DMMT-DA-NC算法构造粒子的初始位置,以提高求解效率.由于MLBPSO能够搜索出更优的广播树结构,因而可以更有效地提高广播生命期. ) [1]李政,李德英. 无线自组织网络中能量有效的广播与组播[J]. 软件学报,2010,21(8): 2023-2036. Li Zheng, Li Deying. Energy-efficient broadcast and multicast in wireless ad hoc networks [J].JournalofSoftware, 2010,21(8): 2023-2036. (in Chinese) [2]Das A K, Marks R J, El-Sharkawi M, et al. MDLT: a polynomial time optimal algorithm for maximization of time-to-first-failure in energy constrained wireless broadcast networks [C]//ProceedingsoftheIEEEGlobalTelecommunicationsConference. San Francisco, California, USA, 2003: 362-366. [3]Kang I, Poovendran R. Maximizing static network lifetime of wireless broadcast ad hoc networks [C]//ProceedingsoftheIEEEInternationalConferenceonCommunications. Anchorage, Alaska, USA, 2003: 2256-2261. [4]Hou Y T, Shi Y, Sherali H D, et al. Multicast communications in ad hoc networks using directional antennas: a lifetime-centric approach [J].IEEETransactionsonVehicularTechnology, 2007,56(3): 1333-1344. [5]Wieselthier J E, Nguyen G D, Ephremides A. Energy-aware wireless networking with directional antennas: the case of session-based broadcasting and multicasting [J].IEEETransactionsonMobileComputing, 2002,1(3): 176-191. [6]Guo S, Yang O. Formulation of optimal tree construction for maximum lifetime multicasting in wireless ad-hoc networks with adaptive antennas [C]//ProceedingsoftheIEEEInternationalConferenceonCommunications. Seoul, Korea, 2005: 3370-3374. [7]Guo S, Yang O. Multicast lifetime maximization for energy-constrained wireless ad-hoc networks with directional antennas [C]//ProceedingsoftheIEEEGlobalTelecommunicationsConference. Dallas, Texas, USA, 2004: 4120-4124. [8]Guo S, Leung V C M, Yang O W W. Distributed multicast algorithms for lifetime maximization in wireless ad hoc networks with omni-directional and directional antennas [C]//ProceedingsoftheIEEEGlobalTelecommunicationsConference. San Francisco, California, USA, 2006: 4151642. [9]Guo S, Yang O, Leung V. Approximation algorithms for longest-lived directional multicast communications in WANETs [C]//Proceedingsofthe8thACMInternationalSymposiumonMobileAdHocNetworkingandComputing. Montreal, Quebec, Canada, 2007: 190-198. [10]Guo S, Leung V, Jiang X. Distributed approximation algorithms for longest-lived multicast in WANETs with directional antennas [J].IEEETransactionsonWirelessCommunications, 2010,9(7): 2227-2237. [11]朱晓建,沈军. 基于粒子群优化的ad hoc网络最小能耗多播路由算法[J]. 通信学报,2012,33(3):52-58. Zhu Xiaojian, Shen Jun. Minimum energy consumption multicast routing in ad hoc networks based on particle swarm optimization [J].JournalonCommunications, 2012,33(3): 52-58. (in Chinese) [12]Hsiao P C, Chiang T C, Fu L C. Particle swarm optimization for the minimum energy broadcast problem in wireless ad-hoc networks [C]//ProceedingsoftheIEEECongressonEvolutionaryComputation. Brisbane, Australia, 2012: 6252949. [13]王楷. 基于粒子群优化的Ad Hoc网络多播路由研究[D]. 武汉:华中师范大学计算机科学系,2007. [14]Huang T, Mohan A S. A hybrid boundary condition for robust particle swarm optimization [J].IEEEAntennasandWirelessPropagationLetters, 2005,4: 112-117. [15]Xu S, Rahmat-Samii Y. Boundary conditions in particle swarm optimization revisited [J].IEEETransactionsonAntennasandPropagation, 2007,55(3): 760-765. [16]Hsieh S T, Sun T Y, Liu C C, et al. Efficient population utilization strategy for particle swarm optimizer [J].IEEETransactionsonSystems,Man,andCybernetics—PartB:Cybernetics, 2009,39(2): 444-456. [17]Kennedy J, Eberhart R. Particle swarm optimization [C]//ProceedingsoftheIEEEInternationalConferenceonNeuralNetworks. Perth, Australia, 1995: 1942-1948. [18]Eberhart R, Kennedy J. A new optimizer using particle swarm theory [C]//ProceedingsoftheSixthInternationalSymposiumonMicroMachineandHumanScience. Nagoya, Japan, 1995: 39-43. [19]Robinson J, Rahmat-Samii Y. Particle swarm optimization in electromagnetics [J].IEEETransactionsonAntennasandPropagation, 2004,52(2): 397-407. [20]Shi Y, Eberhart R. A modified particle swarm optimizer [C]//ProceedingsoftheIEEEInternationalConferenceonEvolutionaryComputation. Anchorage, Alaska, USA, 1998: 69-73. [21]Salman A, Ahmad I, Al-Madani S. Particle swarm optimization for task assignment problem [J].MicroprocessorsandMicrosystems, 2002,26(8): 363-371. [22]Liu X, Su J, Han Y. An improved particle swarm optimization for traveling salesman problem [C]//Proceedingsofthe3rdInternationalConferenceonIntelligentComputing. Qingdao, China, 2007: 803-812.
c2rand()(yk,d(t)-xi,d(t))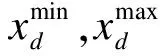
3 最大生命期广播树的粒子群算法构造
3.1 粒子定义

3.2 粒子位置更新

3.3 粒子位置局部优化
3.4 新增粒子构造
3.5 MLBPSO算法描述

4 仿真结果

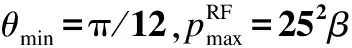
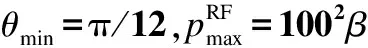

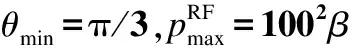
5 结语

