基于一维PCA-EIR技术的二维SVD-FIR滤波器设计
王 浩 包永强 奚 吉 赵 力 邹采荣
(1东南大学水声信号处理教育部重点实验室,南京 210096)
(2南京工程学院通信工程学院,南京 210093)
1D和2D数字滤波器在数字信号处理领域具有重要且广泛的应用.根据冲击响应的性质,1D和2D数字滤波器可分为1D和2D有限冲击响应(FIR)滤波器以及1D和2D无限冲击响应(IIR)滤波器.FIR数字滤波器具有严格的线性相位响应以及稳定的系统响应,是数字滤波器研究及应用领域的重要组成部分.然而,在相同的幅度频率响应指标前提下,与IIR数字滤波器相比,FIR数字滤波器的阶数较高,故其延时和硬件执行复杂度(用乘法器和加法器个数来衡量)也较高.当数字滤波器过渡带较窄时,FIR数字滤波器硬件执行复杂度高的问题尤其突出.为减少1D FIR数字滤波器的硬件执行复杂度,Neuvo等[1]提出了一种内插有限冲击响应滤波器设计方法;Lim等提出了1D屏罩法[2]和1D外插法[3-7].其中,1D外插法利用1D低通或高通FIR数字滤波器系数的类周期性来降低滤波器的硬件执行复杂度.为了减少2D FIR数字滤波器[8-9]的硬件执行复杂度,Mersereau等[10]提出了一种基于McClellan变换的2D FIR数字滤波器设计方法;Lim等[11]提出了2D屏罩法;Trettel 等[12-15]提出了一种基于奇异值分解(SVD)的2D FIR(2D SVD-FIR)数字滤波器设计方法;Lu等[16]提出了一种基于系数稀疏的低复杂度2D FIR滤波器设计方法.2D SVD-FIR数字滤波器由若干2D FIR子滤波器并联构成,每一个2D FIR子滤波器由2个1D FIR子滤波器串联构成[13].
本文基于1D EIR技术合成了2D SVD-FIR数字滤波器的所有1D FIR子滤波器.仿真结果表明,该方法可以有效降低2D FIR数字滤波器的硬件执行复杂度.
1 1D EIR滤波器设计


(1)
由于类周期性,一般能找到3个正整数M,d,R,使得以下的近似关系成立:
h1≈α1h0,h2≈α2h0, …,hR≈αRh0
式中,h0为基向量;α1,α2,…,αR为尺度因子,可以通过线性规划的方法获得.上述近似关系即为原始1D EIR技术的基本原理.以此为基础,原型1D FIR 数字滤波器可采用Zhou等[5]提出的1D EIR滤波器结构近似实现.为改进原始1D EIR技术的性能,Yu等[4]提出了一种基于半无限规划(SIP)的1D EIR(1D SIP-EIR)技术,即采用SIP技术对原始1D EIR滤波器设计中的未知参数进行联合优化.然而,SIP技术是一种非线性规划,其设计执行需要一个较好的迭代初值,该初值一般通过其他1D EIR滤波器设计技术获得.因此,1D SIP-EIR技术并非一种独立的1D EIR技术.基于主分量(PCA)分析的1D EIR(1D PCA-EIR)技术[5-6]是一种独立且效果较好的1D EIR 技术.该技术通过选用矩阵HHT的若干最大特征向量,对矩阵H中的每一列向量进行线性近似.Wang等[6]提出了一种可以获得分析解的方法以减弱1D PCA-EIR数字滤波器的量化效应.此外,Yu等[7]对如何设计具有离散系数的1D EIR滤波器进行了研究.本文仅考虑具有连续系数的1D EIR滤波器设计.
2 基于SVD的2D FIR滤波器设计
线性相位2D FIR滤波器可由其冲击响应矩阵或者频率响应矩阵来表示.本文仅考虑冲击响应为实数的2D FIR数字滤波器,而且在无额外说明的情况下均假定2D FIR数字滤波器具有严格的线性相位.设Φ为一个L1×W1的矩阵,表示任一实系数2D FIR 数字滤波器的冲击响应;Ω为一个L2×W2的矩阵,表示任一实系数2D FIR数字滤波器的理想零相位频率响应.分别对矩阵Φ和Ω进行奇异值分解可得
式中,U1,V1,U2,V2均为正交矩阵;S1和S2为对角矩阵.这些矩阵均无明确的物理含义,都是由滤波器系数矩阵Φ和频率响应矩阵Ω推导得到.
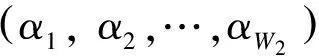
式中,u1k,v1k,u2k,v2k分别为矩阵U1,V1,U2,V2的第k个列向量.设矩阵Φ,Ω的秩分别为r1和r2,则K1≤r1,K2≤r2.u1k,v1k(k=1,2,…,r1)分别为同时镜像对称或反对称;u2k,v2k(k=1,2,…,r2)亦分别为同时镜像对称或反对称.如果K1=r1(或者K2=r2),那么Φ(或者Ω)可以被这些1D列向量零误差表示.对2D FIR数字滤波器的冲击响应矩阵Φ进行SVD操作时,可令u1k和v1k(k=1,2,…,K1)为1D FIR滤波器的冲击响应序列.对2D FIR 数字滤波器的频率响应矩阵Ω进行SVD操作时,可令u2k和v2k(k=1,2,…,K2) 为1D FIR数字滤波器的频率响应序列.利用SVD技术,由矩阵Φ(或者Ω)表示的2D FIR 滤波器可以通过K1(或者K2)个2D FIR子滤波器并联在一起取和实现或者近似实现,其中每一个2D FIR子滤波器由2个1D FIR子滤波器串联构成.
3 1D FIR子滤波器合成
设ρ(n)为2D SVD-FIR数字滤波器中的某一个1D FIR子滤波器的系数,2l+1为子滤波器的阶数或长度.利用1D PCA-EIR 技术合成这类1D FIR子滤波器的步骤如下:
① 选取参数M,d,R,将滤波器系数ρ(n)(M+1≤n≤1)组成矩阵,即
② 采用1D PCA-EIR技术合成由ρ(n)表示的1D FIR子滤波器,即选取矩阵ρρT的p个最大特征向量,对矩阵ρ中的每一个列向量进行线性近似.
③ 计算合成后的1D FIR子滤波器的频率响应,并与原型1D FIR子滤波器的频率响应进行比较.二者的差值为频率范围内的最大绝对误差.若二者的差值在一个很小范围内,且1D EIR子滤波器的执行复杂度小于原型1D FIR子滤波器,则1D EIR子滤波器可替代原型1D FIR子滤波器.否则,原型1D FIR子滤波器保持不变.参数ε表示原型子滤波器与合成子滤波器的频率域差值,该参数直接影响合成的2D SVD-FIR滤波器的通带波纹和阻带衰减.
在实际滤波器设计中,参数ε一般通过尝试获取,即先设定ε为某一值,然后计算所合成的2D SVD-FIR滤波器的通带波纹和阻带衰减参数.若合成滤波器的通带波纹参数和阻带衰减参数满足滤波器的设计要求,则设计结束;否则,减小ε的取值(ε越小,说明原型1D子滤波器与合成的1D EIR子滤波器越接近),直到滤波器的通带波纹和阻带衰减满足设计要求.在给定参数M,d,R的情况下,参数p可通过完整搜索来获得最优取值.该最优值既可满足通带波纹和阻带衰减参数的指标要求,又能使所设计滤波器的复杂度最小.本文基于1D PCA-EIR技术合成了2D SVD-FIR滤波器中的1D FIR子滤波器,其基本原理是利用PCA技术对子滤波器系数矩阵ρ进行降维.需要指出的是,在以往文献中,1D EIR技术主要用于设计低通或高通FIR数字滤波器,而本文中需要合成的FIR子滤波器是任意的FIR滤波器.
4 仿真
下面通过2个设计实例来验证所提方法的有效性.
设计实例1假定需要设计的2D FIR椭圆低通滤波器的理想频率响应为
(2)
式中,ap,bp分别表示滤波器频域水平和垂直方向上的通带截止角频率;as,bs分别表示滤波器频域水平方向和垂直方向上的阻带截止角频率;ω1,ω2分别表示滤波器频域水平方向和垂直方向上的角频率.此处,ap=0.31π;bp=0.56π;as=0.51π;bs=0.76π.所期望的通带和阻带最大波纹均为-30 dB.
设计实例2假定需要设计的2D FIR椭圆带通滤波器的理想频率响应为
(3)
式中,ap1,ap2表示带通滤波器频域水平方向上的通带截止角频率;bp1,bp2表示带通滤波器频域垂直方向上的通带截止角频率;as1,as1表示带通滤波器频域水平方向上的阻带截止角频率;bs1,bs2表示带通滤波器频域垂直方向上的阻带截止角频率.此处,ap1=0.31π;bp1=0.56π;ap2=0.51π;bp2=0.76π;as1=0.11π;bs1=0.36π;as2=0.71π;bs2=0.96π.所期望的通带和阻带最大波纹均为-20 dB.
下面分别采用窗函数法、冲击响应矩阵SVD法、频率响应矩阵SVD法来设计满足以上指标要求的2D FIR数字滤波器,并采用1D PCA-EIR技术合成2D SVD-FIR 数字滤波器中的所有1D FIR子滤波器.
针对设计实例1和2,采用上述5种方法设计的2D FIR数字滤波器的性能指标分别见表1和表2.从表1中可以看出,对于设计实例1,5种方法所设计的滤波器通带波纹和阻带衰减均达到-30 dB.方法4较之方法2能节约13.16%(25个)的乘法器和17.58%(64个)的加法器;方法5较之方法3能节约7.37%(14个)的乘法器和13.19%(48个)的加法器.从表2中可以看出,对于设计实例2,5种方法所设计的滤波器通带波纹和阻带衰减均达到-20 dB.方法4较之方法2可节约8.85%(17个)的乘法器和13.15%(48个)的加法器;方法5较之方法3可节约8.13%(13个)的乘法器和14.47%(44个)的加法器.此外,在设计实例1中,方法2设计的2D SVD-FIR数字滤波器具有5个并行结构(对于2D SVD-FIR数字滤波器而言,每个并行结构由2个1D FIR子滤波器级联,故此处共10个1D FIR子滤波器).采用方法3对设计实例1中的10个子滤波器进行外插时,参数M,p,d,R的取值情况见表3.针对设计实例1,采用方法4设计的2D FIR数字滤波器的幅度响应见图1(a);针对设计实例2,采用方法5设计的2D FIR数字滤波器的幅度响应见图1(b).

表1 椭圆低通滤波器的性能指标

表2 椭圆带通滤波器的性能指标

表3 基于方法3设计的2D SVD-FIR滤波器参数

图1 2D SVD-FIR数字滤波器的频率响应
5 结语
本文基于1D PCA-EIR技术设计合成了2D SVD-FIR 数字滤波器中的1D FIR 子滤波器.仿真结果表明,在2D SVD-FIR数字滤波器频率响应性能未受影响的前提下,采用1D PCA-EIR 技术设计2D SVD-FIR 数字滤波器中的1D FIR子滤波器,较之传统的2D SVD-FIR数字滤波器设计,可以减少硬件执行所需的乘法器数目和加法器数目,从而验证了本文方法的有效性.由此可知,1D EIR技术可用于合成任意1D FIR数字滤波器.
)
[1]Neuvo Y, Dong C Y, Mitra S K. Interpolated finite impulse response filters [J].IEEETransactionsonAcoustics,Speech,andSignalProcessing, 1984,32(3): 563-570.
[2]Lim Y C, Yu Y J, Teo K L, et al. FRM-based FIR filters with optimum finite word-length performance [J].IEEETransactionsonSignalProcessing, 2007,55(6): 2914-2924.
[3]Lim Y C, Liu B. Extrapolated impulse response FIR filter [J].IEEETransactionsonCircuitsandSystems, 1990,37(12): 1548-1551.
[4]Yu Y J, Zhao G H, Teo K L, et al. Optimization of extrapolated impulse response filters using semi-infinite programming [C]//ProceedingsoftheFirstInternationalSymposiumonControl,CommunicationsandSignalProcessing. Hammamet, Tunisia, 2004: 397-400.
[5]Zhou L H, Pei W J, Xi P C, et al. Extrapolated impulse filter using coefficient-auto-correlation matrix decomposition [J].SignalProcessing, 2008,88(7): 1762-1774.
[6]Wang H, Zhao L, Wang H, et al. An optimal design of the extrapolated impulse response filter with analytical solutions [J].SignalProcessing, 2012,92(7): 1665-1672.
[7]Yu Y J, Shi D, Lim Y C. Design of extrapolated impulse response filter with residual compensation in subexpression space [J].IEEETransactionsonCircuitsandSystems, 2009,56(12): 2621-2633.
[8]Huang T S. Two-dimensional windows [J].IEEETransactionsonAudioandElectroacoustics, 1972,20(1): 88-89.
[9]Kockanat S, Karaboga N, Koza T. Image denoising with 2D FIR filter by using artificial bee colony algorithm [C]//2012InternationalSymposiumonInnovationsinIntelligentSystemsandApplications(INISTA). Trabzon, Turkey, 2012: 1-4.
[10]Mersereau R, Mecklenbrauker W, Quatieri T J. McClellan transformations for two-dimensional digital filtering—part Ⅰ: design [J].IEEETransactionsonCircuitsandSystems, 1976,23(7): 405-414.
[11]Lim Y C, Lian Y. The optimal design of one-and two-dimensional FIR filters using frequency response making technique [J].IEEETransactionsonCircuitsandSystems, 1993,40(2): 88-95.
[12]Trettel S, Shanks J L. The design of multistage separable planar filters [J].IEEETransactionsonGeoscienceandElectronics, 1971,9(1): 10-27.
[13]Lu W S, Wang H P, Antoniou A. Design of two-dimensional FIR digital filters by using the singular-value decomposition [J].IEEETransactionsonCircuitsandSystems, 1990,37(1): 35-46.
[14]Zhu W P, Ahmad M O, Swamy M N S. Realization of 2D linear-phase FIR filters by using the singular-value decomposition [J].IEEETransactionsonSignalProcessing, 1999,47(5): 1349-1358.
[15]Elkarami B, Ahmadi M. An efficient design of 2D FIR digital filters by using singular value decomposition and genetic algorithm with canonical signed digit (CSD) coefficients [C]//Proceedingsofthe54thInternationalMidwestSymposiumonCircuitsandSystems(MWSCAS). Seoul, South Korea, 2011: 1-4.
[16]Lu W S, Hinamoto T. Two dimensional digital filters with sparse coefficients [J].MultidimensionalSystemandSignalProcessing, 2010,22(1/2/3): 173-189.

