波形未知的水声脉冲信号双阵元相关匹配场定位

李 焜 方世良 安 良

(东南大学水声信号处理教育部重点实验室, 南京 210096)

确定水下声源的位置是水声信号处理中的一个关键问题．考虑到水声环境的复杂性,为了能够更准确地对水下目标实施定位,多数文献[1-6]从声传播的角度出发,使用匹配场定位技术来确定声源的位置．传统的匹配场定位技术一般多采用阵列的处理方式,具有大的孔径,以获得良好的阵增益和分辨性能．但是采用多阵元的大阵列,一方面增加了系统的开销,给基阵的设计带来不便;另一方面,在实际海水中布放时会受到诸如阵倾斜以及阵元失效等影响,增加了对水下目标定位的难度．此外,在某些应用方面,由于受到安装平台尺寸的限制,也使得多阵元的布放无法实现．因此,采用较少的阵元个数来确定水下目标的位置已被研究人员所关注[7-15]．

本文研究利用双阵元来对波形未知的水声脉冲信号进行声源定位的方法．首先在时域建立水听器接收信号模型,采用最小二乘的方法获得发射声源的估计值并产生出拷贝场信号,然后通过对双阵元接收信号与拷贝场信号的互相关函数进行匹配处理来构造表征目标位置的模糊表面,从而确定目标声源的位置．

1 信号模型

位于海洋环境中(r0,z0)位置处的发射信号经过海洋波导传播后,两垂直接收阵元所接收到的信号可表示为如下卷积的形式:

(1)

式中,s(t)为发射信号;hj(t)为海洋信道脉冲响应;nj(t)为噪声．在离散时间情形下,可将式(1)表示为时域卷积和的形式：

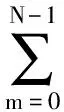
(2)

将式(2)写为矩阵运算形式,则有

yj=Hjs+nj

(3)

其中

s=[s(0)s(1) …s(N-1)]T

yj=[yj(0)yj(1) …yj(2N-2)]T

nj=[nj(0)nj(1) …nj(2N-2)]T

2 定位原理

2.1 算法描述

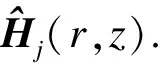
利用最小二乘的方法构造如下误差函数:

(4)

对式(4)中s进行求导,并令导数为0,就可得到每个网格点上发射信号的估计值:

(5)

(6)

搜索定位函数的最大值,从而确定目标位置,即

(7)

2.2 算法分析

为便于表述,将2路水听器接收的信号写为

yj=Hjs+nj=xj+njj=1,2

(8)

相应地将拷贝场信号表示为

(9)

则双阵元2路接收信号之间的互相关ρ12为

ρ12=y1(n)⊙y2(n)=
(x1(n)+n1(n))(x2(n)+n2(n))=
x1(n)⊙x2(n)+x1(n)⊙n2(n)+
n1(n)⊙x2(n)+n1(n)⊙n2(n)

(10)

式中,⊙表示相关运算．

假设x1与n2、x2与n1以及n1与n2之间互不相关,则可将式(10)表示为

(11)

式中,W2为由x2构成的矩阵．

m=-2N+2,-2N+1,…,2N-2

(12)

则误差函数为

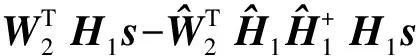
(13)

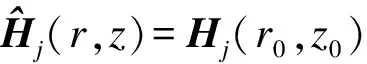
(14)

(15)

3 数值仿真

为说明本方法更具一般性,分别采用2种声场传播模型对2种常见的水声脉冲信号进行仿真实验．脉冲信号类型选为CW脉冲信号和LFM脉冲信号．CW信号的频率为250Hz,脉冲宽度为0.1s,LFM信号的频率范围为150～350Hz,脉冲宽度为0.05s．目标位于水下60m,2个接收水听器分别位于水下50m和70m,源与接收机之间的距离设为5km．仿真所用的海洋环境参数为:海水深度为110m,海水密度为ρw=1g/cm3,声速剖面如图1所示,海底密度为ρb=1.9g/cm3,海底声速cb=1700m/s,衰减系数为0.5λdB-1．对于CW信号采用射线模型求解声线的到达结构,产生信道脉冲响应;对于LFM信号使用简正波模型计算声源信号每个频率分量在水听器处激励的声场,得到频域亥姆霍兹方程的解,再反变换回时域求得时域波动方程的解,产生相应的信道脉冲响应．

模拟水听器上的接收信号为声源位置处的发射信号在接收水听器上的响应,并叠加高斯白噪声,SNR=20dB,单一水听器上的接收信号如图2所示．

图1 仿真所用的声速剖面

图2 单一水听器接收到的2种脉冲信号

在进行目标位置确定时,声源搜索范围为距离2～7km(步距100m),深度5～105m(步距2.5m),使用本方法求出相应的定位模糊表面,结果如图3(a)和图4(a)所示．对于双阵元理论上可以采用垂直水听器阵列的方式进行匹配场定位,为了进行比较,图3(b)和图4(b)给出了使用常规Bartlett匹配场处理器的双阵元匹配场定位效果．从结果可看出,本文提出的相关匹配场处理器给出的定位结果正确地反映了目标所在位置,模糊表面的峰值较为清晰;而常规的Bartlett匹配场处理器,由于阵元个数过少导致定位模糊表面的旁瓣过高,无法对目标实施精确定位．

图3 LFM脉冲信号的定位结果

图5和图6分别给出了LFM脉冲信号和CW脉冲信号的模糊表面在估计位置处的距离和深度切片．图中距离估计的主瓣控制区δrange=500m,深度估计的主瓣控制区δdepth=10m,σn表示旁瓣级的标准差．从图中可以看出,双阵元相关匹配场处理器具有较高的峰值旁瓣比．

4 结语

采用较少的阵元个数对水下目标实施定位一直是国内外研究的热点和难点．本文以水声脉冲信号的定位作为切入点,研究利用双水听器在未知脉冲信号波形下的匹配场定位．采用时域最小二乘解的方法获得搜索区域每个网格点发射信号的估计值,由此产生出拷贝场信号;通过计算双阵元接收信号的互相关与拷贝场信号的互相关之间的误差函数,借助矩阵广义逆的性质,寻找接收信号与拷贝场信号之间的最优匹配来确定目标声源的位置．数值仿真结果显示,本方法不受信号形式和声场传播模型的限制,克服了传统匹配场处理由于阵元个数过少而导致定位模糊表面旁瓣过高的问题,具有较好的定位效果．实际中,由于受海洋环境不确定性的影响,对于失配环境下本方法的稳健性还有待进一步研究．

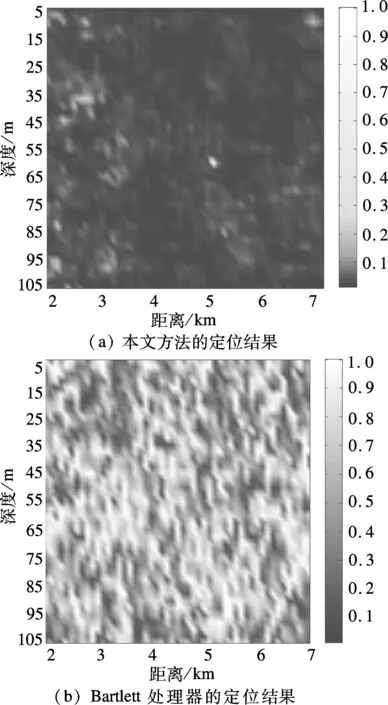
图4 CW脉冲信号的定位结果

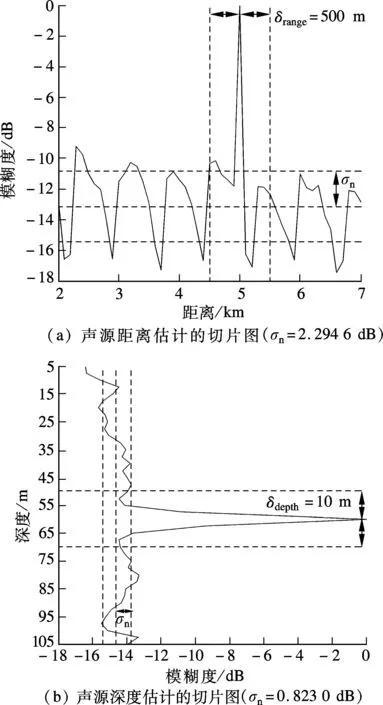
图5 LFM脉冲信号相关匹配场处理器的模糊度函数切片图

图6 CW脉冲信号相关匹配场处理器的模糊度函数切片图

)

[1]Xiao Z, Xu W, Gong X Y. Robust matched field processing for source localization using convex optimization[C]//IEEEOceans’2009ConferenceProceedings. Bremen, Germany, 2009: 5278253.

[2]Kim K, Seong W, Lee K. Adaptive surface interference suppression for matched-mode source localization[J].IEEEJournalofOceanEngineering, 2010,35(1): 120-130.

[3]Wang Q, Jiang Q. Simulation of matched field processing localization based on empirical mode decomposition and Karhunen-Loève expansion in underwater waveguide environment[J].EURASIPJournalonAdvancesinSignalProcessing, 2010,2010: 483524.

[4]Wu K M, Ling Q, Wu L X. Positioning ability comparison research on several matched-field processing methods with increasing white noise[C]//2011IEEEInternationalConferenceonSignalProcessing,CommunicationsandComputing. Xi’an, China, 2011: 6061678.

[5]Lin W S, Liang G L, Wang Y, et al. Source localization with acoustic intensity flux matched-field processing [C]//2011InternationalConferenceonWirelessCommunicationsandSignalProcessing. Nanjing, China, 2011: 6096927.

[6]Xu W, Xiao Z, Yu L. Performance analysis of matched-field source localization under spatially correlated noise field [J].IEEEJournalofOceanEngineering, 2011,36(2):273-284.

[7]Frazer L N, Pecholcs P I. Single-hydrophone localization[J].JournalofAcousticalSocietyofAmerica, 1990,88(2): 995-1002.

[8]Lee Y P. Time-domain single hydrophone localization in a real shallow water environment[C]//IEEEOceans’1998ConferenceProceedings. Nice, France, 1998: 1074-1077.

[9]Jesus S M, Porter M B, Stéphan Y, et al. Single hydrophone source localization[J].IEEEJournalofOceanEngineering, 2000,25(3):337-346.

[10]Touzé G L, Torras J, Nicolas B, et al. Source localization on a single hydrophone[C]//IEEEOceans’2008ConferenceProceedings. Quebec City, Canada, 2008: 5151936.

[11]Jemmott C W, Culver R L, Bose N K. Passive sonar target localization using a histogram filter with model-derived priors[C]//IEEEConferenceonSignal,SystemsandComputers. Pacific Grove, USA, 2008: 283-287.

[12]Chapin S R. Application of the method of least squares to a solution of the matched field localization problem with a single hydrophone[D]. New Orleans,LA,USA: The University of New Orleans, 2008.

[13]Tao H L, Hickman G, Krolik J L, et al. Single hydrophone passive localization of transiting acoustic sources[C]//IEEEOceans’ 2007ConferenceProceedings. Aberdeen, Scotland, 2007: 4302377.

[14]Tiemann C O, Thode A M, Straley J, et al. Three-dimension localization of sperm whales using a single hydrophone[J].JournalofAcousticalSocietyofAmerica, 2006,120(4): 2355-2365.

[15]Skarsoulis E K, Kalogerakis M A. Two-hydrophone localization of a click source in the presence of refraction[J].AppliedAcoustics, 2006,67(11): 1202-1212.