基于干扰保护的同信道干扰下VHT WLANs性能
冀保峰 杨绿溪
(东南大学信息科学与工程学院,南京210096)
随着Internet的迅速发展,信息获取的及时性和便利性显得尤为重要,无线局域网(WLAN)的灵活性、拓展性、移动性以及简便安装等特性使得WLAN产业成为当前一个重要的发展热点.自2008年上半年起,IEEE就启动了WLAN新标准的制定工作,它的目标是使无线Wi-Fi的传输速度达到1 Gbit/s以上,为此成立了超高吞吐量(VHT) 的工作组.
VHT WLANs工作于5 GHz频段,在通道的设置上,沿用802.11n的多入多出(MIMO)通信技术,并推广到多用户MIMO通信技术(MU-MIMO),其中MU-MIMO采用MIMO-OFDM模式[1]. 美国、欧洲、中国等管制地区所允许信道最多可同时时分支持2个160 MHz信道和5个80 MHz信道,而在目前无线局域网飞速发展的今天,热点覆盖越来越多,同信道干扰十分严重,因此系统容量会因同信道干扰而严重降低.本文首先分析了同信道干扰下聚合干扰对VHT WLANs的影响,并提出了一种基于干扰保护的站点接入机制,该方案的引入使得VHT WLANs在聚合干扰的影响下仍能最大化系统的吞吐量.
关于WLAN的研究已有很多.Bianchi[2]是最早对802.11的机制DCF进行性能分析,利用二维Markov链描述了用户接入机制的CSMA,并且分析其吞吐量的性能[2].Nguyen等[3]在假定所有基本业务集(BSS)使用同一频带作为主信道的情况下对密集的802.11网络进行了性能分析,得到密集网络下最优的热点数目, 并在此基础上对802.11网络进行了几何规划,得出了服从Matern点过程下达到最优吞吐量的热点数目.Ge等[4]对同信道干扰下的多小区协作蜂窝网络进行了容量分析,推导了聚合干扰下多用户MIMO的性能.本文在分析同信道干扰下VHT WLANs性能的基础上,提出了一种基于干扰保护的站点接入机制,使得VHT WLANs能最大化系统吞吐量.
1 系统模型
如图1,所示,考虑2类节点:一类是站点(STA),即用户设备,均为单天线;其他节点均为干扰发送端,例如AP,其天线数Nt∈(1,2,…,∞)(目前VHT WLANs标准规定AP天线数最多可支持16根).由于实际中热点的概率分布主要有简单顺序抑制点过程(SSI)、泊松点过程(PPP)和Matern点过程(MPP),Win等[5]指出密集的发送站点服从泊松点过程,本文假定热点覆盖服从泊松分布,且多用户MIMO预编码采用线性迫零预编码.
设x(t)是进行多用户MIMO传输时的发送信号向量,yk(t)是第k个用户的接收信号,则yk(t)可表示为
yk(t)=hk(t)wx(t)+zk(t)
(1)
式中,zk(t)为零均值单位方差的加性复高斯噪声,且E{‖zk(t)‖2}=σ2.若迫零预编码矩阵表示为w=v(v′v)-1,则SNRk为

(2)

图1 干扰模型
迫零预编码的信噪比服从参数为n2=2(M-K+1)和n1=2K的F分布,其中M为发送端天线数,K为用户数[6],其概率密度函数为

(3)
利用文献[7]中公式可得第k个用户信噪比γ的累积分布函数(CDF)为

2F1(M+1,K;K+1;-σ2/γ)
(4)
当路径损耗系数σr=4时,聚合干扰的解析概率密度函数表达式可表示为[4]

(5)
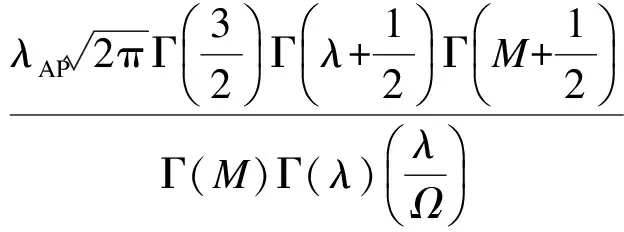

式中,σdB为分贝形式的阴影传播参数,其范围为4~9;Pr为接收端平均接收功率[8];λAP为干扰发送端密度;λ为阴影衰弱参数.
2 聚合干扰下MU-MIMO性能分析
2.1 中断概率分析
本节分析了MU-MIMO发送模式下VHT WLANs的系统性能,发送预编码矩阵采用迫零预编码,计算式如式(2)所示.聚合干扰概率密度函数采用式(5)计算,则信干比可以表示为η=Sd/SI,其中Sd为第k个用户的信号能量分布,SI为第k个用户所受的聚合干扰能量分布.由于Sd和SI是统计独立的,因此信干比η的概率密度函数可以通过下式计算:
(6)
将式(6)代入式(3)和(5),经过推导可得到信干比η的概率密度函数为

式中,P0为AP对第k个用户的发送功率;Wρ,μ(·)为Whittaker函数[9];参数ρ,μ分别为ρ=-(M+K+1/2)/2,μ=-(M-K+1/2)/2.因此η的概率密度函数可改写为
(7)

利用文献[9]中的公式可将Wρ,μ(·)表示为2个Whittaker函数之和,即

aMρ,μ(z)+bMρ,-μ(z)
式中,Φ(·,·;z)为Confluent hypergeometric函数,可级数展开为
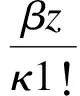
因此当发送功率较大时,用户端信干比的渐近概率密度函数表达式可以表示为

(8)
在式(8)的基础上,可以得到门限为ηth的渐近中断概率为
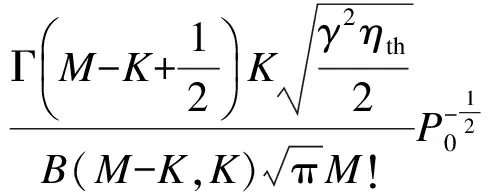
由于中断概率用分集度和阵列增益表示[10],即
Pout≃(Gc×P0)-Gd

2.2 容量分析
基本香农容量公式为
(9)
而ln(1+η)=η2F1(1,1,2,-η)[11],利用文献[11]可得
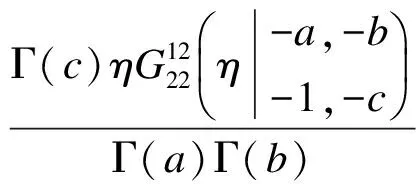
因此,第k个用户可获得的容量为
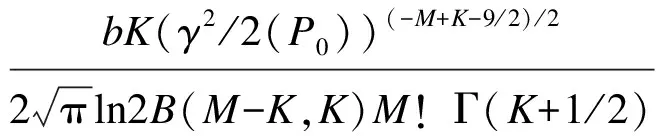

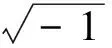
2.3 SEP分析

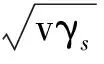
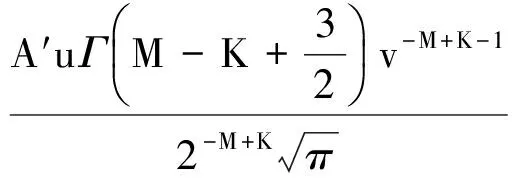
(10)
当发送端功率较大时,误符号率的渐近表达式为
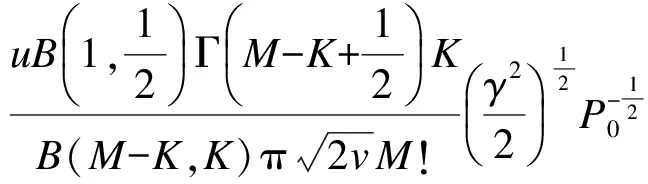
(11)
3 基于干扰保护的站点接入机制
若用Ia表示聚合干扰,则从香农容量公式(9)中可得,当存在聚合干扰时目前理论上只能获得C=(BW/2)log2(1+η)的吞吐量,若采用本文所提出的基于干扰保护的站点接入机制,则可以获得(BW/2)log2(1+SI)的吞吐量增益.下面将对该方案进行分析和验证.
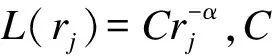
当ξj>Ithr时,站点j不允许发送;当ξj≤Ithr时,站点j允许发送,则吞吐量增益为(BW/2)log2(1+ξj).假设用户不允许j发送的区域为R2(O),该区域是以O为圆心半径为r0的圆盘状,则该模型可表示为
因此,Ij的概率密度函数可表示为

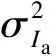
当干扰站点j的数目足够大时,由中心极限定理可知,聚合干扰Ia将服从均值为κa(1)、方差为κa(2)的高斯分布.因此由分析可知,采用基于干扰保护的站点接入机制可获得的吞吐量增益为
G=(BW/2)log2(1+ξj)
4 实验结果
热点AP的天线数为M,用户均为单天线,路径损耗系数σr=4,MU-MIMO预编码方案为迫零预编码,信道为瑞利信道.
图2给出了发送天线数M=8,用户数K=3时信干比的概率密度函数理论值和仿真结果的对比.由图可见,随着信干比的增加,概率密度函数趋于固定值.理论值与仿真值相吻合,说明本文所得的理论结果是正确的.

图2 信干比概率密度函数
图3是热点和用户之间的容量随不同发送端密度和用户数的变化情况.从图中可见,用户数K增多时,用户端获得的容量降低;发送端密度越高,容量越低.

图3 容量随着用户数K和λAP的变化
图4是平均误符号率随着不同的发送端天线数和用户数的变化情况.从图中可以看到,本文所得的渐近误符号率表达式与误符号率理论值重合.

图4 用户端平均误符号率
图5是ξj和Ij的累积分布函数.从图中可以看到,由于门限Ithr对次用户的限制导致大约27%的次用户未被允许发送,使得Ij的累积分布函数呈现为ξj的截断分布函数,并且满足FIj(Ithr)=1.
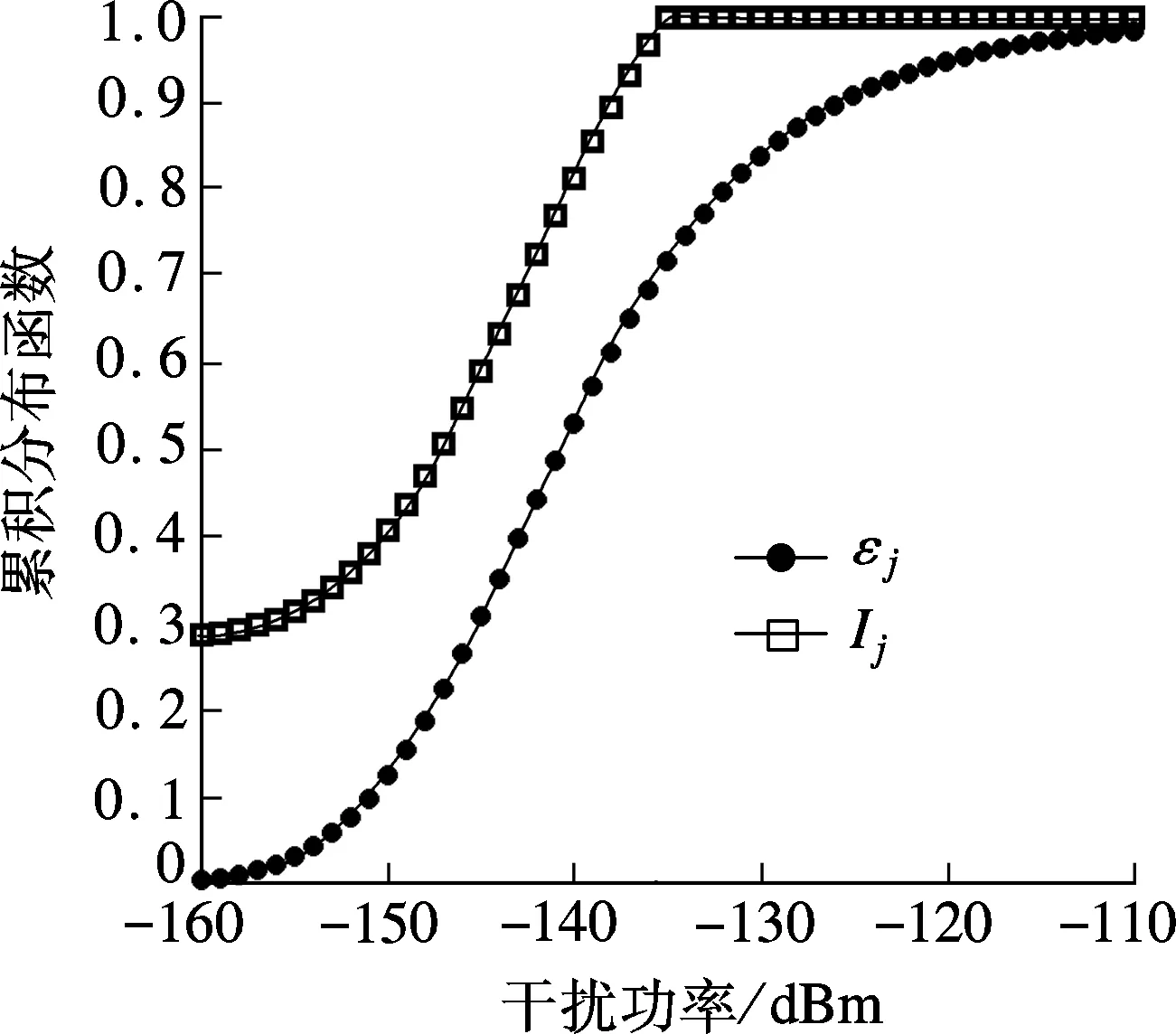
图5 所提用户选择方案和随机选择用户方案吞吐量对比
图6对比了所提方案与现有机制的吞吐量性能,其中MU-MIMO采用迫零预编码发送,N=80(0.01用户/km2);r0=4.9 km.从图中可以看到,系统吞吐量随着主用户信干比的增加而增大,这是由于主用户信干比的增加减轻了聚合干扰对它的影响,次用户可以在干扰功率小于保护门限的条件下进行数据的传输,从而增加了系统吞吐量.

图6 基于干扰保护机制与现有机制性能对比
5 结语
本文针对多热点覆盖时同信道聚合干扰的场景进行了性能分析,其中热点覆盖位置服从泊松分布,MU-MIMO采用线性预编码得到了用户信干比的闭合概率密度函数表达式,并在此基础上推导了用户信干比的累积分布函数、容量和SEP表达式;由于多热点覆盖下大量站点将竞争信道的使用权,WLAN的载波侦听机制虽能在一定程度上降低同信道的干扰,但聚合干扰的存在使得载波侦听机制不能最大化WLAN的吞吐量.本文提出了一种基于干扰保护的站点接入机制.该机制的引入使得同信道干扰下VHT WLANs能获得系统的吞吐量最大化,并且在实际中也易于实现;本文最后通过仿真验证了所提方案的正确性和有效性.
)
[1]802 Committee. IEEE 802.11ac/D2.0 Draft STANDARD for wireless LAN medium access control (MAC) and physical layer (PHY) specifications: enhance-ments for very high throughput for operation in bands below 6 GHz [EB/OL]. (2012)[2012-05].http://ieeexplore.ieee.org/xpl/standards.jsp.
[2]Bianchi G. Performance analysis of the IEEE 802.11 distributed coordination function[J].IEEEJournalonSelectedinCommunications, 2000,18(3):535-547.
[3]Nguyen H Q, Baccelli F, Kofman D. A stochastic geometry analysis of dense IEEE 802.11 networks[C]//IEEE26thInternationalConferenceonComputerCommunications. Anchorage, AK,USA, 2007:1199-1207.
[4]Ge X H, Huang K, Wang C X, et al. Capacity analysis of a multi-cell multi-antenna cooperative cellular networks with co-channel interference [J].IEEETransactiononWirelessCommunications, 2012,10(10):3298-3309.
[5]Win M Z, Pinto P C. A mathematical theory of network interference and its applications[J].IEEEProceedings, 2009,97(2):205-230.
[6]Shao X, Yuan J, Shao Y. Error performance analysis of linear zero forcing and MMSE precoders for MIMO broad-cast channels [J].IETCommunications, 2007,1(5): 1067-1074.
[7]Gradshteyn I S, Ryzhik I M.Tableofintegrals,series,andproducts[M]. 7th ed. San Diego, CA,USA: Academic, 2000.
[8]Salbaroli E, Pertropulu A. Interference analysis in a poisson field of nodes of finite area [J].IEEETransactiononVehicleTechnology, 2009,58(4):1776-1883.
[9]Prudnikov A P, Brychkov Y A, Marichev O I.Integralsandseries[M]. Moscow, Russia: Gordon and Breach Science, 1986.
[10]Wang Z, Giannakis G B. A simple and general parameterization quantifying performance in fading channels [J].IEEETransactionsonCommunications, 2003,51(8):1389-1398.
[11]Yury A, Brychkov Y A.Handbookofspecialfunctions,derivatives,integrals,seriesandotherformulas[M]. Moscow, Russia: CRC Press, 2008.

